1. Introduction
The group of materials with ABO3 type perovskite structure is also very important due to their attractive electrical and magnetic properties for technological applications and richness of physical and chemical aspects they possess. The perovskite lead zirconate titanate Pb (ZrxTi1−x)O3 abbreviated as PZT is known to have excellent piezoelectric properties and used as transformers, ultrasonic motors and electromechanical transducers; it is desirable to combine high mechanical quality factor (Qm) with large coupling factor (kp) and low dielectric loss as well as high mechanical strength [1] -[3] . Relaxors are mainly lead-based perovskite solid solutions and exhibit a stronger piezoelectric effect, high permittivity over a broad temperature range, unique dielectric response with strong frequency dispersion, and anomalous phonon dispersion relation [4] -[6] . Relaxors are used in transducers and capacitors due to the excellent dielectric and piezoelectric properties. As like, prototypical (1-x)Pb(Mg1/3,Nb2/3)O3 relaxors form the core of the state-of-the-art ultrasound medical imaging probes. However, in SONAR transducers, conventional crystalline PZT is widely used despite the fact that relaxors show about four to ten times larger the d33 coefficients. This is due to loss of piezoelectric performance below unsuitably low Curie temperature and low coercive fields in the relaxors compared with PZT. The diffusive and dispersive characteristics of the inverse dielectric response are signatures of relaxor behavior. The diffuse phase transitions that take place gradually are called relaxed phase transitions, giving rise to the term “relaxor”. Currently, experimental and theoretical investigations of relaxors are ongoing due to the technological applications and scientific interest of the modified PZT materials [7] -[9] .
These compositional modifications may be incorporated either by chemical substitution at A-sites or B-sites of the perovskite structure or by using off-valent element as an additive. In the miniaturization era of technological advancement, there is ever a pressing need for light, efficient, reliable, and long lasting devices for power supply. This requires new generation of electric components like transformer, capacitor, transistor etc. The most commonly used tiny piezoelectric transformers are based on PT and PZT compositions. The hard and soft PZTs have their own advantages. The former has a low dielectric loss factor and a high mechanical quality factor (Qm) while the latter has a high piezoelectric constant and a high coupling coefficient. Usually hard piezoelectric ceramics are found to be useful for transformer applications, because of their high mechanical quality factor (Qm) [10] -[13] . Modified PZT ceramics have found applications in high power and transmitting components which demand high mechanical, dielectric and piezoelectric properties. In order to obtain proper ceramics which combine the advantages of both hard and soft PZTs, different modifications have been investigated. Mn2+ like Fe3+ is generally known as hard additive to generate O2− vacancies. Sr2+ cation replaces Pb2+ on the A-site. In the same way, Mn2+ cation replaces Zr4+ or Ti4+ on the B-site. O-site vacancies lead to contraction of the grain body. In this paper, we have therefore concentrated on a hard piezoelectric ceramic composition [Pb0.94Sr0.06] [(Mn1/3Sb2/3)0.05(Zr0.49Ti0.51)0.95]O3 as a case study to examine the phenomenon and mechanisms of dielectric relaxation. It is also known that the piezoelectric properties of Sr2+ substituted PZT are most pronounced for x = 0.06. However, no attempt has so for been made to prepare 6% Sr2+ substituted PZT ceramics with lead manganese antimonite as an additional hardener dopant. The present work aims to fill this gap. The distribution of relaxation times [13] -[15] will be confirmed by Cole-Cole plots and scaling behavior of imaginary part of the electric modulus. The frequency-dependent electrical data will also be analyzed in the framework of the conductivity and modulus formalisms.
2. Experimental
Stoichiometric amounts of the PbCO3 and SrCO3 powders were taken for the preparation of [Pb0.94Sr0.06]CO3. Saturated solution of ammonium carbonate was added in the solution of PbCO3 and SrCO3 in dilute nitric acid to obtain the precipitate of [Pb0.94Sr0.06]CO3. The precipitate was washed with distilled water until ammonia was removed and then dried in an oven. Now stoichiometric amounts of Sb2O5 (99% purity) and MnCO3 (99.9% purity) were mixed with the help of mortar and pestle for 6 hours to obtain the intimate mixture. In order to obtain the preparation of the final composition [Pb0.94Sr0.06][(Mn1/3Sb2/3)0.05(Zr0.49Ti0.51)0.95]O3, the stoichiometric amounts of [Pb0.94Sr0.06]CO3, and manganese antimonite (MnSb2O6), ZrO2 (99% purity) and TiO2 (99.5% purity) were mixed with the help of mortar and pestle for 6 hours to get an intimate homogeneous mixture. This mixture was dried in air and then calcined at 800˚C for 6 hours. Heat treatments involving calcinations and sintering (1170˚C) were carried out with the help of a high temperature Globar furnace. Sintering was performed in PbO atmosphere to avoid lead loss. In the present work, the pellets were sintered in PbO environment created by lead zirconate as a spacer powder in a covered alumina crucible using MgO powder as a sealing agent. This arrangement reduces the lead oxide losses at higher sintering temperature effectively. The duration of calcinations (800˚C) and sintering (1170˚C) each was kept for 6 hours. The powder compaction was done using a cylindrical die of 8 mm diameter and a hydraulic press. Before cold compaction of calcined powder, a few drops of 2% PVA aqueous solution were added to serve as a binder. For the electrical characterizations, the sintered ceramic pellets were electroded using the silver paste. After applying the paste the pellets were then dried at about 150˚C in an oven. The silver paste coated pellets were fired at 500˚C for five minutes. The room temperature dielectric measurements of these electroded pellets were done using Hioki LCR meter.
3. Rietveld Refinement Details
Rietveld refinement was carried out using the XRD data with the help of the DBWS-9411 program [9] . The background was fitted with 6-Cofficients polynomials function, while the peak shapes were described by pseudo-Voigt profiles. In all the refinements, scale factor, lattice parameters, positional coordinates (x, y, z) and thermal parameters were varied. Occupancy parameters of all the ions were kept fixed during refinement. No correlation between the positional and thermal parameters was observed during refinement and as such it was possible to refine all the parameters together.
4. Results and Discussion
Figure 1 shows the XRD patterns of the pure perovskite phase of [Pb0.94Sr0.06][(Mn1/3Sb2/3)0.05(Zr0.49Ti0.51)0.95]O3 ceramics. All the reflection peaks of the X-ray profile are indexed. As shown in the inset of Figure 2, the magnified Bragg profiles of the {200}c and {111}c pseudocubic reflections. From virtual inspection of the shape of Bragg’s profile we noted that the {200}c is split into two and {111}c is singlet. This is compatible with a tetragonal (P4mm) structure. The Pb2+/Sr2+ ions occupy 1 (a) sites at (0, 0, z), Mn2+/Sb5+/Zr4+/Ti4+ and 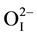 occupy 1 (b) sites at (1/2, 1/2, z), and
occupy 1 (b) sites at (1/2, 1/2, z), and 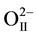 occupy 2(c) sites at (1/2, 0, z). For the refinement, the initial values of the lattice parameters were obtained from our XRD data by least squares method, whereas the values of the structural parameters were taken from Noheda et al. [16] [17] . In this structure, Pb2+/Sr2+ coordinates were fixed at (0, 0, 0) in our refinement. Figure 2 also depicts the observed, calculated and difference profiles for the refined structure. The fit is quite good. The refined structural parameters and the positional coordinates of this composition are given in Table 1. SEM studies (Figure 3) carried out on the sintered specimens reveal that the average grain size is 7.5 µm with homogenous structures and well-grown grains having a sharp grain boundary. The angular frequency
occupy 2(c) sites at (1/2, 0, z). For the refinement, the initial values of the lattice parameters were obtained from our XRD data by least squares method, whereas the values of the structural parameters were taken from Noheda et al. [16] [17] . In this structure, Pb2+/Sr2+ coordinates were fixed at (0, 0, 0) in our refinement. Figure 2 also depicts the observed, calculated and difference profiles for the refined structure. The fit is quite good. The refined structural parameters and the positional coordinates of this composition are given in Table 1. SEM studies (Figure 3) carried out on the sintered specimens reveal that the average grain size is 7.5 µm with homogenous structures and well-grown grains having a sharp grain boundary. The angular frequency 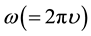 dependent plots of the real (ε') and imaginary (ε") parts of complex dielectric permittivity (ε⋆) of the given composition at several temperatures from room temperature (303 K) to 775 K are shown in Figure 4. A relaxation is observed in the entire temperature range as a gradual decrease in ε'(ω) and as a broad peak in ε"(ω). Relaxation phenomena in dielectric materials are associated with a frequency-dependent orientational polarization. At low frequency, the permanent dipoles align themselves along the field and contribute fully to the total polarization of the dielectric. At higher frequency, the variation in the field is too rapid for
dependent plots of the real (ε') and imaginary (ε") parts of complex dielectric permittivity (ε⋆) of the given composition at several temperatures from room temperature (303 K) to 775 K are shown in Figure 4. A relaxation is observed in the entire temperature range as a gradual decrease in ε'(ω) and as a broad peak in ε"(ω). Relaxation phenomena in dielectric materials are associated with a frequency-dependent orientational polarization. At low frequency, the permanent dipoles align themselves along the field and contribute fully to the total polarization of the dielectric. At higher frequency, the variation in the field is too rapid for
![]()
Figure 1. XRD pattern of powder at room temperature.
![]()
Figure 2. Rietveld fit of the X-ray powder diffraction of the given composition. The dot represent the observed data, the continuous line is the fitted pattern, the vertical bars show the Bragg peak position. The arrows highlight the pseudocubic {111}pc and {200}pc Bragg profiles.
![]()
Figure 3. Scanning electron micrographs of sintered composition.
![]()
Table 1. Refined structural parameters of [Pb0.94Sr0.06][(Mn1/3Sb2/3)0.05(Zr0.49Ti0.51)0.95]O3 using tetragonal (space group; P4mm) model.
![]()
Figure 4. Frequency dependence of the (a) ε' and (b) tanδ of the material at various temperatures.
the dipoles to align themselves, so their contribution to the polarization and hence to the dielectric permittivity can become negligible. Therefore the dielectric permittivity ε'(ω) decreases with increasing frequency. It is evident from Figure 3(b) that the peak position of ε" (centered at the dispersion region of ε') shifts to higher frequency with increasing temperature and that a strong dispersion of ε″ exists in present material. The increase in the peak value of ε″ with the increase in temperature indicates an increase in charge carriers in given material by thermal activation (showing the semiconducting behavior of the sample). It is evident that the width of the loss peaks in Figure 3(b) cannot be accounted for in terms of a monodispersive relaxation process but points towards the possibility of a distribution of relaxation times. If g(τ, T) is the temperature dependent distribution function for relaxation time, the complex dielectric constant can be expressed as [18] -[21]
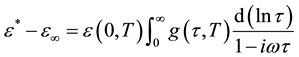 , (1)
, (1)
giving
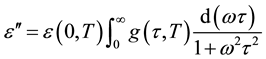 , (2)
, (2)
where  is the low-frequency dielectric constant. Thus, the spectrum of dielectric loss gives direct information about
is the low-frequency dielectric constant. Thus, the spectrum of dielectric loss gives direct information about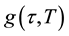 . One of the most convenient ways of checking the polydispersive nature of dielectric relaxation is through complex Argand plane plots between ε″ and ε', usually called Cole-Cole plots [22] [23] . For a pure monodispersive Debye process, one expects semicircular plots with a centre located on the ε' axis, whereas, for polydispersive relaxation, these Argand plane plots are close to circular arcs with end points on the axis of real and a centre below this axis. The complex dielectric constant in such situations is known to be described by the empirical relation
. One of the most convenient ways of checking the polydispersive nature of dielectric relaxation is through complex Argand plane plots between ε″ and ε', usually called Cole-Cole plots [22] [23] . For a pure monodispersive Debye process, one expects semicircular plots with a centre located on the ε' axis, whereas, for polydispersive relaxation, these Argand plane plots are close to circular arcs with end points on the axis of real and a centre below this axis. The complex dielectric constant in such situations is known to be described by the empirical relation
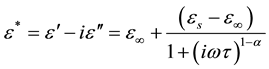 (3)
(3)
where εs and ε∞ are the low- and high-frequency values of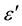 , respectively, and α is a measure of the distribution of relaxation times. The parameter α can be determined from the location of the centre of the Cole-Cole circles of which only an arc lies above the
, respectively, and α is a measure of the distribution of relaxation times. The parameter α can be determined from the location of the centre of the Cole-Cole circles of which only an arc lies above the 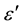 -axis. Figure 4(a) and Figure 4(b) depict two such representative plots for T = 313 K and 423 K. It is evident from these plots that the relaxation process differs from the monodispersive Debye process (for which α = 0). The parameter α, as determined from the angle subtended by the radius of the circle with the ε' axis passing through the origin of the
-axis. Figure 4(a) and Figure 4(b) depict two such representative plots for T = 313 K and 423 K. It is evident from these plots that the relaxation process differs from the monodispersive Debye process (for which α = 0). The parameter α, as determined from the angle subtended by the radius of the circle with the ε' axis passing through the origin of the 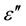 axis, shows a very small increase in the interval (0.56, 0.66) with the decrease of temperature from 423 K to 313 K, implying a slight increase in the distribution of the relaxation time with decreasing temperature.
axis, shows a very small increase in the interval (0.56, 0.66) with the decrease of temperature from 423 K to 313 K, implying a slight increase in the distribution of the relaxation time with decreasing temperature.
The Cole-Cole plots confirm the polydispersive nature of dielectric relaxation of the titled material. However the small variation in α with decreasing temperature is not convincing enough, keeping in mind the uncertainties in fitting the circle, which was done through a visual fit to the observed data points. Figure 5 and Figure 6 are shown the variation of dielectric constants (real and imaginary parts) with frequencies (100 Hz - 1 MHz) at different temperatures (303 K - 583 K). The real part of the dielectric constant is found to decrease with increasing frequency at different temperatures while the position of dielectric loss peak shifts to higher frequencies with increasing temperature indicating a strong dispersion beyond the transition temperature, a feature known for relaxational systems such as dipole glasses. The magnitude of dielectric constant decreases with increasing frequency which is a typical characteristic of ferroelectric material. It is evident from Figure 5 that the position of the loss peak shifts to higher frequencies with increasing temperature and that a strong dispersion of ![]() exists similar to what is known for relaxational systems such as dipole glasses [24] . At temperature far above Tm in two frequencies (100 Hz & 1 KHz) a monotonous increase in the value of
exists similar to what is known for relaxational systems such as dipole glasses [24] . At temperature far above Tm in two frequencies (100 Hz & 1 KHz) a monotonous increase in the value of ![]() caused by electrical conduction is observed. The frequency dependence of
caused by electrical conduction is observed. The frequency dependence of ![]() and
and ![]() for our material at various temperatures is shown in Figure 7.
for our material at various temperatures is shown in Figure 7. ![]() show a dispersion tending toward M∞ (the asymptotic value of
show a dispersion tending toward M∞ (the asymptotic value of ![]() at higher frequencies (Figure 7(a)), while
at higher frequencies (Figure 7(a)), while ![]() exhibits a maximum
exhibits a maximum ![]() (Figure 7(b)) centered at the dispersion region of
(Figure 7(b)) centered at the dispersion region of![]() . It may be noted from Figure 7(b) the frequency region below peak maximum
. It may be noted from Figure 7(b) the frequency region below peak maximum ![]() determines the range in which charge carriers are mobile on long distances. At frequencies above peak maximum, the carriers are confined to potential wells, being mobile on short distances. The value of
determines the range in which charge carriers are mobile on long distances. At frequencies above peak maximum, the carriers are confined to potential wells, being mobile on short distances. The value of ![]() increases with increasing temperature though slightly and shifts to the higher frequency side. At any temperature T, the most probable relaxation time corresponding to the peak position in tanδ versus lnω and M″ versus lnω is proportional to exp (−Ea/kBT) (Arrhenius law) with activation energies ≈ 0.15 and 0.21 eV, respectively, as shown in Figure 8. Such a value of activation energy indicates that the conduction mechanism for present material may be due to the polaron hopping based on the electron carriers. In the hopping process, the electron disorders its surroundings by moving its neighboring atoms from their equilibrium positions, causing structural defects in the B perovskite sites of the system.
increases with increasing temperature though slightly and shifts to the higher frequency side. At any temperature T, the most probable relaxation time corresponding to the peak position in tanδ versus lnω and M″ versus lnω is proportional to exp (−Ea/kBT) (Arrhenius law) with activation energies ≈ 0.15 and 0.21 eV, respectively, as shown in Figure 8. Such a value of activation energy indicates that the conduction mechanism for present material may be due to the polaron hopping based on the electron carriers. In the hopping process, the electron disorders its surroundings by moving its neighboring atoms from their equilibrium positions, causing structural defects in the B perovskite sites of the system.
We have scaled each M″ by ![]() and each frequency by ωmax, where ωm corresponds to the frequency of the peak position of M″ in the M″ versus lnω plots in Figure 9. The overlap of the curves at different temperatures
and each frequency by ωmax, where ωm corresponds to the frequency of the peak position of M″ in the M″ versus lnω plots in Figure 9. The overlap of the curves at different temperatures
![]()
Figure 5. Cole-cole plot at (a) 313 K and (b) 423 K.
![]()
Figure 6. Temperature dependence of the (a) ε' and (b) ε" of the material at various frequencies.
![]()
Figure 7. Frequency dependence of the (a) M' and (b) M" of the material at various temperatures.
![]()
Figure 8. The Arrhenius plot of ωm corresponding to tanδ and corresponding to M'.
![]()
Figure 9. Scalling behavior of M" at various temperatures for the given composition.
into a single master curve indicates that the relaxation describes the same mechanism at various temperatures. Figure 10 shows the frequency dependence of the ac conductivity σ(ω) for given composition at different measuring temperaturs. The conductivity shows a dispersion which shifts to higher frequencies with an increase in temperature. In Figure 11, the variations of the normalized parameter ![]() and tanδ/tanδmax as a function of logarithmic frequency measured at 403 K for present material are shown. For delocalized or long range conduction, the peak position of two curves should overlap [25] [26] . However, for the present system, the
and tanδ/tanδmax as a function of logarithmic frequency measured at 403 K for present material are shown. For delocalized or long range conduction, the peak position of two curves should overlap [25] [26] . However, for the present system, the ![]() and tanδ/tanδmax peaks do not overlap, suggesting the components from both long range and localized relaxation. In order to mobilize the localized electron, the aid of lattice oscillation is required. In these circumstances, electrons are considered not to move by themselves but by hopping motion activated by lattice
and tanδ/tanδmax peaks do not overlap, suggesting the components from both long range and localized relaxation. In order to mobilize the localized electron, the aid of lattice oscillation is required. In these circumstances, electrons are considered not to move by themselves but by hopping motion activated by lattice
![]()
Figure 10. Frequency spectra of the conductivity for the given composition at various temperatures.
![]()
Figure 11. Frequency dependence of normalized peaks, ![]() and tanδ/tanδmax at 403 K.
and tanδ/tanδmax at 403 K.
oscillation, i.e., the conduction mechanism should be considered as phonon-assisted hopping of small polaron between localized states. In addition, the magnitude of the activation energy suggests that the carrier transport is due to the hopping conduction.
5. Conclusion
The frequency dependent dielectric relaxation and conductivity of the [Pb0.94Sr0.06][(Mn1/3Sb2/3)0.05(Zr0.49Ti0.51)0.95] ceramics synthesized by a solid-state reaction technique are investigated in the temperature range from 313 to 773 K. The SEM of the sample also confirms the formation of single phase of the material. The frequency dependence of the loss peak is found to obey an Arrhenius law with activation energy of 0.15 eV. This value of activation energy suggests that the bulk conduction in present material may be due to polaron hopping based on the electron carriers. The distribution of relaxation times is confirmed by Cole-Cole plots. The frequency-de- pendent electrical data are also analyzed in the framework of the conductivity and modulus formalisms. These formalisms yield qualitative similarities in the relaxation times. The presence of peak in the temperature dependence of the imaginary part of the dielectric constant ![]() indicates that the hopping of charge carriers is responsible for the dielectric relaxation. The scaling behavior of the imaginary part of the electric modulus
indicates that the hopping of charge carriers is responsible for the dielectric relaxation. The scaling behavior of the imaginary part of the electric modulus ![]() suggests that the relaxation describes the same mechanism at various temperatures. In conclusion, we have thus here confirmed the polydispersive nature of dielectric relaxation of the present composition through the Cole-Cole plots. We have also used the conductivity as well as the modulus formalism to settle the relaxation mechanisms in the present material.
suggests that the relaxation describes the same mechanism at various temperatures. In conclusion, we have thus here confirmed the polydispersive nature of dielectric relaxation of the present composition through the Cole-Cole plots. We have also used the conductivity as well as the modulus formalism to settle the relaxation mechanisms in the present material.
NOTES
*Corresponding author.