A Study of Heavy-Fermion Superconductors via BCS Equations Incorporating Chemical Potential ()
1. Introduction
Heavy-fermion superconductors (HFSCs) [1] belong to a fascinating family of compounds which can also be found in a variety of other states such as metallic, insulating and magnetic. HFSCs are so called because a conduction electron in them behaves as if it has an effective mass up to three orders of magnitude greater than its free mass. Superconductivity in these compounds was discovered by Steglich et al. [2] ; since then it has been authoritatively dealt with, e.g., in [3] and [4] .
Some remarkable features of HFSCs are [5] :
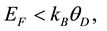 (1a)
(1a)
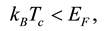 (1b)
(1b)
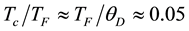 (1c)
(1c)
where EF, θD, Tc, and TF denote, respectively, the Fermi energy, Debye temperature, critical temperature and Fermi temperature of the SC, and kB is the Boltzmann constant.
Note in particular that Inequality (1a) is in conflict with the following basic assumption of BCS theory
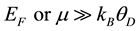 , (2)
, (2)
where μ is the chemical potential. Therefore, despite their rather low Tcs, HFSCs are regarded as outside the purview of the usual BCS equations. This feature―at least partly―is responsible for coinage of the term exotic or unconventional for them.
HFSCs are characterized by two additional distinguishing features that have a bearing on the pairing mechanism operative in them. These are: 1) large heat capacities of conduction electrons―much larger than those found for the elemental SCs and as large as those usually associated with fixed magnetic momenta, and 2) anisotropy of their gap-structures. These features naturally led to the revival of an old idea that superconductivity may also arise without the mediating role of phonons. Thus, with He-3 in mind, triplet pairing was initially regarded as the cause of superconductivity in these SCs. However, it was subsequently shown in three well-known papers [6] -[8] that several experimental features of HFSCs can be explained if one assumes that magnetic fluctuations are the cause of d-wave pairing in them. By and large, this currently seems to be the popular view.
The study undertaken here is not in a spirit of dissension with the above view. Rather, it is motivated by the question: does the “popular” view definitively exclude all other mechanisms of pairing? We believe it does not because HFSCs are materials that exhibit multi-phase, multi-scale complexity. These features―together with the fact that at least one of such SCs, namely UPt3, is already known to undergo more than one phase transition―suggest that an HFSC may well be characterized by different forms of pairing mechanisms in different parts of momentum space. This is a scenario inspired by the multi-condensate superconductivity approach advocated by Bianconi and collaborators ([9] , and references therein). We now recall that a case has been made for the applicability of the electron-lattice interactions to a wide variety of SCs [10] ; also that by employing such interactions, the Tcs and multiple gaps of several high-Tc SCs have been accounted for via the generalized BCS equations [11] -[14] . Note that complexity of structure is a feature common to both high-Tc SCs and HFSCs.
Guided by above considerations, we assume here that itinerancy of conduction electrons and hybridzation of orbitals in an HFSC can cause them to be in a region of momentum space where, effectively, pairing is via an s-wave electron-lattice interaction. In order then to deal quantitatively with an HFSC, we need equations for its Tc and ∆0 (the gap at T = 0) that are not constrained by Inequality (2), i.e., equations that contain μ as a variable. Such equations, which are in fact an integral part of BCS theory, have been available since at least the time of [15] concerned with BCS-BEC crossover physics. A feature of these equations that seems to us to have escaped serious attention is: after suitable modification as discussed below, they can also be employed to shed light on real life SCs such as HFSCs.
This paper is organized as follows. In the next section we present the μ-incorporated equations for ∆0 and Tc― equations which are variants of those considered in [15] and were recently obtained in studies concerned with 1) crossover physics without appeal to scattering length theory [16] and 2) a long-standing puzzle posed by superconducting SrTiO3 [17] . Since these equations have a greater range of applicability than the usual equations sans μ, they may be regarded as comprising an extended form of BCS theory. In the following we shall therefore refer to them collectively as ET―extended (BCS) theory. ET is applied in Section 3 (4) to a prominent member of the HFSC family, namely CeCoIn5, by assuming that pairing in it is caused by Ce(Co) ions. Section 5 deals with densities of the charge carriers that our study leads to. This is followed up by a detailed discussion of our approach and a succinct summing up.
2. ET: BCS Equations Incorporating Chemical Potential
BCS equation for ∆0 and Tc incorporating μ were obtained in [17] as:
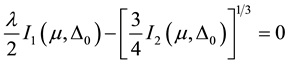 (3)
(3)
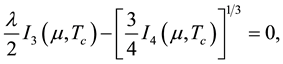 (4)
(4)
where
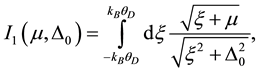 (5)
(5)
 (6)
(6)
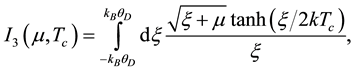 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10a)
(10a)
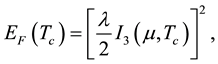 (10b)
(10b)
and V (as in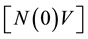 ) is a term due to both Coulomb repulsion between a pair of electrons and attraction between them because of the ion-lattice. It is easily seen that Equations (3) and (4) go over to the usual BCS equations for ∆0 and Tc, respectively, when Inequality (2) is imposed.
) is a term due to both Coulomb repulsion between a pair of electrons and attraction between them because of the ion-lattice. It is easily seen that Equations (3) and (4) go over to the usual BCS equations for ∆0 and Tc, respectively, when Inequality (2) is imposed.
Equations (3) and (4) have been written here―unlike in [17] ―by assuming that
 (11)
(11)
where sub-scripts 0 and 1 denote values of a symbol at T = 0 and T = Tc, respectively. Strictly speaking, i.e., to be perfectly general, distinction should be made between V0 and V1, as also between values of each of the other two variables at the two temperatures. However, as was pointed out in [17] , on doing so one is led to an undetermined set of equations. We recall that neither V nor μ is required for the calculation of either ∆0 or Tc via the usual BCS equations―for both of which λ has the same value. Therefore, as a matter of fact, the final subset of equalities in the set of Equations (11) is in accord with a tenet of the BCS theory.
An important feature of ET is that its expressions for![]() ,
, ![]() and
and ![]() given by Equations (5), (6) and (7), respectively, lead to complex values when μ < kBθD. Real solutions can however still be obtained by replacing the lower limit (−kBθD) in each of these equations by ?μ. It is in this sense that the word modification was used above. While the issue of such solutions will be further discussed below, we shall henceforth refer to any equation with curtailed limits as a truncated equation.
given by Equations (5), (6) and (7), respectively, lead to complex values when μ < kBθD. Real solutions can however still be obtained by replacing the lower limit (−kBθD) in each of these equations by ?μ. It is in this sense that the word modification was used above. While the issue of such solutions will be further discussed below, we shall henceforth refer to any equation with curtailed limits as a truncated equation.
3. Application of ET to CeCoIn5: Pairing via the Sub-Lattice Containing Ce Ions
We now apply ET to CeCoIn5 which has the highest Tc in its family. Its characteristic features of immediate concern to us are:
![]() [18] ;
[18] ; ![]() [19] . (12)
[19] . (12)
It follows from the structure of CeCoIn5 that, in the one-phonon exchange scenario, pairing in it can be caused by either of Ce and Co ions. We first consider Ce ions.
3.1. Debye Temperature of Ce Ions
Assuming that θD of the CeIn3 layers is 161 K, we can calculate θDs of the Ce and the In ions―which must be different because their masses are different. That an anisotropic material may be characterized by more than one Debye temperature is an idea that dates back to Born and Karmann―it was given in the context of a modification of the Debye theory of specific heat of such materials. A review of this body of work and references to it can be found in [20] .
![]() and
and ![]() can be calculated via the following equations applied to the In3Ce layer
can be calculated via the following equations applied to the In3Ce layer
![]() (13)
(13)
![]() (14)
(14)
The first of the above equations has routinely been used for binaries represented by AxB1−x; the second is obtained by assuming that the constituents of a binary simulate weakly coupled oscillations of a double pendulum. A derivation of Equation (14) has been given in [11] . Note that Equations (13) and (14) have been written by assuming that Ce is the lower of the two bobs.
With![]() ,
, ![]() and
and![]() , we obtain
, we obtain
![]() . (15a)
. (15a)
The assumption that Ce is upper of the two bobs in the double pendulum leads to
![]() . (15b)
. (15b)
In the following we shall perform all calculations with both the values of θD(Ce) noted in Equations (15a) and (15b).
3.2. A Consistency Check of Equations (3) and (4)
In dealing with CeCoIn5, keeping Inequality (1a) in view, we need to solve Equations (3) and (4) for![]() . Before we do so, as a consistency check, we solve these equations for a value of μ that satisfies Inequality (2).
. Before we do so, as a consistency check, we solve these equations for a value of μ that satisfies Inequality (2).
Choosing![]() ―which manifestly satisfies Inequality (2)―and using as input Tc = 2.3 K and
―which manifestly satisfies Inequality (2)―and using as input Tc = 2.3 K and ![]() into Equation (4), we obtain λ = 0.2788. Employing these values of μ,
into Equation (4), we obtain λ = 0.2788. Employing these values of μ, ![]() and λ as input, solution of Equation (3) then gives ∆0 = 3.50 × 10−4 eV. Upon solving the usual BCS equations―which do not require the input of μ―these are also the values for λ and ∆0 that we obtain for the same values of Tc and
and λ as input, solution of Equation (3) then gives ∆0 = 3.50 × 10−4 eV. Upon solving the usual BCS equations―which do not require the input of μ―these are also the values for λ and ∆0 that we obtain for the same values of Tc and![]() . Changing
. Changing ![]() to 276.3 K changes the value of λ to 0.2035, without affecting the earlier value of ∆0. These results, i.e., the values of λ and ∆0, are also obtained by solving the usual BCS equations with the same inputs (Tc = 2.3 K, θD(Ce) = 276.3 K).
to 276.3 K changes the value of λ to 0.2035, without affecting the earlier value of ∆0. These results, i.e., the values of λ and ∆0, are also obtained by solving the usual BCS equations with the same inputs (Tc = 2.3 K, θD(Ce) = 276.3 K).
All results of the preceding paragraph remain valid for values of μ greater than![]() . It is hence seen that, when Inequality (2) is imposed, the μ-incorporated Equations (4) and (3) yield solutions in accord with solutions of the usual BCS equations―as was to be expected.
. It is hence seen that, when Inequality (2) is imposed, the μ-incorporated Equations (4) and (3) yield solutions in accord with solutions of the usual BCS equations―as was to be expected.
3.3. Solutions of Equations (4) and (3) with the Input of θD(Ce) = 73.3 K, Tc = 2.3 K, and Different Values of μ
Combining Inequalities (1a) and (1b), we obtain
![]() . (16)
. (16)
We now solve Equations (4) and (3) for a range of μ that marginally exceeds the one specified by Inequalities (16), i.e., ![]() (6.632 × 10−3 ≥ μ ≥ 1.883 × 10−4 eV). This is done in order to bring out the change that occurs when μ is lowered across kBθD. For decreasing values of μ, we proceed as follows:
(6.632 × 10−3 ≥ μ ≥ 1.883 × 10−4 eV). This is done in order to bring out the change that occurs when μ is lowered across kBθD. For decreasing values of μ, we proceed as follows:
(a) Solve Equation (4) for λ beginning with μ = 1.05kBθD.
(b) Solve Equation (3) for ∆0 with the input of (μ, λ) values from (a).
(c) Repeat the above steps for μ = kBθD.
(d) Repeat steps (a) and (b) for values of μ < kBθD. Upon attempting to do so, Equations (5), (6) and (7) are found to lead to complex-valued expressions because of the factor ![]() in each one of them. Hence, as was pointed out earlier, real solutions are now obtained via truncated equations.
in each one of them. Hence, as was pointed out earlier, real solutions are now obtained via truncated equations.
(e) Repeat steps (a) and (b) for 13 values of μ in the range ![]() by employing truncated equations.
by employing truncated equations.
The results of these calculations have been shown in the plots of λ and ∆0 against μ in Figure 1 and Figure 2, respectively. For convenience of the reader, numerical values corresponding to four special points in these figures have been given in Table 1. These points are 1) μ = kBθD (6.317 meV), i.e., the end-point on the LHS of Inequality (16), 2) the point corresponding to apex of the μ vs. λ plot, i.e., μ ≈ 0.3 kBθD (1.895 meV), 3) the point where ![]() (see Equation (1c)), i.e., μ = 1.119 meV, and 4) μ = kBTc (1.982 × 10−4 eV), i.e., the end-point on the RHS of Inequality (16). Corresponding to each pair of (λ, ∆0) values in Table 1 are also given values of EF(0) and EF(Tc) which are obtained via Equations (10a) and (10b), respectively.
(see Equation (1c)), i.e., μ = 1.119 meV, and 4) μ = kBTc (1.982 × 10−4 eV), i.e., the end-point on the RHS of Inequality (16). Corresponding to each pair of (λ, ∆0) values in Table 1 are also given values of EF(0) and EF(Tc) which are obtained via Equations (10a) and (10b), respectively.
3.4. Effective Mass of Conduction Electrons
Given the value of![]() , the effective mass of conduction electrons can be calculated by appealing to two alternative expressions for
, the effective mass of conduction electrons can be calculated by appealing to two alternative expressions for![]() . One of these, as seen from Equation (9), is:
. One of these, as seen from Equation (9), is:
![]() (17)
(17)
where we have put the band effective mass as s times the free electron mass me.
Another expression [21] for ![]() is
is
![]()
Figure 1. For pairing via the sub lattice containing Ce ions, plot of λ vs. μ obtained by solving Equation (4) with the input of θD = 73.3 K and Tc = 2.3 K for DECREASING values of μ in the range 1.05kBθD ≥ μ ≥ 0.95kBTc.
![]()
Figure 2. For pairing via the sub lattice containing Ce ions, plot of ∆0 vs. μ obtained by solving Equation (3) corresponding to values of θD, μ, and λ in Figure 1.
![]()
Table 1. For pairing via Ce ions, values of λ obtained by solving truncated Equation (4) for four select values of μ with the input of Tc = 2.3 K and two values of θD, i.e., 73.3 K and 276.3 K. Values of (μ, λ) in each row are then used to calculate ∆0, EF(0), and EF(Tc) via Equations (3), (10a), and (10b), respectively. The values of s are obtained by using Equation (24).
![]() (18)
(18)
where γ is the experimentally obtained electronic specific heat constant (also known as the Sommerfeld constant) and v the gm-at volume. From Equations (17) and (18) we obtain
![]() (19)
(19)
The values of γ and v(Ce) required to calculate s are:
![]() . (20)
. (20)
Using Equations (19) and (20), the values of s obtained for the four special points in the λ vs. μ plot in Figure 1 that were mentioned above have also been included in Table 1.
3.5. Solutions of Equations (4) and (3) with the Input of θD(Ce) = 276.3 K, Tc = 2.3 K, and Different Values of μ
Combining Inequalities (1a) and (1b), we now have
![]() . (21)
. (21)
As we did when ![]() was 73.3 K, we solve Equations (4) and (3) for 15 values of μ in the range 1.05kBθD ≥ μ ≥ 0.95kBTc (25.0 × 10−3 ≥ μ ≥ 1.883 × 10−4 eV), which marginally exceeds the range given by Inequalities (21). Since the plots of λ and ∆0 against μ now are similar to those shown in Figure 1 and Figure 2, respectively, they are not shown here. However, we have included in the lower part of Table 1 all the results akin to those that were given in upper part of the table for
was 73.3 K, we solve Equations (4) and (3) for 15 values of μ in the range 1.05kBθD ≥ μ ≥ 0.95kBTc (25.0 × 10−3 ≥ μ ≥ 1.883 × 10−4 eV), which marginally exceeds the range given by Inequalities (21). Since the plots of λ and ∆0 against μ now are similar to those shown in Figure 1 and Figure 2, respectively, they are not shown here. However, we have included in the lower part of Table 1 all the results akin to those that were given in upper part of the table for![]() .
.
4. Application of ET to CeCoIn5: Pairing via with the Sub-Lattice Containing Co Ions
We have so far considered the effects of pair-formation via the Ce ions. On repeating the above exercise with Co ions, we find that θD(Co) = 98.7 K in In2Co layers, i.e., when Co is lower of the two bobs in the double pendulum; otherwise θD(Co) = 294.1 K (in CoIn2 layers). On now solving Equations (4) and (3), the plots of λ and ∆0 against μ are found to be similar to those obtained earlier and hence are not included here. Given in Table 2 are all the other results akin to those that were given in Table 1 for pairing via the Ce ions. We note that the value of v(Co) is 6.67 cm3, which differs considerably from that of v(Ce) given in Equation (20).
5. Density of Charge Carriers
Density of charge carriers, n, is an important parameter for any SC. It is given by
![]() (22)
(22)
![]()
Table 2. For pairing via Co ions, values of λ obtained by solving truncated Equation (4) for four select values of μ with the input of Tc = 2.3 K and two values of θD, i.e., 98.7 K and 294.7 K. Values of (μ, λ) in each row are then used to calculate ∆0, EF(0), and EF(Tc) via Equations (3), (10a), and (10b), respectively. The values of s in the last column are obtained by using Equation (24).
In this equation m is to be taken as s times the free electron mass. The results for n following from the s and ![]() values given in the two tables are as follows:
values given in the two tables are as follows:
For pairing via the Ce ions:
![]()
For pairing via the Co ions:
![]()
6. Discussion
Based on experiments performed by employing the Bogoliubov quasi-particle interference (QPI) technique, it has recently been reported [22] that CeCoIn5 is characterized by a multitude of gap-values, the greatest among
these being (5.5 ± 0.05) × 10−4 eV. This value has been specifically attributed to the region of ![]() pairing.
pairing.
The investigation reported here too has led to a multitude of ∆0 values―in the (2.76 - 3.49) × 10−4 eV range for pairing via the Ce ions with θD = 73.3 K―corresponding to a single Tc value. The fact that our maximum value is lower than the maximum value reported in [22] is not surprising in view of the mean-field approximation on which it is based.
That there must be an attribute of CeCoIn5 which causes it to have the above features (single Tc, multiple gaps) is obvious. By and large, μ is believed to be that attribute because ∆0 is supposed to follow its fluctuations. The new feature of our approach is the suggestion that HFSCs be addressed by incorporating μ into the BCS equations for Tc and ∆0. Implementation of this suggestion led us to consideration of four equations: the μ-incorpo- rated BCS equation for Tc and the corresponding number equation, besides the μ-incorporated BCS equation for ∆0 and the number equation at T = 0. While the latter two equations have provided the starting point of all papers that have addressed the problem of the BCS-BEC crossover physics, what seems to us to have escaped serious attention is that, upon modification, they can also be used to account for the properties of HFSCs. While indeed modification requires truncation of the equations when μ < kBθD, we recall that such a need also arises for the same reason (i.e., to avoid solutions with complex values) in the study of 1) the crossover physics without appeal to scattering length theory [16] , 2) various Bose condensates via a linearly perturbed harmonic oscillator potential [23] , and 3) the puzzle posed by the dilute SC SrTiO3 [17] . Note however that even though the use of truncated equations for CeCoIn5 here and SrTiO3 earlier is a common feature of our approach, the values of μ and the exact amounts by which the limits of these equations are curtailed are different in the two cases because of the differences in the structures of the SCs. Apart from the rather straightforward mathematical requirement of avoiding solutions with complex values, truncation of the BCS equations can be justified on physical grounds by appealing to itinerancy of electrons. This much-invoked concept was perhaps first used by Suhl et al. [24] in the context of multi-band superconductivity. Since then it has been used routinely for multi-gap superconductors including HFSCs. It was noted in [17] that itinerancy of electrons can cause them to be in a region akin to a “rain-shadow” region where the entire spectrum of phonon energies is not available to them for pairing. We give below an analogy by way of further elaboration.
Imagine a convoy on a road passing through a range of mountains. As the road twists and turns through a series of valleys and mountain-tops, the amount of sunlight the convoy receives will vary from a maximum at the highest point of the range to a minimum at a place determined by its topography. Since 3-d Fermi surfaces of HFSCs are known to have many sheets and highly complex structures, they may be thought of as providing a similar backdrop for the streams of conduction electrons. It then follows that there will be places on the Fermi surface where itinerant conduction electrons can exchange phonons with either the A- or the B-ions separately, besides a place or places where they can exchange phonons with both of them simultaneously; also that the phonon energies available to them for pairing in these places may well be restricted.
Implicit to our approach is the assumption of a locally spherical Fermi surface [LSFS] for each value of μ that we have used. We should like to stress that this is similar to what is done for elemental SCs which too have rather complex structures, as can be seen in [25] . The difference between an element and any composite material is that the latter is characterized by more than one mean value of μ. Hence the approach followed here may be viewed as modeling of a very complex situation in a rather simple (if not the simplest possible) manner. It seems interesting to observe that the concept of LSFSs is reminiscent of the concept of locally inertial coordinate frames employed in the general theory of relativity [26] .
For low values of μ, the difference between these and the corresponding values of ![]() and
and ![]() in the two tables is rather pronounced. This warrants a comment because not only are μ and EF generally used interchangeably in the superconductivity literature, but also because no distinction is made between the values of EF at T = 0 and T = Tc. While both EF and μ signify the amount of energy required to add one particle to the existing many-particle system, strictly speaking, the former is a concept applicable to a non-interacting system whereas the latter applies to an interacting system. Since temperature lifts the degeneracy of a non-interacting system of fermions at T = 0, it follows that
in the two tables is rather pronounced. This warrants a comment because not only are μ and EF generally used interchangeably in the superconductivity literature, but also because no distinction is made between the values of EF at T = 0 and T = Tc. While both EF and μ signify the amount of energy required to add one particle to the existing many-particle system, strictly speaking, the former is a concept applicable to a non-interacting system whereas the latter applies to an interacting system. Since temperature lifts the degeneracy of a non-interacting system of fermions at T = 0, it follows that ![]() should be greater than
should be greater than![]() , as is also seen from the two tables. Further, because interactions cause a reduction in the number of free electrons because of pairing, it follows that μ should be less than both
, as is also seen from the two tables. Further, because interactions cause a reduction in the number of free electrons because of pairing, it follows that μ should be less than both ![]() and
and![]() , as is also reflected in the two tables. While we have so far talked about low values of μ, we note that the inequalities
, as is also reflected in the two tables. While we have so far talked about low values of μ, we note that the inequalities ![]() hold for any value of μ, as can be seen even from the top row in Table 1. We also note that for
hold for any value of μ, as can be seen even from the top row in Table 1. We also note that for![]() , the differences between them show up in the fifth or sixth places after the decimal.
, the differences between them show up in the fifth or sixth places after the decimal.
We now draw attention to the two figures in this paper. The first of these has a dome-like structure, which implies that one can have the same value of λ for two different values of μ. The import of the second figure is that the same value of λ―when combined with different values of μ―leads to different values of ∆0. We note that the parabolic feature of Figure 2 brings out that the variation in ∆0 for decreasing values of μ (for T = Tc) is similar to its variation for increasing values of T (when![]() ).
).
We should finally also like to draw attention here to a study of the de Haas-van Alphen oscillations in the BCS theory that took into account an external magnetic field via the Landau quantization scheme [27] , but not the chemical potential. A further extension of ET that incorporates an external magnetic field may well lead to additional insights about HFSCs.
7. Conclusion
We have shown here that even the so-called exotic or unconventional SCs can be brought into the purview of an extended form of BCS theory which is based significantly on ideas due to Born and Karmann [20] , Suhl et al. [25] , and Bianconi et al. [9] . The application of the modified theory to CeCoIn5 has shed light not only on its Tc(s) and multiple gaps, but also on the mass values of its heavy electrons and their number densities.
Acknowledgements
The author acknowledges that participation in QCM14 at Obergurgl, Austria, stimulated his interest in the superconductivity of HFSCs. He is grateful to the Organizers of this Workshop for their support enabling his participation. He thanks Professor V. S. Varma for a valuable discussion and for verification of some of the numerical work. He also acknowledges that his correspondence with Dr. Eagles and Professor M. de Llano was valuable in this study. He would specially like to thank Mr. Ashwani Kumar, School of Physical Sciences, Jawaharlal Nehru University, for assistance in connection with some of the numerical work. Finally, he thanks Professor D. C. Mattis for encouragement.
NOTES
*Present address: B-208 Sushant Lok I, Gurgaon, Haryana, India-122009.