1. Introduction
The optimal forest harvest models development is marked by the emergence of two controversial issues. The first issue was formulated in its early beginning by Faustmann in 1849 . He formulated a multiple rotation version considering the dynamic effect that the future renovations had in the rotation period of the cut and planting of the trees. The issue was not considered relevant by researchers and forester management, who preferred a simple rotation or Vicksell model. The Faustmann model was finally rediscovered, first by Gaffney in 1957 , and finally by Samuelson in 1976 , who validated Faustmann’s deterministic formula as the correct one, since it was the only one to consider the cost of land rent. An increasing number of researchers continued extending this model (Brazee, 2001; Chang, 2001; Amacher et al., 2011) . The second issue was strongly formulated by Samuelson (1976) , calling to replace the simple notion of stationary equilibrium by the notion of perpetual Brownian motion of wood price. Many researchers followed his recommendation and considered the single rotation problem as an American call option, taking into account wood price as a geometric Brown diffusion (see, Newman, 2002; Clarke & Reed, 1989 ; Thomson, 1992; Platinga et al., 1998). Other authors also considered the wood stock as a second geometric Brown diffusion (Morck & Schwartz, 1989; Insley, 2002) , or as a Logistic diffusion (Alvarez & Koskela, 2007; Navarrete, 2011) . Willassen (1998) introduced uncertainty to the Faustmann model, incorporating the forest growth as a stochastic Markov diffusion process and characterizing the properties of the optimal solutions. Sodal (2002) simplified Willassen’s approach in a closed-form rotation formula for the same state stochastic variable and Insley & Rollins (2005) proposed a numeric algorithm to solve its Hamilton-Jacobi- Bellman solution. Navarrete & Bustos (2013) extended the Faustmann model considering, price as a geometric Brown and wood stock as a Logistical or Gompertz, diffusions processes, transforming the model into an equivalent optimal stopping problem, in spite of its contribution. This paper requires some improvement which will be done in the present paper. Therefore this paper has two basic objectives. In section 2.3, the proof of the equivalence of the Faustmann rotation model under Brown Price and ITO wood stock independent diffusion processes and a one dimensional modified wood stock Optimal Stopping problem is formalized as a reformulation lemma. In section 4, a new algorithm is developed to obtain the Faustmann equivalent one dimensional optimal stopping solution, intersecting the optimal condition curve with the expected wood stock growth feasibility restriction. Finally new stands growth data for the middle age 11 and 12 years is incorporated in Section 3, in order to validate Vicksell and Faustmann stands cut models, under price and wood stock uncertainty.
2. Stochastic Harvest Models
2.1. Stochastic Harvest Stands Rotation Models
The basic model considers two independent stochastic processes: an ITO diffusion for the wood stock, Equation (1) and a geometric Brownian diffusion, Equation (2). The functional objective for the single rotation is given by Equation (3) and for the multiple rotations by Equation (4) see Johnson (2006) :
 (1)
(1)
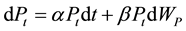 (2)
(2)
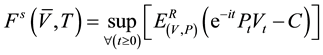 (3)
(3)
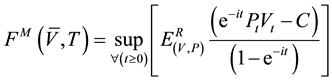 (4)
(4)
Model notation:
Deterministic state variable Economic Parameter
t = Wood stock age C = Stand regeneration cost
Stochastic sate variables P0 = Price at time 0
Vt = Wood stock c = C/P0
Pt = Wood stumpage price at time t R, Q = Probabilistic metrics
Diffusion Parameters F, Z = Functional objective
Wv = Wiener wood stock i = Risky rate of return
μ(V) = Wood stock diffusion drift rate parameter rT = , Capitalized rate of return
, Capitalized rate of return
σ(V) = Wood stock volatility parameter Optimal Parameters
Wp = Wiener price T = Optimal cut time
α = Wood price diffusion drift rate 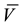 = Expected optimal cut volume
= Expected optimal cut volume
β = Wood price volatility
2.2. Reformulation of the Simple Harvest Rotation Problem
The stochastic model (1) (2) and (3) is difficult to solve due to both diffusions. But it is equivalent to the following one dimensional diffusion Optimal Stopping problem, (5) and (6) see Navarrete (2011) .
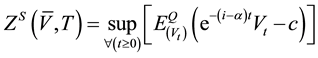 (5)
(5)
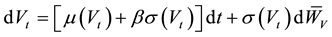 (6)
(6)
The solution of this problem is given by the (HJB) Equation (7), see Navarrete (2011) .
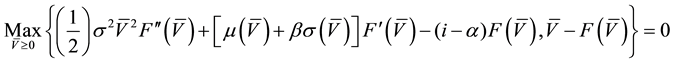 (7)
(7)
Assuming the existence of a frontier V* that divides the zone into a continuation zone (no-cutting) and a stopping zone (immediate-cutting), the solution to the equation HJB is given by (8) for the continuation zone (8) and stopping zone (9). A solution of (8) is given by (10) (see Johnson, 2006 ).
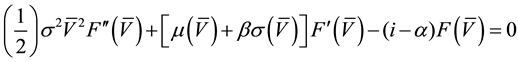 (8)
(8)
 (9)
(9)
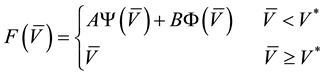 (10)
(10)
where 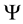 (resp.,
(resp., ) is strictly increasing (resp., decreasing), function since the payoff function are bounded and small, V is positive and should remain bounded and positive a V→0, necessarily then B→0. The solution also fulfils the smooth-pasting condition at the free boundary point V*, equations (11) and eliminating the constant A gives Equation (12).
) is strictly increasing (resp., decreasing), function since the payoff function are bounded and small, V is positive and should remain bounded and positive a V→0, necessarily then B→0. The solution also fulfils the smooth-pasting condition at the free boundary point V*, equations (11) and eliminating the constant A gives Equation (12).
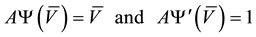 (11)
(11)
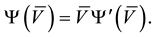 (12).
(12).
2.3. Reformulation of the Multiple Harvest Rotation Problems
The Faustmann optimal rotation model (1) (2) and (4) its equivalent to the following Optimal Stopping one dimensional diffusion problem (13) and (14), see Lemma 1.
Lemma 1. Reformulation Lemma:
The Faustmann optimal rotation problem is equivalent to the following Optimal Stopping one dimensional diffusion problem (13) and (14).
![]() (13)
(13)
![]() (14)
(14)
Proof:
Given the independence of both variables the expectation can be calculated as the product of two independent expectation “![]() ” that are independent of the deterministic parameters
” that are independent of the deterministic parameters ![]() and
and ![]() and the constant C, so they can be taken outside its domain. Introducing the integration of the price Brown diffusion
and the constant C, so they can be taken outside its domain. Introducing the integration of the price Brown diffusion
![]() with
with ![]() and C = P0c in the functional objective (4) results in the objective (15) and reduce the Faustmann problem to the following one dimensional diffusion problem (15) and (16).
and C = P0c in the functional objective (4) results in the objective (15) and reduce the Faustmann problem to the following one dimensional diffusion problem (15) and (16).
![]() (15)
(15)
![]() (16)
(16)
Dividing the objective functional (15) by the constant P0 and applying the Thijssen version of the Girsanov theorem to Equations (15) and (16), for the Martingale Mt and the Radom-Nykodym derivative ![]() (see Thijssen, 2010, Appendix A) permits to reformulate the problem (13) (14) by its equivalent Q metric optimal stopping problem (16) and (17).
(see Thijssen, 2010, Appendix A) permits to reformulate the problem (13) (14) by its equivalent Q metric optimal stopping problem (16) and (17).
The formulation of the HJB equation for this problem is given by Equation (17) for the capitalized risky rate of return ![]() see Navarrete & Bustos (2013) .
see Navarrete & Bustos (2013) .
![]() (17)
(17)
In this case the differential equation for the continuation region ![]() is given by the non homogenous differential Equation (18), and by Equation (19) for the stopping zone
is given by the non homogenous differential Equation (18), and by Equation (19) for the stopping zone![]() .
.
![]() (18)
(18)
![]() (19)
(19)
The solution to the ordinary differential equation, (18) under the initial condition for a given risky rate of return rT is given in Equation (20), with![]() , the positive increasing solution of the homogenous part and
, the positive increasing solution of the homogenous part and ![]() the particular solution of Equation (18).
the particular solution of Equation (18).
![]() (20)
(20)
In this case the smooth pasting condition for each parameter rT are given by Equation (21):
![]() (21)
(21)
So ![]() must fulfill smooth-pasting condition (22) for each parameter rT.
must fulfill smooth-pasting condition (22) for each parameter rT.
![]() (22)
(22)
2.4. Wood Stock Sigmoid Diffusion Equations
The basic requirement of a pine stand growing diffusion is its sigmoid pattern (Garcia, 2005) . The logistic diffusion, Equation (23) is a special case of the sigmoid model given by ![]() and
and![]() , where µ and γ are the drift and saturation parameters and σ is the volatility parameter.
, where µ and γ are the drift and saturation parameters and σ is the volatility parameter.
![]() (23)
(23)
The integration of the value of V is given by Equation (24) (Kloeden & Platen, 1992: p. 125) and its expected value is given by Equation (25)
![]() (24)
(24)
![]() (25)
(25)
Other important sigmoid diffusion is the Gompertz geometrical diffusion, which is given by Equation (26), which is integrated to the expression (27), and its expected values given by expression (28) (see Gutierrez, 2009).
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
The Geometric Brown Price diffusion is given by Equation (29), and integrates in Equation (30).
![]() (29)
(29)
![]() (30)
(30)
3. Experimental Data and Parameter Fitting
3.1. Logistic Diffusion Fitting
The experimental data belonged to 122 harvest pine stands of a Chilean Forest Company in the Araucania Chile region, between years 1999 and 2005 (see Appendix A), and came from different sample plots, with site indexes between 30 and 35 meters, representing sites with high forest aptitude and a tree average initial volume of 32 m3/ha at the first 4 years after initial seed cultivation period. The additional 20 point for years 11 and 12 were taken from Alvarez et al. (2012). The business harvest cut data for a Logistic diffusion for the 95% confidence range is given by data point plotted in Figure 1.
The logistic diffusion parameter cannot be adjusted by maximum verisimilitude, see (Beskos et al., 2006) , so it was fitted using a logistical nonlinear regression and a Monte Carlo/Bootstrap simulation sampling method, implemented by Meyer et al. (Loglet Lab.1 software, 1999) . Choosing V0 = 1/2γ = half saturation volume, and T0 = Tm, time to achieve that volume, Equation (25) is transformed into the more conventional expression (31).
![]()
Figure 1. Wood volume per hectare, (m3/ha) versus years.
![]() (31)
(31)
With; 1/g = saturation volume, m = growth rate parameter, Vs = Saturation volume and tm = time to achieve the midpoint of the saturation volume. The standard deviation Sd(∞), at the saturation zone is constant, and given by Equation (32).
![]() (32)
(32)
Since the saturation volume Vs is also constant, sigma can easily be estimated by Equation (33) and the summary of the parameter fitting is shown in Table 1.
![]() (33)
(33)
3.2. Gompertz Diffusion Fitting
The Gompertz model can be fitted by common statistic features, such as maximum verisimilitude (see Gutierrez et al., 2008 ), but the lack of equal time distribution of data make it difficult. So a quadratic fitting method was development using the SSPS software. By taking natural logarithm and arranging it we get Equation (34).
![]() (34)
(34)
with ![]() (35)
(35)
Given a value for k, a quadratic fitting for ![]() and
and ![]() was done estimating the value of A, B and C until a common value for θ was obtained from A and B, determining the estimation for θ, k and σ. The deterministic parameter only requires a linear fitting with
was done estimating the value of A, B and C until a common value for θ was obtained from A and B, determining the estimation for θ, k and σ. The deterministic parameter only requires a linear fitting with![]() . Both fittings were done for the initial value V0 = 32 (m3/ha) and the results are summarized in Table 2.
. Both fittings were done for the initial value V0 = 32 (m3/ha) and the results are summarized in Table 2.
3.3. Wood Price Diffusion Fitting Equations and Regeneration Costs
The stumpage stand price Brownian diffusion parameters are estimated from saw logs and pulp logs exportation prices (see Appendix B). The summary of Brown diffusion parameters for the stumpage price and the regeneration cost of radiata Pine Stands are given in Table 3, see Navarrete & Bustos (2013) .
4. Stochastic Optimal Pine Harvestings Results
4.1. Logistic Wood Stock and Brown Stumpage Price models
The deterministic optimal solution given by![]() , for the simple rotation model and by equation (36) for the multiple rotation model, see Navarrete (2013).
, for the simple rotation model and by equation (36) for the multiple rotation model, see Navarrete (2013).
![]()
Table 1. Logistic fitting parameters.
![]()
Table 2. Gompertz diffusions parameters estimations.
![]()
Table 3. Radiata pine price diffusion parameters and capital and regeneration stands costs.
Source: Appendix B.
![]() (36)
(36)
The solution of the Vicksell and Faustmann model under Brown price and Logistic wood stock diffusion requires the solution of the differential Equations (8) and (19) for ![]() and
and![]() . The positive increasing function ψ(V) for the Vicksell model, is the solution of the homogenous component (37) of the differential Equation (8) with rT = i in the Vicksell case.
. The positive increasing function ψ(V) for the Vicksell model, is the solution of the homogenous component (37) of the differential Equation (8) with rT = i in the Vicksell case.
The solution of Equation (37) is given by the Kummer’s confluent hyper geometric function, expression (38) with the positive root θ by Equation (39), ψ(V) also must fulfill the smooth pasting condition (12), which was programmed in Mapple 15, see Navarrete (2013).
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
The Faustmann stochastic optimum requires the solution of the differential Equation (16), so the positive function ψ(V) is the solution of its homogenous Equation (37) for the parameter rT and also fulfill the smooth pasting condition, (22). For a given value of the capitalized interest ![]() Equation (37) can be solved using the same methodology of the Vicksell solution, generating a family of optimal cuts for the different parameters rT. The optimum solution is obtained intersecting the optimal parametric solution for different T with the corresponding expected value logistical modify diffusion, (14) for
Equation (37) can be solved using the same methodology of the Vicksell solution, generating a family of optimal cuts for the different parameters rT. The optimum solution is obtained intersecting the optimal parametric solution for different T with the corresponding expected value logistical modify diffusion, (14) for![]() , see Figure 2. The summary of all optimal cuts results for the aggregate 30/35 site index series of the multiple and simple rotation harvest model under Brown price and Logistic wood stock diffusions is given in Table 4.
, see Figure 2. The summary of all optimal cuts results for the aggregate 30/35 site index series of the multiple and simple rotation harvest model under Brown price and Logistic wood stock diffusions is given in Table 4.
The simple optimal cut is a better explanation of the company cut policy, since it only underestimates it in a 2.5%. As expected the Faustmann optimal cut is lower and underestimate the company policy in 11.5%. The deterministic optimal cuts are even worse and underestimate the company policy in 23.4% in the simple model and in 25.6% in the multiple cases. Finally the Logistic wood stock underestimates the saturation Volume in 4.2%.
4.2. Gompertz Wood Stock and Brown Stumpage Price Case
The deterministic optimal solution, is given by ![]() for the simple rotation model and for Equation (41) for the multiple rotation case the optimal is obtained intercepting condition (40) with Equation (27). See Navarrete (2013).
for the simple rotation model and for Equation (41) for the multiple rotation case the optimal is obtained intercepting condition (40) with Equation (27). See Navarrete (2013).
![]() (40)
(40)
![]()
Figure 2. Faustmann logistic optimal cut.
![]()
Table 4. Optimal harvest rotation optimal results, Brown price logistic wood stock diffusion.
The solution of the Vicksell and Faustmann model under Brown price and Gompertz wood stock diffusion requires the solution of the differential Equations, (8) and (16) for ![]() and
and![]() . The stochastic increasing function ψ(V), for these cases is given by the solution of the homogenous Equation (41) with rT = i for the simple rotation case and the capitalized rate of interest rT for the Faustmann case.
. The stochastic increasing function ψ(V), for these cases is given by the solution of the homogenous Equation (41) with rT = i for the simple rotation case and the capitalized rate of interest rT for the Faustmann case.
![]() (41)
(41)
Replacing the parameters given in Equations (42) in (41), gives the differential Equation (43) of the Exponential, Ornstein-Uhlembeck diffusion whose positive increasing solution ψ(V) is given by Equation (44) (see Johnson, 2005), with:![]() , b = 0.5 and
, b = 0.5 and ![]()
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
The optimal solutions also requires that ψ(V) fulfills the smooth pasting condition (38), which is programmed in Mapple 15 generating one optimal cut solution for the Vicksell model and a family of optimal cut condition parametrized by T for the Faustmann case. In this late case the optimal solution is obtain intercepting the family with the expected volume of the Gompertz modify diffusion (20), see Figure 3.
The deterministic and stochastic optimum were programed in Maple 15, using in this case the KummerU function of the program, the results are summarized in Table 5. These results show that the simple stochastic rotation model under Brown Price and Gompertz wood stock diffusion is a better explanation of the company cut policy, since it only overestimates it in 1.2%. As expected, the Faustmann model has lower optimal cut and underestimate it in 9.2% and the deterministic optimal cut is even lower, and underestimate the company policy in 27.9% in the simple case and in 33.1% in the multiple cases. Finally, the Gompertz wood stock overestimated the Saturation volume in 8.6%.
5. Conclusions
1) The optimal cut company policy validates the use of the simple stochastic rotations model under Bown price and Logistic or Gompertz wood stock diffusion.
2) The discrepancy in the theoretical and practical cut policy can be explained by the preference that the business policy gives to shorter rotations periods 25 or less years due to the high organizational risk of the industrial sector in Chile.
3) The Gompertz and Logistic diffusion models present small estimation differences in the growing phase of wood stock, but significant differences in the saturation volume of the wood stock, which should be crucial in the model diffusion selection.
Acknowledgements
The author acknowledge the collaboration of P. Santibañez of MININCO (2006) forest company for providing with the Radiata pine stands harvest near Temuco and to “Modelo Nacional de Simulación de Pino Radiata” for the complementary stands data of the region.
![]()
Figure 3. Faustmann gompertz optimal cut.
![]()
Table 5. Optimal harvest rotation optimal results, Brown price Gompertz wood stock diffusion.
Appendix A: Mininco Radiata Pine Stands Harvest Data
Notes: TVOL = Total Volume (mts3/ha); TVOL = POD + DEBO + INDUST + COMERC + PULPA POD + DEBO = Wood thinning cuts; Logs composition: Saw logs = INDUST + COMERC = 83.9%; Pulp logs = PULP + POD + DEBO = 16.1%; Saturation volume Vs = 601.6 m3/ha, (3% stands biggest TVOL average).
Appendix B: Radiata Pine Log Prices
![]()
Table B1. Nominal Radiata Pine log exportation prices.
Source CONAF-INFOR Chile.
The Price diffusion parameters can very easily be calculated by making the following logarithmic transformation![]() . The parameters are given by Table B2.
. The parameters are given by Table B2.
![]()