Model of Hydrogen Deficient Nebulae in H II Regions at High Temperature ()
1. Introduction
At a basic level, planetary nebulae can be thought as quite of gas consisting typically of about 90% hydrogen, about 10% of helium, and trace amounts of heavier elements such as carbon, nitrogen, oxygen, and so on, which in most cases is more or less regular in shape.
Depending on the size and density of the nebula, it may be either matter bounded or ionization bounded. In the former case, there are enough ionization photons to ionize all the neutral hydrogen in the nebula while in the latter case; UV radiation cannot penetrate beyond an ionization front outside which hydrogen will remain neutral.
The gas in these nebulae cloud is mainly hydrogen. The next most abundant element is helium whose relative abundance is the order of 10%. This element can exist in neutral form in H II region [1] . The proportions of the other elements, which are less abundant than the main elements, have a proportion of 1%. In general, hydrogen which is dominant and presents in the form of molecules and atoms [2] . These clouds are called H I regions i.e. clouds of neutral hydrogen. When these clouds are heated by the stars with the radiation 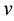 >
> 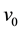 [3] , where
[3] , where  is the hydrogen ground state ionization limit, will be referred to as ionizing radiation [2] . The gas temperature increases as radiation intensity increased and the hydrogen is totally ionized. Because of this radiation hydrogen is found in the region which is called H II regions.
is the hydrogen ground state ionization limit, will be referred to as ionizing radiation [2] . The gas temperature increases as radiation intensity increased and the hydrogen is totally ionized. Because of this radiation hydrogen is found in the region which is called H II regions.
Stars are formed in molecular clouds of star forming regions. Molecular clouds consist mostly of hydrogen but they also contain molecules and dust. At some moment, parts of these dense clouds start to collapse. Gravity does the rest [2] . As more material is accumulated the force of the gravity increases and therefore more material is attracted. This cumulative process involves an increase in temperature in the inner regions. The temperature rises until at some moment it is able to ignite nuclear reactions and it is then that we can say that a star is born. Regardless of the mass, stars spend most of their life burning hydrogen in the core to produce helium.
As the star evolves, further thermonuclear reactions take place in the interior of stars. Via these reactions, stars produce helium and metals. These are brought to the surface in a series of dredge-up events that take place at different stages in stellar evolution. In the latest stages of evolution the star experiences mass loss episodes. By the ejection of the outer layers the planetary nebula returns gas to the interstellar medium that has been enriched with metals from which new generations of stars will be formed. In this way, by the ejection of the outer layers planetary nebulae (PNe) contribute to the enrichment of the ISM [2] .
The present work covers the same topic as the work of [4] who calculated the ionization structure of hydrogen, helium, oxygen and the profiles of temperature and electron number density. In particular he developed model of hydrogen deficient nebula by dropping hydrogen density by 10. In this work we develop a new model of hydrogen deficient nebular for non-uniform hydrogen density with and without grains.
2. Basic Physics of Gaseous Nebulae
The understanding of the physics of ionized gases is crucial to many subjects in astronomy. Emission spectra can be observed from numerous astronomical objects and the interpretation of these spectra is essential to understand, and scientifically describe them. The study of lines in these spectra has yielded valuable information regarding the most elementary atomic processes occurring in the Universe and has proven to be an essential tool in astronomy [5] .
Gaseous nebulae are often permeated by an external radiation field, generally from a nearby star or stars. The particles (atoms, ions and electrons) in the nebula and the photons of the radiation field interact in such way that the physical properties of the nebula can be deduced by studying the resultant light coming from the plasma. To model the theoretical spectrum that we would expect to see from a specific nebula, it is necessary to have a detailed knowledge of the microscopic processes occurring within the nebula.
The temperature of electron plays a vital role in the formation of nebulae. It is defined from the motion of free electron gas, which has a velocity distribution described be Maxwell distribution [3] . It is set by the balance of energy between input energy is set to the processes and loss of energy through it [8] . This energy is produced by the process of photoionization of ions or atoms and recombination of ions with atoms.
Photoionization is a common process in the interstellar medium (ISM) and in circum-stellar material [4] . It happens when gas is being irradiated and ionized by photons from an external source. The ionizing source is usually a star or an ensemble of stars, but could also be an accretion disk. Typically the distance of the ionizing source is much larger than the diameter of the source, implying that its radiation field is strongly spherically diluted when it reaches the gas.
Photoionization is analogous to the bound-bound process of absorption. This process involve a bound electron of an atom being liberated to the continuum due to the absorption of a photon, [6]
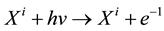 (1)
(1)
where  is an atom,
is an atom,  is the energy which is used for ionizing atom,
is the energy which is used for ionizing atom, 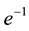 is electron released through the process and
is electron released through the process and 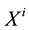 is the ionized atom. The ionizing photon has to have a higher energy, and thus higher frequency, than one involved in a bound-bound absorption reaction from the same level, as the incoming photon has to have sufficient energy to lift the electron to a free state from the outer shell.
is the ionized atom. The ionizing photon has to have a higher energy, and thus higher frequency, than one involved in a bound-bound absorption reaction from the same level, as the incoming photon has to have sufficient energy to lift the electron to a free state from the outer shell.
The photoionized gas can be characterized by an electron temperature and the abundances of each ionization stage of every element (the ionization structure). The ionization structure implies an electron density (charge conservation). Each ion is characterized by the level populations of each of its electronic states [7] .
It is commonly assumed that the electrons have a perfect Maxwellian distribution [3] . Deviations do exist near strong temperature gradients (solar corona) and from secondary electrons due to cosmic ray ionizations (molecular regions). The dominant processes determining the ionization structure are photoionization and its inverse process, radiative recombination [8] .
Cloudy is a photoionization code commonly used by astronomers [9] . It calculates the synthetic spectrum of the ionized nebulae given the parameters of the star and of the diffuse gas as well as its thermal, ionization and chemical structure. The luminosity and the shape of the ionizing continuum, as well as the particle density and the chemical composition of the gas must be defined. One can use blackbody shape as the ionizing continuum or define a certain in shape based on the stellar population synthesis predictions. Additionally, the geometry of the gas must be defined. It is a spherically closed geometry and corresponds to optically thin nebulae [1] [10] .
3. Models
In this section, we compute photoionization models for hydrogen deficient nebulae. In order to explain the ionization structure of elements, we consider a gas is ionized by a blackbody of temperatures 150,000 K with a radius of the star is log(r) = 10.
A photoionization model must be used to discover the physical structure of the nebulae. Models are not a direct and exact depiction of reality, but can help to extend or reconstruct our understanding of it [11] . The quality of data fed into the model, as well as a competent acquaintance with the assumptions that are equally important to improve our knowledge of a particular physics object or situation.
The simplest and most frequently used model in hydrogen deficient nebula is dedicated to determine ionization structure of H, He, O, temperature and density of electron profiles [4] . To do so, we develop both uniform and non-uniform hydrogen density models. But we assumed that in both cases abundances of heavy elements described in Table 1 given by [4] remain the same and peak value of hydrogen density varies from 104 to 10 cm−3. In the first hand we want to test uniform density distribution that was done by [4] , in the second hand, we will use to test non uniform hydrogen density described by Equation (2) with and without grains. We use the photoionization code CLOUDY version C13.1 given in [9] to calculate the models of hydrogen deficient nebulae exposed to the blackbody radiation. We assume ionization bounded spherically symmetric, which means that the ionization photon escape fraction is zero. The output of the CLOUDY model give detail measurements of temperature of electron, electron density, ionization structure of hydrogen, helium and oxygen [12] .
The Theoretical Models
A full description of the theoretical photoionization models given in [4] suffice it to say that the basic model consists of steady state. We want to compare the previous model with non-uniform density distribution which varies exponentially with the distance. Spherical symmetric dust free nebulae of uniform density of hydrogen plus ions have been considered to solve this problem [4] . This work is assumed hydrogen density is non-uniform and given by the power law radial density shown in Equation (2)
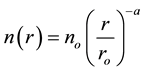 (2)
(2)
where no is the number density at the illuminated face of the cloud, will be 104 cm−3,  , which means the
, which means the
![]()
Table 1. Elemental abundances used in the nebular mode [4] .
density will be proportional to the inverse square of radius and n(r) is the total hydrogen density at a distance r from the source, and 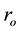 is the radius of the inner sphere.
is the radius of the inner sphere.
The abundances of ions are shown in Table 1. The central ionizing star has a blackbody temperature 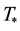 = 150,000 K and a radius
= 150,000 K and a radius 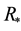 = 1010 cm and the nebula has inner radius of
= 1010 cm and the nebula has inner radius of 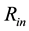 = 1017 cm and was terminated when the temperature falls below 100 K. The filling factor is assumed to be one.
= 1017 cm and was terminated when the temperature falls below 100 K. The filling factor is assumed to be one.
The elements considered for the nebular heating (by photoionization), cooling and opacity are H, He, N, C, O, and Ne. Those will be referred to as primary elements. These determined the electron temperature, ionization structure of some of elements. A nebula parameter is the chemical composition of the gas, given in Table 1.
The most important of these abundances is that of O, which the principal is almost always coolant in planetary nebulae (PN) is among the most important cooling agents in PNs and as such, play a major role in determining the thermal and ionization structure of the nebulae and relative intensity of all emission lines.
This model was first tested by [3] and again by [4] . This is radiation nebulae model, which is similar to H II regions. It has its own constraint, but what happen to this model when the abundances of all heavy metals are constant but the total hydrogen density is non-uniform which depends on distance from the radius.
4. Results and Discussion
The essence of this work is to explore the behavior of the ionization structure of hydrogen, helium, electron temperature and density in carbon dominant nebulae. It is important to note that the ionization parameters depend on hydrogen deficient nebulae.
4.1. The Standard Model
Figure 1 shows the ionization structure of H, He through shell, as well as Ne, and Te profiles. The temperature and electron number density are normalized relative to peak value of 1.665 × 104 K and 1.202 × 104 cm−3 respectively. The size of Stromgren sphere n( H II) = n(H I), which occurs at about 1.5 × 10 17 cm. Both hydrogen and Helium ions are ionized by the hot central star and helium stars to dominate from the radius of 1.4 × 10 17 onwards. These were already tested by [4] . In the inner edge of the nebulae both H+ and He2+ ions are dominant since the ionization energy to ionize both elements is greater than 4.8 Ryd or 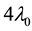 .
.
In the model shown in Table 1, oxygen is the less abundant than carbon, and it has a more impact to cool down the gas efficiently rather than carbon ions. Its ionization structure is shown in Figure 2. It is ionized up to O VII but their abundances are very low relative to the other oxygen ions. In the inner edge of nebulae between from the beginning to 1.1 × 1017 cm, temperature of electrons drops because O III grows in this interval to cool down the temperature of electrons.
![]()
Figure 1. The ionization structure of H and He of the standard model. The dotted lines are normalized temperature Te, and electron density Ne, profiles through the nebula.
![]()
Figure 2. The ionization structure of O of the standard model when the number of hydrogen density is 104 cm−3 with normalized temperature profile.
The model was tested by [4] for hydrogen number density NH = 103, 102 and 10 cm−3. In order to compare the result we obtained for NH = 104 with 10 cm−3, we present only the ionization structure and temperature profiles for hydrogen density of 10 cm−3. Figure 3 shows that the peak temperature of electron changes by 53% when the hydrogen density drops from 104 to 10 cm−3. The rate of falling of temperature is fast and falls down slowly. This is due to rise of the ionization O III to cool down temperature of electron.
4.2. Hydrogen Deficient Nebulae for Non-Uniform Hydrogen Density
We further discuss the possible mechanism of ionization structure of elements and temperature and electron density profiles, especially the requirement to have hydrogen deficient nebulae for non-uniform hydrogen density. We start from the basic assumption that was given in [4] . To test the impacts of non-uniform hydrogen density which vary with α = −0.5 on the ionization structure and temperature profiles of the nebular on the basis of absolute abundances of He, C, O, N and Ne are kept constant. The result shows that hydrogen density decrease in every step by 10 with and with grains.
The normalized temperature profile of electron shown in Figure 4 has similar nature with the Figure 1 shown above. There are some basic differences between these models. In the first uniform model, the peak value of temperature and is increased by 0.016% relative to standard model done by [4] . This is due to the cooling rate of the nebulae mostly by oxygen ions, which is much faster than the standard model and the electron number density, decrease by a factor of 0.7%. In the presence of grains, the normalized temperature, electron density, ionization structure of both hydrogen and helium are shown in Figure 5. The peak temperature of electron is smaller than the previous two models. In all cases, fluctuations of temperatures are so high when grains are included in the models.
Normalized temperature profile of temperature shown in Figure 6. It has peak temperature of 1.8778 × 104 K, which is greater than the standard model. The profile shows, temperature falls down slightly from 1.2674 × 1015 cm from the center of the star and rises up slowly from 1.2 × 1018 cm and drops sharply to 100 K in the last zone. Whereas the ionization structure of hydrogen have the same nature but it differs only the distance at which it extends.
The temperature, density and structure of H in a nebula with hydrogen density N(H) = 103 cm−3 with α = −0.5 is shown in Figure 7. The peak temperature Te = 2.1439 × 104 K, and electron density, Ne = 1.183 × 103 and lower than the standard model. The size of the nebula increased to r ~ 3.7 × 1018 cm, terminating at the end of the H II Stromgren sphere where there is a rapid drop in both Te and Ne. Here we have three zones with the nebulae where the temperature drops at faster rate near the source and falls slowly whereas the rate of drops of electron number density is fast from the center of the source. The ionization structure of hydrogen is dominant throughout the H II regions.
![]()
Figure 3. The ionization structure of H and He of the standard model. The dotted lines are normalized temperature Te, and electron density Ne, profiles through the nebula.
![]()
Figure 4. The ionization structure of O of the standard model when the number of hydrogen density is 10 cm−3 with normalized temperature profile.
![]()
Figure 5. The solid blue and blue dash line are the normalized temperature Te, and electron density Ne respectively, profiles through the nebula when the hydrogen density 104 cm−3, which vary with the power law α = −0.5 with ionization structure of hydrogen and helium with grains.
![]()
Figure 6. The black and magenta dotted lines are the normalized temperature Te profile, through the nebula when the hydrogen number density 104 cm−3, which vary with the power law α = −0.5 and the other lines shows the structure of both hydrogen and helium ions.
![]()
Figure 7. The red and magenta dotted lines are the normalized temperature Te, and electron density Ne respectively, profiles through the nebula when the hydrogen density 103 cm−3, which vary with the power law α = −0.5 with ionization structure of hydrogen.
The ionization structure of oxygen is shown in Figure 8. Near to the ionization front O VII is dominant until it arrives to the distance of 5 × 1017 cm. O IV starts to dominate the ionization processes because of the recombination of ions between O VII and O VI. From 1.75 × 1018 cm, both O III and O II starts to dominate and to cool down the temperature of the nebulae. In the hydrogen deficient nebulae when hydrogen number density falls to n = 102 cm−3 with α = −0.5, carbon abundance is dominant than oxygen. The ionization structure of O through the nebula is illustrated in Figure 9. It is ionized up to O VII but its abundances is greater than O VI from 2 × 1015 to 1.4736 × 1016 cm. and O VI, which starts to increase slightly to reaches peak value 0.541 at 1.0663 × 1017 cm. The O IV is dominant between 2.72135 × 1017 to 1.61791 × 1018 cm and has a peak value of
![]()
Figure 8. The ionization structure of oxygen when the number of hydrogen density 103 cm−3, which vary with the power law α = −0.5.
![]()
Figure 9. The ionization structure of oxygen when the number of hydrogen density 102 cm−3, which vary with the power law α = −0.5.
fractional abundances of 0.623 at a distance 7.15393 × 1017 cm. O III grows from the edge of nebulae becoming the main ion from 6.9741 × 1018 to 1.54055 × 1019 cm. The nebulae lines [O III] λ 5007, λ 4959 produce most of the cooling process in the inner region of nebulae. The temperature profiles shows a rapid increase with the distance from the center before O III starts to dominate in the inner edge of nebulae the number density 100 cm−3 which vary with power law α = −0.5 is depicted in Figure 10. It shows that the peak temperature of electron is 32,155 K. and electron number density as 1.184 × 102 cm−3. The temperature profiles have been increased by 30% whereas the electron number density decreased by 10%. The profiles of both electron number density and temperature have the same nature but they differ in their magnitudes and distance at which drops to zero.
5. Conclusion
The main purpose of this paper had two fold. First, a sequence of hydrogen deficient model has been constructed
which differs in several respects from that of the previous work, both with respect to the defining parameters
![]()
Figure 10. The normalized profiles of temperature and electron number density of hydrogen nebulae 102 cm−3, which vary with the power law α = −0.5.
(radius of star, and density). Second, in the previous investigation hydrogen density was uniform and its peak dropped by the power of 10, in this work, we assumed non uniform hydrogen density deplete by α = −0.5 but the abundances of heavy metals were the same throughout the processes and the radiation field. The elements considered for the nebular heating (by photoionization), cooling and opacity are H, He, N, C, O, and Ne. These determined the electron temperature, ionization structure of some of elements based on the nebula parameter chemical composition of the gas, given in Table 1 for both uniform and non-uniform distribution of hydrogen density. The result shows that if the electron density Ne increased, the temperature of the nebulae will increase since the excited levels of the trace elements become depopulated by collisional de-excitation and not by radiative transitions which serve to cool the nebula.