Gravitational Forces Explained as the Result of Anisotropic Energy Exchange between Baryonic Matter and Quantum Vacuum ()
1. Preliminaries
For convenience, let us recall some basic definitions and notations used in this paper. We apply the SI system of units. The macroscopic Newtonian law defining the force of attraction of two bodies of mass M1 and M2 is
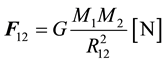 (1)
(1)
where
 (2)
(2)
is the gravitational constant, M1 and M2 are masses of the bodies [kg] and R12 the distance between their center of mass. Using analogies between gravity and electromagnetism it is convenient to apply the reciprocal constant
 . (3)
. (3)
The gravitational field generated by a hypothetical point mass M1 is
 (4)
(4)
is called gravitational acceleration. R is the distance from the center of mass of M1,  a unit vector indicating the direction of the field and rM is the equivalent surface mass density. The minus sign indicates that acceleration is directed towards the center of mass.
a unit vector indicating the direction of the field and rM is the equivalent surface mass density. The minus sign indicates that acceleration is directed towards the center of mass.
Let us remind that:
1) The gravitational field is a vector quantity.
2) Two opposite gravitational fields of the same modulus cancel. Remark: This cancellation should not be interpreted as annihilation The hypothetical gravitons propagating in opposite directions do not collide (see Figure 9 in Appendix B).
3) Ordinary matter (baryonic matter) is transparent for gravitational fields. Differently to electrostatic fields gravitational screens are unknown.
4) The energy density of the gravitational field is given by the equation
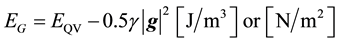 , (5)
, (5)
where EQV is the extremely high energy density of the Quantum Vacuum (QV) (see Appendix C). Note that gravity lowers the energy density of QV differently to the energy of electrostatic field and that energy densities and pressure have the same dimensions.
2. Anisotropy of Energy Distribution around a Mass Induced by an External g-Field
Consider a spherical body with the g-field defined by (B3) in the Appendix B. The self g-field is isotropic, i.e., the magnitude is equal for all directions. In the presence of an external g-field 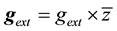 and writing the isotropic surface g-field in the form
and writing the isotropic surface g-field in the form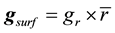 , the resulting surface g-field is given by the formula
, the resulting surface g-field is given by the formula
 . (6)
. (6)
The modulus of this vector is
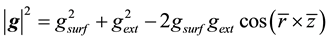 . (7)
. (7)
Evidently, the energy density at the surface of the sphere is anisotropic. For example, if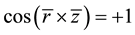 , we have
, we have
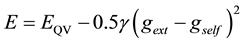 (8)
(8)
and if ,
,
 . (9)
. (9)
This anisotropy is responsible for the existence of a recoil force described in next chapter (See Figure 1).
![]()
Figure 1. Cross-section of the spherical body (yellow). The self g-field (solid arrows) is spherically symmetric. The g-field of a far body (dotted line) penetrates the body with no change of sign. Therefore at the night side we have summation and at the day side subtraction of the fields. The gravitational energy density is lower at the night side w.r.t. the day side.
3. The Schwartzschild Radius and the Highest Value of a g-Field in Nature
The Schwartzschild radius Rsch is defined as the radius of a sphere such that, if all of the mass of a body is compressed within that sphere, the escape speed from the surface of the sphere would equal the speed of light. In this paper we try to apply this notion to calculate the maximum value of the modulus of any g-field. Schwartzschild, using equations of general relativity derived the following form
 . (10)
. (10)
For a sphere of radius Rsch the equivalent surface mass density![]() .
.
Therefore, the surface g-field is
![]() . (11)
. (11)
The gravitational part of the energy density at the surface (see (5) and (11)) is
![]() . (12)
. (12)
For comparison let us calculate the Einstein’s energy density
![]() . (13)
. (13)
Note that the ratio (13)/(12) equals 12. Let us quote the neutron star PSRJ614-2230 with a radius 19,300 [m] and a mass M = 3. 978 × 1030 [kg] (two solar masses). The surface g-field of this star equals 7.13 × 1011 [m/s2]. Its Schwartzschild radius 5911 [m] is only 3.27 times smaller w.r.t. the physical value 19300 [m]. A neutron star with the diameter 5911 [m] and the mass equal to twice the mass of the Sun would have a g-field at the surface given by (11):
![]() (14)
(14)
In this paper we apply this value as the largest possible value of any g-field. Note that the highest value of the g-field is defined macroscopically at the surface of a neutron star. Differently, the highest value of electrostatic field is defined microscopically at the surface of the electron (see [1] ).
4. Derivation of the Formula for Calculation of the Power of the Energy Exchange between a Mass M and the Quantum Vacuum
We formulate a hypothesis that baryonic matter continuously exchange energy with the Quantum Vacuum with zero balance. Let us calculate the power of the emission. In absence of external fields we postulate an isotropic absorption and emission pattern as illustrated in Figure 2. There is no recoil force of radiation. The external g-field induces anisotropy of radiation resulting in a recoil force. Our goal is the calculation of the power of the energy exchange. Our choice is the model of the radiation pattern defined by an ellipsoid
![]() , (15)
, (15)
where e is the eccentricity of the ellipse. This formula uses the polar coordinates centered in the focus of the ellipsoid. The recoil force is given by the integral
![]() , (16)
, (16)
where v is the velocity of radiation, c the velocity of light in free space and ![]() a unit vector directed along the longer axis of the ellipse. The derivation of Appendix A yields for a small value of ε the following formula (v = c)
a unit vector directed along the longer axis of the ellipse. The derivation of Appendix A yields for a small value of ε the following formula (v = c)
![]() . (17)
. (17)
This recoil force should be equal to the gravitation force
![]() . (18)
. (18)
Equating the above formulae yields the following expression for the power P
![]() . (19)
. (19)
Evidently, the calculation of the value of the power P requires the knowledge of the value of the eccentricity e. Following the procedure of defining the eccentricity for electrostatic fields [2] let us define
![]() (20)
(20)
where ![]() is defined by (14). We get the following simple formula
is defined by (14). We get the following simple formula
![]() (21)
(21)
For the model of two parallel planes covered with a mass density rM/2 [kg/m2]t (21) takes the form
![]() (22)
(22)
having the dimensions of the Pointing vector of electromagnetic theory. The Table 1 presents the value of P for selected bodies.
![]()
Figure 2. Left. The cross-section of a circular radiation pattern. Right. The cross-section of an elliptical radiation pattern. In examples the eccentricity is extremely small.
![]()
Table 1. A list of the values calculated using (21).
5. Illustration of the Idea of the Recoil Nature of Gravitational Forces by a Model of a Binary Star
The Nobel prize in physics in the year 1993 has been awarded to R.A. Hulse and J.H. Taylor for the discovery of a binary neutron PSR B1923+16 and precise measurements of the elongation of the orbital period giving the evidence of radiation gravitational waves [3] - [6] . In this chapter we indicate that possibly gravitational radiation carries negative energy. In the binary PSR B1923+16 the two neutron stars of nearly equal masses are orbiting each along a separate elliptical orbit around a common center of mass (Figure 3) The laureates measured the rate of decrease of the orbital period equal 76.5 [ms/year] and calculated the power of the emission of gravitational waves![]() . Our goal can be achieved presenting calculations for a simplified system of two neutron stars with equal masses and a common circular orbit (Figure 4).
. Our goal can be achieved presenting calculations for a simplified system of two neutron stars with equal masses and a common circular orbit (Figure 4).
6. Kinetic Energy of the Neutron Stars on a Circular Orbit
We investigate a model of a binary neutron star of equal masses M1 = M2 = M orbiting on the initial orbit of radius R. The presented theory is well known. We present a convenient version. Equating the gravitational force with the centripetal force
![]() (23)
(23)
yields the following radius of the circular orbit
![]() , (24)
, (24)
where G is the gravitational constant, ![]() is the initial angular velocity and T the initial orbital period. Note that if we assume a loss of energy due to the emission of gravitational waves, w and T are functions of time. However, during one orbital period the change is negligible. The orbital (tangential) velocity is
is the initial angular velocity and T the initial orbital period. Note that if we assume a loss of energy due to the emission of gravitational waves, w and T are functions of time. However, during one orbital period the change is negligible. The orbital (tangential) velocity is![]() .
.
The initial kinetic energy of both stars is
![]() . (25)
. (25)
The insertion yields
![]() . (26)
. (26)
Note that multiplication of both sides of (23) by R yields the equality of the kinetic and potential energies The
potential energy is ![]() and the kinetic energy is
and the kinetic energy is![]() , i.e.,
, i.e.,![]() . Both energies
. Both energies
![]()
Figure 3. Two elliptical orbits of binary neutron stars with a common center of mass. Adapted from [5] .
![]()
Figure 4. A circular orbit of two neutron stars.
differ only by sign. The observations of PSR B1923+16 have shown a decrease of the orbital periods by ![]() per year [3] . Assuming that a similar decrease occurs also in our circular model we get an increase of the kinetic energy
per year [3] . Assuming that a similar decrease occurs also in our circular model we get an increase of the kinetic energy
![]() . (27)
. (27)
The increase of the kinetic energy per year is
![]() , (28)
, (28)
where P is the radiated power and ![]() is the duration of a year in seconds.
is the duration of a year in seconds.
Remark: The kinetic energy and T are functions of time. However, we have no need to apply differential equations since the initial value of ![]() is very small. Note that for a given
is very small. Note that for a given ![]() this equation uniquely defines the value of the power of the emitted gravitational waves. We observe that the emission of gravitational energy causes the increase of the kinetic energy. In consequence, if we assume that the lost of the kinetic energy is caused by the emission of gravitational waves the emitted energy should be classified as negative. This should be understood as periodic lowering of the positive energy of the Quantum Vacuum propagating with the speed of light. In the case of the system reported by Taylor and Hulse the kinetic orbital energy is a periodic function of time. Therefore, (27) and (28) should be replaced by the mean values.
this equation uniquely defines the value of the power of the emitted gravitational waves. We observe that the emission of gravitational energy causes the increase of the kinetic energy. In consequence, if we assume that the lost of the kinetic energy is caused by the emission of gravitational waves the emitted energy should be classified as negative. This should be understood as periodic lowering of the positive energy of the Quantum Vacuum propagating with the speed of light. In the case of the system reported by Taylor and Hulse the kinetic orbital energy is a periodic function of time. Therefore, (27) and (28) should be replaced by the mean values.
7. Selected Data for the Model of a Binary Star with a Circular Orbit
The following data have been selected from data of the PSR B1913+16. The measured initial orbital period T = 27906.97959 [s] and the calculated masses are M1 = 2.8764 × 1030 [kg], M2 = 2.72050 × 1030 [kg]. We applied for our model with the circular orbit the following data:
Equal masses (mean value)
![]() (29)
(29)
The radius of each star
![]() (30)
(30)
The initial angular velocity
![]() (31)
(31)
The initial radius of the circular orbit
![]() (32)
(32)
The initial tangential orbital velocity is
![]() (33)
(33)
The volume mass density of each star is
![]() (34)
(34)
corresponding to the equivalent surface mass density
![]() (35)
(35)
The intensity of the self gravitational field at the surface is
![]() (36)
(36)
The intensity of the g-field at the center of a single star induced by its companion
![]() (37)
(37)
(about twice of the Earth field). The Schwartzschild radius is
![]() (38)
(38)
yielding the value
![]() (39)
(39)
The difference in comparison to (14) is small. The Einstein’s energy density of a single star is
![]() (40)
(40)
The energy density at the surface of the star defined by the power ![]() is
is
![]() (41)
(41)
The energy density of the surface self g-field is
![]() (42)
(42)
8. Arguments in Favor of the Presented Hypothesis about the Physical Origin of Gravitation
1) The existence of the Quantum Vacuum as a medium with extremely high energy density is confirmed by many experiments and is not questioned. Let us mention the experimental confirmation of the predicted Casimir force.
2) Recently researchers have created electrons from “nothing” This nothing is the energy of QV.
3) Recently the scientists from Berkeley University [7] have measured the difference of the Compton frequencies for two groups of cesium atoms, a local group and a second group after a small journey. They confirmed experimentally the Einstein’s twilling effect (time dilation). Certainly, this gives the evidence, that cesium atoms emit energy at Compton frequencies.
4) The gravitation attraction force is not the result of the pressure of the gravitation field on the baryonic matter. For example, in the model of two parallel planes covered with a uniform mass density (see Figure 9 in the Appendix B) the pressure inside the plates is higher in comparison to the outside Since the two plates attract this cannot be the result of radiation pressure of the gravitational field.
9. Conclusions
Many experiments and phenomena confirm that the Quantum Vacuum is a medium with extremely high energy density. Let us mention the Casimir effect and the Lamb shift. A good confirmation gives the electron on the Bohr orbit. Due to the rules of electromagnetism it radiates energy. Without absorption of the energy from the QV it should decay in a short time. This makes the hypothesis that particles absorb and reemit energy from the QV highly probable. Using this hypothesis we derived a formula enabling the calculation of the power of the energy exchange. The value of this power is formidable. However, let us recall the formidable energy density of the QV. Our numerical results depend on the maximum possible value of the intensity of any gravitational field. The eventual application of another value of this constant will change only numerical results. Let us recall that the g-field lowers the energy density of the QV. Our results are valid for the Newton’s law of gravity. In frame of this law, the QV is a linear medium. However, we know that for high density g-fields nonlinear effects occur. For example, the speed of light in vacuum is lowered by gravitation. Gravitational deflection of light beams is well known. Assuming the validity of the statement that gravitational waves carry negative energy, any device constructed to detect gravitational waves should be able to measure periodic variations of the energy density of the Quantum Vacuum, for example, looking for periodic variations of the speed of light. Note the extremely small values of the eccentricity of the radiation pattern. In the worst case of the binary neutron stars, the eccentricity is![]() . The small g-field of the companion star controls the emission diagram of the large power defined by (21). We have a kind of amplification.
. The small g-field of the companion star controls the emission diagram of the large power defined by (21). We have a kind of amplification.
This paper differs from the reference [8] . We presented the derivation of the formula for the power emitted by the mass M (see (21)) and have shown that possibly the gravitational waves carry negative energy in the sense of (5). The examples with neutron stars are new.
Appendix A. Derivation of the Recoil Force for an Ellipsoidal Power Radiation Pattern
We assume, that the angular power radiation pattern (power density per unit solid angle) is given by the rotation around the longer axis of the ellipse
![]() , (A1)
, (A1)
where e is the eccentricity of the ellipse. This formula uses the polar coordinates centered at the focus of the ellipsoid. The recoil force is given by the integral
![]() , (A2)
, (A2)
where v is the velocity of radiation and ![]() a unit vector directed along the longer axis of the ellipse.
a unit vector directed along the longer axis of the ellipse.
The insertion of (A1) and using the projection of the radius centered in the focus on the longer axis (![]() ) yields
) yields
![]() . (A3)
. (A3)
We get inserting v = c.
![]() . (A4)
. (A4)
The evaluation of the integral yields
![]() , (A5)
, (A5)
where
![]() . (A6)
. (A6)
However, smax should be normalized to keep the total power P independent on e. The power gain of the ellipsoid is given by the formula
![]() , (A7)
, (A7)
where B is the equivalent solid angle
![]() , (A8)
, (A8)
where
![]() . (A9)
. (A9)
Since ![]() we get
we get
![]() . (A10)
. (A10)
The insertion of (A10) in (A5) yields
![]() . (A11)
. (A11)
If![]() , the ratio
, the ratio![]() .
.
Appendix B. Selected Simple Models of Gravitational Bodies
Our discussions about the nature of gravitation apply the following simple idealized models of mass bodies.
A sphere of radius R0 filled with a uniform volume mass density (Figure 5)
![]() . (B1)
. (B1)
The above sphere can be replaced by a hollow sphere with an equivalent surface mass density rm [kg/m2]. (Figure 6)
![]() . (B2)
. (B2)
The surface and outside g-fields of both spheres are the same. For the first the g-field is
![]() (B3)
(B3)
and for the second the inside g-field equals zero (Figure 7).
An infinite plane covered with a surface mass density.
![]()
Figure 5. Cross-section of a sphere with a uniform mass density rv [kg/m3].
![]()
Figure 6. The sphere of Figure 5 can be replaced by a hollow sphere with a uniform surface mass density rM. The external fields are the same.
![]()
Figure 7. The visualization of the g-field given by (B3).
Consider the rectangular Cartesian coordinates (x,y,z) and the plane z = 0. We assume that the plane is covered with a surface mass density rM [kg/m2]. This unphysical body could be interpreted as a limiting case of a disc of radius Rd situated between the planes z = −Ñz and z = Ñz assuming Rd ® µ and Ñz ® 0. The g-field of this plane is (Figure 8)
The g-field is
![]() (B4)
(B4)
Two parallel planes located at z = −z0 and z = z0 (Figure 9, Figure 10).
The g-field is
![]() (B5)
(B5)
A single body of any shape or an ensemble of many bodies with a center of mass at the origin The asymptotic g-field at large distance from these bodies decay proportionally to 1/r2 independent of the direction.
Evidence that the gravitational field lowers the energy density of the QV
The evidence is presented in Figure 10.
Appendix C. The Energy Density of the Quantum Vacuum
Our goal is the derivation of formulae describing the gravitation force as a recoil force caused by anisotropic emission of radiation. We start with the hypothesis that baryonic matter having the property of a mass exists in a dynamic equilibrium with the Quantum Vacuum (QV). The QV is a medium with extremely high energy density. This can be shown starting with Planck’s formula
![]() , (C1)
, (C1)
which defines the frequency domain energy distribution of thermal radiation. h is the Planck constant, k―the Boltzman c., T―the absolute temperature and f the frequency of radiation. The term hf/2 represents the zero- point fluctuations of QV. For T = 0 we get
![]() . (C2)
. (C2)
The total energy density in the frequency band from f1 to f2 is given by the integral
![]()
Figure 8. An infinite plane covered with a uniform surface mass density rm [kg/m2].
![]()
Figure 9. Two parallel planes of Figure 8. The two fields cancel inside but do not annihilate.
![]()
Figure 10. The shift of the left plane enlarges the volume without the g-field. The cancellation of the g-field requires an input of positive energy since the planes attract. Therefore the energy of the cancelled field is negative. The same evidence is given by calculation of the energy of the g-field of the spherical body of Figure 3. If for a mass 2M this energy equals E then for two bodies of a mass M this energy for each body equals E//4, i.e. one half of E is cancelled. The separation of these bodies shifting one body to infinity requires an input of positive energy. Evidently the cancelled energy is negative.
![]() . (C3)
. (C3)
Planck suggested that the highest frequency of the radiation is defined by the formula
![]() . (C4)
. (C4)
This value of f2 with f1 = 0 yields a formidable energy density of QV
![]() (C5)
(C5)
This value applies for a pure vacuum. In case of an electrostatic field ![]() the energy of the vacuum is given by the formula
the energy of the vacuum is given by the formula
![]() (C6)
(C6)
At the actual state of the art it is impossible to extract from the vacuum the energy EQV. Of course the energy of the electrostatic field can be used for any application. For example, charged capacitors can drive electric ma-
chines. In the case of a gravitational field ![]() the energy of the vacuum is given by the formula
the energy of the vacuum is given by the formula
![]() (C7)
(C7)
The negative sign shows that the g-field lowers the energy density of QV. The evidence is simple. The enlarging the distance between two parallel planes which cancels the g-field in certain volume requires an input of positive energy.