Spherical Casimir Effect for a Massive Scalar Field on the Three Dimensional Ball ()
1. Introduction
The electromagnetic Casimir effect was first predicted theoretically by H. G. B. Casimir [1] in 1948, when he showed that an attractive force exists between two electrically neutral, parallel conducting plates in vacuum. Boyer predicted the repulsive Casimir force some time later, when he discovered that a perfectly conducting, neutral spherical surface in vacuum modifies the vacuum energy of the electromagnetic field in such a way that the spherical surface is subject to an outward pressure [2] . Experimental confirmation of the Casimir effect came more than fifty years ago by Sparnaay [3] , and many improved experimental observations have been reported throughout the years [4] [5] .
Since their discovery, Casimir forces have been found to have many applications from nanotechnology to string theory, and a large effort has gone into studying the generalization of the Casimir effect to quantum fields other than the electromagnetic field: fermions were first considered by Johnson [6] then investigated by many others, and bosons and other scalar fields have also been investigated extensively [4] .
It is well known that Casimir forces are very sensitive to the boundary conditions of the quantum fields at the plates. In the case of scalar fields, Dirichlet and Neuman boundary conditions are most commonly used, in the case of fermion fields or other fields with spin [7] , bag boundary conditions are used. In this manuscript I investigate a scalar field that obeys Dirichlet boundary conditions on a spherical surface of radius a. While this paper investigates scalar fields within the context of a spherical geometry, the techniques that will be used in this paper can be extended to the case of other types of fields, such as fermions satisfying bag boundary conditions on the sphere. In the case of the parallel plates geometry, this extension to fermions was done in Ref. [8] . Another extension or application of this work could be within the context of the recent tests for the gravitational behavior of anti-matter, or antigravity experiments [9] . This paper could help understanding the phenomenon of quantum reflection of antimatter from spherical surfaces. This effect is relevant for the plate geometry to experi- ments such as GBAR where ultracold antihydrogen atoms are detected by annihilation on a plate ( [9] and re- ferences within).
Massive or massless scalar fields appear in many areas of physics from the Higgs field in the Standard Model, to the dilaton field that breaks the conformal symmetry in string theory, to the Ginzburg-Landau scalar field in superconductivity, etc.
The Casimir effect due to a scalar field has been studied extensively in the parallel plate and spherical geometry. Different regularization techniques have been used to remove the singularities of the Casimir energy such as, for example, the zeta function technique and the Casimir piston technique. While in the context of this work I will use the zeta function technique, the Casimir piston technique [10] - [12] is quite intriguing, being physically more direct in the case of the parallel plates geometry and, in the future, the Casimir spherical piston technique should be investigated.
The spherical Casimir effect for massless [13] [14] or massive [15] - [18] scalar fields in 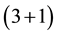 or
or  dimensions has been studied in vacuum and at finite temperature [19] [20] using the Green’s function method [13] [17] , the zeta function technique [14] - [16] [18] and the heat kernel expansion [21] - [23] to calculate the Casimir energy. These authors however, are only able to obtain the Casimir energy for large scalar mass as an infinite sum of hypergeometric functions. In this manuscript I use the zeta function technique to study the spherical Casimir effect for a scalar field of mass m and, without using the heat kernel expansion, obtain simple analytic forms for the zeta function and Casimir energy when the scalar field is confined inside or outside the spherical surface, in the case of large scalar mass
dimensions has been studied in vacuum and at finite temperature [19] [20] using the Green’s function method [13] [17] , the zeta function technique [14] - [16] [18] and the heat kernel expansion [21] - [23] to calculate the Casimir energy. These authors however, are only able to obtain the Casimir energy for large scalar mass as an infinite sum of hypergeometric functions. In this manuscript I use the zeta function technique to study the spherical Casimir effect for a scalar field of mass m and, without using the heat kernel expansion, obtain simple analytic forms for the zeta function and Casimir energy when the scalar field is confined inside or outside the spherical surface, in the case of large scalar mass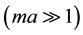 . In both cases the Casimir energy is found to be divergent, as expected [15] [16] . I also obtain simple expressions for the large mass Casimir energy and force on the spherical surface in the case of a scalar field present both inside and outside the spherical surface. The energy and force obtained for this scenario are finite and differ from results obtained previously by authors that used the heat kernel expansion.
. In both cases the Casimir energy is found to be divergent, as expected [15] [16] . I also obtain simple expressions for the large mass Casimir energy and force on the spherical surface in the case of a scalar field present both inside and outside the spherical surface. The energy and force obtained for this scenario are finite and differ from results obtained previously by authors that used the heat kernel expansion.
In Section 2, I describe the model and, for the case of a scalar field confined inside the spherical surface, obtain the zeta function 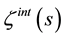 using the Debye uniform asymptotic expansion of the modified Bessel functions. In Section 3, I find a simple expression for
using the Debye uniform asymptotic expansion of the modified Bessel functions. In Section 3, I find a simple expression for 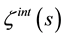 in the large mass limit. In Section 4, I use the large mass limit of
in the large mass limit. In Section 4, I use the large mass limit of 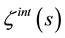 to calculate the Casimir energy for a scalar field confined inside the spherical surface, in the case of
to calculate the Casimir energy for a scalar field confined inside the spherical surface, in the case of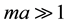 . I also obtain, using
. I also obtain, using 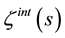 from Section 3, the large mass limit of the zeta function and Casimir energy in the case of a scalar field confined outside the spherical surface. Finally I study the case of a scalar field present both inside and outside the spherical surface, and find very simple analytic expressions for the Casimir energy and force on the spherical shell, when
from Section 3, the large mass limit of the zeta function and Casimir energy in the case of a scalar field confined outside the spherical surface. Finally I study the case of a scalar field present both inside and outside the spherical surface, and find very simple analytic expressions for the Casimir energy and force on the spherical shell, when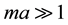 . A summary and discussion of my results are presented in Section 5.
. A summary and discussion of my results are presented in Section 5.
2. Zeta Function inside a Spherical Surface
In 3-dimensional space the equation of motion of a scalar field, 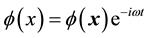 , is the Klein-Gordon equation
, is the Klein-Gordon equation
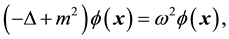
where m is the scalar field mass. Using spherical coordinates, this equation becomes
![]() (1)
(1)
where ![]() is the angular momentum operator. After a separation of variables
is the angular momentum operator. After a separation of variables
![]()
the radial part of Equation (1) is found to be
![]() (2)
(2)
A complete set of solutions of Equation (2), finite at the origin, is
![]()
where ![]() are Bessel functions of the first kind and
are Bessel functions of the first kind and![]() . Once we impose Dirichlet boundary conditions on a spherical surface of radius a
. Once we impose Dirichlet boundary conditions on a spherical surface of radius a
![]()
we find
![]()
where ![]() is the n-th zero of
is the n-th zero of ![]() and
and![]() . The energy eigenvalues are found immediately
. The energy eigenvalues are found immediately
![]()
and, when the scalar field is confined inside the spherical surface, the zeta function is given by
![]() (3)
(3)
where ![]() is the degeneracy of the eigenmodes of angular momentum l.
is the degeneracy of the eigenmodes of angular momentum l.
Since ![]() has simple poles at
has simple poles at![]() , I can write Equation (3) in the form of a contour inte- gral [21] [22]
, I can write Equation (3) in the form of a contour inte- gral [21] [22]
![]()
where the closed contour ![]() runs counterclockwise, contains the whole positive k-axis and, with it, all of the
runs counterclockwise, contains the whole positive k-axis and, with it, all of the
![]() for
for ![]() and
and![]() . Next I rotate the integration contour to the imaginary axis and obtain
. Next I rotate the integration contour to the imaginary axis and obtain
![]() (4)
(4)
where![]() ,
, ![]() is a modified Bessel function of the first kind, and the added factor
is a modified Bessel function of the first kind, and the added factor ![]() inside the
inside the
logarithm does not change the result, since no additional pole is enclosed. A simple change of the integration variable allows me to rewrite Equation (4) as
![]() (5)
(5)
and to exploit the Debye uniform asymptotic expansion of the modified Bessel functions [15]
![]() (6)
(6)
where
![]()
and ![]() is defined recursively by
is defined recursively by
![]()
I use Equation (6) and find
![]() (7)
(7)
where the ![]() are defined through
are defined through
![]()
and are polynomials of degree 3i
![]()
while the coefficients ![]() can be easily calculated with a simple computer program. It is clear that, as N grows, the right side of Equation (7) becomes a more accurate approximation of the left side of (7). Using Equation (7), I write the following approximate expression of the zeta function
can be easily calculated with a simple computer program. It is clear that, as N grows, the right side of Equation (7) becomes a more accurate approximation of the left side of (7). Using Equation (7), I write the following approximate expression of the zeta function
![]() (8)
(8)
with
![]() (9)
(9)
![]() (10)
(10)
and, for ![]()
![]() (11)
(11)
Equation (8) displays the same feature as Equation (7): as N grows the sum on the right side becomes a more accurate approximation of the zeta function. Notice that the coefficients ![]() of Equations (9)-(11) are defined in the same way as in [15] . Notice also that the authors of Ref. [15] use only the first five of the
of Equations (9)-(11) are defined in the same way as in [15] . Notice also that the authors of Ref. [15] use only the first five of the![]() , ending the sum at
, ending the sum at![]() , and therefore need to add a term,
, and therefore need to add a term, ![]() , that can only be evaluated numerically with considerable numerical challenges, since
, that can only be evaluated numerically with considerable numerical challenges, since ![]() is defined as the difference of integrals whose values are nearly identical and many orders of magnitude larger than their difference. The alternative approach presented in this work ends the sum in Equation (8) at
is defined as the difference of integrals whose values are nearly identical and many orders of magnitude larger than their difference. The alternative approach presented in this work ends the sum in Equation (8) at![]() , with N high enough that one does not need to add a numerical term to Equation (8).
, with N high enough that one does not need to add a numerical term to Equation (8).
3. Zeta Function in the Large Mass Limit
In this section I evaluate the ![]() of Equation (8) in the limit
of Equation (8) in the limit![]() , using a simpler and more direct method than the heat kernel expansion. At this stage, since the lower limit of integration in the three integrals (9 - 11) is very large, I use a large z asymptotic expansion of their integrands. When
, using a simpler and more direct method than the heat kernel expansion. At this stage, since the lower limit of integration in the three integrals (9 - 11) is very large, I use a large z asymptotic expansion of their integrands. When![]() , I can write
, I can write
![]()
and therefore, in the large mass limit, I find
![]() (12)
(12)
Similarly
![]()
![]()
![]()
when![]() , and thus
, and thus ![]() and
and ![]() become
become
![]() (13)
(13)
![]() (14)
(14)
After I change the integration variable from z to ![]() in the integrals of Equations (12)-(14), use
in the integrals of Equations (12)-(14), use
![]()
and integrate over the new variable y, I obtain
![]()
![]()
and, for ![]()
![]()
The integrals over ![]() are done easily, and I find
are done easily, and I find
![]() (15)
(15)
![]() (16)
(16)
and, for ![]()
![]() (17)
(17)
where
![]()
is the Hurwitz zeta function.
4. Casimir Energy and Force in the Large Mass Limit
The Casimir energy for a massive scalar field confined inside a spherical surface of radius a, is given by
![]()
where ![]() is given by Equation (8), and therefore I obtain the large mass limit of
is given by Equation (8), and therefore I obtain the large mass limit of ![]() using Equations (15)-(17) for the large mass limits of the
using Equations (15)-(17) for the large mass limits of the![]() . I find
. I find
![]() (18)
(18)
for![]() , where
, where ![]() is the Riemann zeta function of number theory and
is the Riemann zeta function of number theory and ![]() is the Euler
is the Euler
Mascheroni constant, and where I neglected all terms of order ![]() with
with![]() , since
, since![]() . Similarly, I find
. Similarly, I find
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
where I used![]() ,
, ![]() , and neglected all terms of order
, and neglected all terms of order ![]() with
with![]() . The expansions of the
. The expansions of the
![]() derived in Equations (18)-(21) are different from those obtained by other authors [15] . Notice that, since
derived in Equations (18)-(21) are different from those obtained by other authors [15] . Notice that, since
the contribution of ![]() is of order
is of order![]() , I do not need to consider any
, I do not need to consider any ![]() with
with![]() , and there- fore the exact large mass limit of
, and there- fore the exact large mass limit of ![]() to order
to order ![]() is
is
![]() (22)
(22)
where the ![]() are given by Equations (18)-(21). Notice also that, as
are given by Equations (18)-(21). Notice also that, as![]() , the expected diver- gencies [15] only appear in
, the expected diver- gencies [15] only appear in ![]() and
and![]() , due to the factors of
, due to the factors of ![]() and
and ![]() present inside Equ- ations (15) and (17). All the other
present inside Equ- ations (15) and (17). All the other ![]() are free of divergencies as
are free of divergencies as![]() , since
, since ![]() is finite when
is finite when
![]() and
and![]() . This result for the Casimir energy is different from the one obtained using the heat kernel method [15] [23] .
. This result for the Casimir energy is different from the one obtained using the heat kernel method [15] [23] .
The appearance of divergencies in the calculation of ![]() requires renormalization of the Casimir energy, and I will use the same renormalization procedure presented first in Ref. [15] . The physical system examined in this paper consists of a classical and a quantum part. The classical part is a spherical surface of radius a with energy
requires renormalization of the Casimir energy, and I will use the same renormalization procedure presented first in Ref. [15] . The physical system examined in this paper consists of a classical and a quantum part. The classical part is a spherical surface of radius a with energy
![]()
where ![]() is the volume, p is the pressure,
is the volume, p is the pressure, ![]() is the surface,
is the surface, ![]() the surface tension and F, k,
the surface tension and F, k,
and h do not have names. The quantum part of the system under consideration is a scalar field satisfying Dirichlet boundary condition on the spherical surface. The ground state energy of this scalar field, ![]() , is divergent and will be renormalized following the scheme described in [15] : divergent contributions to
, is divergent and will be renormalized following the scheme described in [15] : divergent contributions to ![]() will be subtracted by means of a renormalization of the corresponding parameters in
will be subtracted by means of a renormalization of the corresponding parameters in![]() . This renormalization is achieved by shifting the parameters in
. This renormalization is achieved by shifting the parameters in ![]() by an amount which cancels the contributions of the two co-
by an amount which cancels the contributions of the two co-
efficients ![]() and
and![]() , that diverge as
, that diverge as![]() . The two parameters in
. The two parameters in ![]() that need to be shifted
that need to be shifted
are F and h, since ![]() and
and![]() .
.
If the scalar field is confined outside the spherical surface, the zeta function is [15]
![]() (23)
(23)
and can be used to calculate![]() , the Casimir energy for the exterior region. The large mass limit of
, the Casimir energy for the exterior region. The large mass limit of![]() ,
,
exact to order![]() , is
, is
![]() (24)
(24)
with the ![]() given by Equations (18)-(21). Since
given by Equations (18)-(21). Since ![]() and
and ![]() contain divergent
contain divergent
terms as![]() , the Casimir energy for the exterior region is also divergent, as expected, but different from the one obtained in Refs. [15] [23] . The renormalization of the divergent Casimir energy
, the Casimir energy for the exterior region is also divergent, as expected, but different from the one obtained in Refs. [15] [23] . The renormalization of the divergent Casimir energy ![]() can be carried out using the same procedure outlined above for
can be carried out using the same procedure outlined above for ![]() [15] .
[15] .
Finally, I discuss the situation where the scalar field is present in both the interior and exterior regions. In this case the Casimir energy is
![]()
and, using Equations (22) and (24), I find a finite value for the large mass limit of E
![]() (25)
(25)
again different from what appears in the literature [5] . Notice that, as![]() , the Casimir energy
, the Casimir energy![]() . The Casimir force F on the spherical surface of radius a is given by
. The Casimir force F on the spherical surface of radius a is given by
![]()
and I find a repulsive force
![]() (26)
(26)
indicating an outward pressure on the spherical surface, that vanishes as![]() . The large mass limit Casimir
. The large mass limit Casimir
energy E and force F that I find in Equations (25) and (26), are exact to order ![]() and
and ![]() respectively.
respectively.
5. Discussion and Conclusions
In this manuscript I used the zeta function regularization technique to study the spherical Casimir effect of a massive scalar field in ![]() dimensions. I analyzed three scenarios: a scalar field confined inside a spherical surface, a scalar field confined outside the spherical surface, and a scalar field present inside and outside the spherical surface at the same time. In all cases Dirichlet boundary conditions were imposed on the sphere of radius a. I obtained two expressions of the zeta function in the large mass limit, one valid inside the sphere and
dimensions. I analyzed three scenarios: a scalar field confined inside a spherical surface, a scalar field confined outside the spherical surface, and a scalar field present inside and outside the spherical surface at the same time. In all cases Dirichlet boundary conditions were imposed on the sphere of radius a. I obtained two expressions of the zeta function in the large mass limit, one valid inside the sphere and
one valid outside, which are exact to order![]() , and used them to obtain the large mass limit of the Casimir energy inside (22) and outside the sphere (24), exact to order
, and used them to obtain the large mass limit of the Casimir energy inside (22) and outside the sphere (24), exact to order![]() . These Casimir energies contain diver-
. These Casimir energies contain diver-
gencies, as I expected, and can be renormalized following the renormalization procedure described in Ref. [15] , but disagree with the values calculated in previous papers that use the heat kernel expansion [5] [15] [23] .
Finally, I studied the case of a scalar field present both inside and outside the spherical surface, and obtained the large mass limit of the Casimir energy (25) and force (26) in this case. Both quantities are finite and thus do
not need to be renormalized, and are exact to order ![]() and
and ![]() respectively. Also these results do not agree with previously published results [5] [15] [23] .
respectively. Also these results do not agree with previously published results [5] [15] [23] .
For a scalar field with mass![]() , such as the Higgs, I find that any spherical surface of radius
, such as the Higgs, I find that any spherical surface of radius![]() , with
, with![]() , abundantly satisfies the large mass condition, since
, abundantly satisfies the large mass condition, since![]() . In this scenario, I find that the Casimir force on the spherical surface is
. In this scenario, I find that the Casimir force on the spherical surface is![]() , where
, where ![]() is obtained by using
is obtained by using ![]() and
and ![]() in Equation (26).
in Equation (26).