Global Solar Variations and Effects of Relativistic 2D-Hydrogen ()
1. Introduction and Previous Work
1.1. Solar Activity and Fundamental Harmonics
Utilization of fundamental harmonics, the integer doubling or halving of a previous cycle, clearly showed that the distribution of the normalized geophysical and astronomical cycles displayed a central mode of approximately 11 years known as the Schwabe cycle, with two side modes just within plus or minus one standard deviation [1] [2] . Based on this central period C* it was shown that its relationship to any cycle C as reported in the literature on time scales of years to minutes could be expressed by a harmonic progression of the form
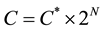 , where N is an integer (−N, 0, N) (1)
, where N is an integer (−N, 0, N) (1)
The significance of this far reaching concept is found in the fact that it results from the most basic physical process operating in the Sun, thermonuclear fusion in the energy generating region. In fact, the construct of a solar output model [3] involving the superposition of various cycles proved to exhibit a pattern consistent with nuclear magnetic resonance NMR of 1H and 3He in the solar core (Bethe/Weizäcker core). Due to the nuclear magnetic moments NMM of the isotopes in the fusion chain with 1H having the strongest positive NMM, the fusion events of 1H and 3He, would release varying amounts of energy, with NMR being a controlling factor as nuclei in a magnetic field absorb and re-emit electromagnetic radiation energy. It was hypothesized that the pulses of energy from magnetically synchronized fusion events at NMR-frequencies are transformed into pressure waves that may be the basis for other solar oscillations.
Furthermore it was found that superimposed NMR frequencies of 1H and 3He, F(1H)NMR and F(3He)NMR result in beat frequencies Fbeat yielding periods of about 8 to 14 years or about 4 to 6 minutes in a varying field of a few Gauss and harmonic up to N = 43. Of particular interest is to find a beat frequency termed optimum Fbeat for the Schwabe cycle of ~11 years (period 10.6 years [4] ), and the acoustic p-mode oscillation of ~5.5 minutes near 7 - 8 Gauss, all based entirely on the fundamental harmonic progression. These beat frequencies or synchronous oscillations in the range of either years or minutes, originating within the energy generating region, leave their detectable signal in the form of global oscillations, and may be considered the actual controlling factor of solar variability via pressure and gravity waves.
In fact, some of the earliest highly precise, very low background noise, measurements of global solar oscillations were conducted in Antarctica at the South Pole by Pomerantz et al. [5] . They found that the characteristics of the spectrum of solar acoustic modes having periods of around 5 minutes, represented spherical harmonics of degree ranging from 0 to 100. Continuing the work at the South Pole, the group Jeffries et al. [6] reported the astonishing result that “the frequency spectrum of the solar oscillations contains many millions of different modes between roughly 3 and 15 minutes, showing that helioseismology plays a major role in understanding stellar structure and evolution”.
1.2. A 2-Step Signature of the Solar Magnetic Field, Fundamental Pattern
In an evaluation of the solar magnetic field spanning ~300 years, a model of reconstructed total flux [7] , it was found that the temporal evolution of the field showed a striking pattern of the minimum values (Bmin) relative to the maximum values (Bmax) per Schwabe cycle which seemed to follow a 2-step response of the system [4] .
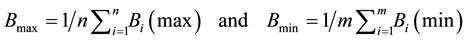 (2)
(2)
where n, m are the number of maxima and minima, respectively, per group.
This 2-step pattern resembles variations between sequential states of equilibrium of the quiet Sun termed group one (I) to six (VI), each group extending over several (average ~4) Schwabe cycles (~11 years), with approximate equal minimum values being maintained per group. The step-like behavior shows increasing magnetic field strength B with decreasing cycle length as expected. However, with group VI representing the modern era it is associated with the highest magnetic field value but not the highest energy level in terms of group cycle length. In fact, when not considering the absolute values Bmax and Bmin, but their ratios BR
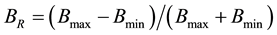 (3)
(3)
and plotted again against the average cycle length per group, shown in Figure 1 [4] for all group periodicities (~8 to ~12 years), a cluster of three groups is found near the periodicity of ~11 years, for group VI the periodicity is very close to the central position of 10.6 years, the optimum period as found in Section I.1, which has also been reported as a strong peak in the aa-index power spectrum [8] . It allows to conclude that the 2-step mode is part of a consistent pattern of fundamental harmonic progression consistent with C = C* × 2N. Therefore, the temporal evolution of the solar magnetic field as derived from the data above in conjunction with the presence of fundamental harmonic progression, based on the quantity NMR-Fbeat inherent to the energy generating region of the sun, can be seen as being supported in light of the periodic components found to propagate through the
![]()
Figure 1. The 2-step association of BR of group I to VI plotted against group cycle length. Three groups cluster around the ~11-year periodicity as outlined by broken bars, averaging 10.6 years represented by group VI (adapted from [4] ).
IMF as reported by Thomson et al. [9] . In fact, from the results of the measured spectrum and its evaluation it was determined that the periodic variations seen in the interplanetary medium as represented by
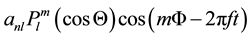 (4)
(4)
are of solar origin and are pressure and gravity modes with periods varying from 4 to 20 minutes or >40 minutes. (f frequency of oscillation, anl amplitude with spherical harmonic degree l and radial order n, 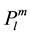 Legendre polynomial of azimuthal order m, see Christensen-Dalsgaard et al. [10] ). In his comments Gough [11] pointed out that it was unexpected that such periodic components or coherent seismic oscillations of the sun were detectable in the IMF in view of the many difficulties that were to be expected in traversing a medium with inhomogeneities and turbulence such as the chromosphere, the corona and further out in the heliosphere as well. However, it is important to realize that in part fluctuations in the IMF are possibly the result of large-scale Alfvén waves propagating into the heliosphere with amplitudes of the solar modes expected to last relatively long periods of time [9] .
Legendre polynomial of azimuthal order m, see Christensen-Dalsgaard et al. [10] ). In his comments Gough [11] pointed out that it was unexpected that such periodic components or coherent seismic oscillations of the sun were detectable in the IMF in view of the many difficulties that were to be expected in traversing a medium with inhomogeneities and turbulence such as the chromosphere, the corona and further out in the heliosphere as well. However, it is important to realize that in part fluctuations in the IMF are possibly the result of large-scale Alfvén waves propagating into the heliosphere with amplitudes of the solar modes expected to last relatively long periods of time [9] .
Whereas current knowledge about the deep interior of the sun imposes a severe limit on a quantitative understanding of energy transfer from the source of energy to the convection zone on time scales shorter than the photon diffusion time scale of almost a million years, this work focuses on the process of activity variation based on systematic long-term behavior as coherent oscillations on the surface of the sun. Furthermore, since it has been found to be traceable to a simple, fundamental quantity NMR-Fbeat originating with the thermonuclear process within the solar core region, the resulting pressure waves, permeating the entire solar body and further propagating throughout the heliosphere, ultimately leading to solar activity variation in general.
It can be assumed to be most likely a major contributing factor to steep gradients of pressure and temperature in localized areas and ultimately near the surface as well, Δp and ΔT, with consequences for the quantum state of hydrogen and helium as discussed in the following Sections 2.
2. Effects of Dimension Reduction
2.1. Relativistic 2D Hydrogen
Thermodynamic conditions vary greatly along the sun’s radius, however, pressure wave oscillations may provide density variations throughout the solar body with severe consequences within very localized zones, on a scale of the reduced mass of proton and electron, where the electron becomes relativistic within its local 2D con- finement. Therefore we conjecture that in such localized areas 2-dimensional conditions can arise within the plasma environment of the sun, simply due to continuous pressure wave variation, where the possibility exists for protons and electrons to form a semion or near semion state. This quantum state is expected to exist because such a probability is based on theoretical work [12] [13] where it was shown that exact analytical solutions for 2D hydrogen can be derived, i.e. for the non-relativistic and the relativistic H-atom with significant changes to the eigenfunctions and eigenvalues.
Therefore, in a zone, where hydrogen and helium would effectively be confined in a 2-dimensional space, in other words where according to such boundary conditions the Bohr-atom model would become 2-dimensional, i.e. the electron orbits of the hydrogen and helium atoms are expected to be confined in a 2-dimensional plane [14] . At the same time this constraint does not apply to all other fields such as electromagnetic fields, photon emission, angular momentum, and spin [12] . Therefore, the loss of a single space dimension would affect the quantum states significantly. Here we propose to consider such zones in addition to an extension of such conditions to a sub-photosphere-layer in terms of the role of 2D effects on symmetry in 3D.
Inherent to 2D relativistic conditions of the H-atom is the presence of the Chern-Simons vector potential field. Some detail of the 2D relativistic hydrogen problem is discussed in ([14] , chapter 3). The relativistic Hamiltonian for an electron placed in the Coulomb potential V(r) created by the proton is expressed by
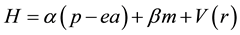 (5)
(5)
where m is the reduced mass between the electron and the positive nucleus, α and β are matrices, p momentum, a the Chern-Simons potential field. This Chern-Simons potential field in Equation (5) is a non-parity conserving term due to the decoupling of spin-up and spin-down states. Such a term in the field theoretical language corresponds to the Chern-Simons gauge field.
Here we point out that the significance of 2D-confinement is that dimension reduction from 3D to 2D can introduce unexpected changes in the contribution of the vector potential to the electron. In fact because of the Chern-Simons gauge field the exact solutions show for the relativistic ground state binding to become as large as the reduced mass [13] , in other words, the binding energy plus the rest energy can become zero if the attraction center’s positive charge is much more massive than the electron. In such a case a hydrogen atom can approach a Semion state or it becomes a collapsed hydrogen atom. With these atoms being fully relativistic the binding ground state energy of the 2D relativistic hydrogen [13] is given by
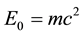 (6)
(6)
where m is the reduced mass of the electron and the positive nucleus.
In other words, if the ground state of the relativistic hydrogen becomes as large as  = 0.5 MeV then photo emission from ionization would be close to the 0.5 MeV energy level. In terms of being able to observe such emission lines at the surface, the difficulty lies in the fact that the signal may be obscured due to the electron/positron annihilation 0.5 MeV single line.
= 0.5 MeV then photo emission from ionization would be close to the 0.5 MeV energy level. In terms of being able to observe such emission lines at the surface, the difficulty lies in the fact that the signal may be obscured due to the electron/positron annihilation 0.5 MeV single line.
Nevertheless we may consider the example of hydrogen and helium being localized in a 2D layer below and near the photosphere.
If we treat 3He like the 2D hydrogen, then the ground state binding energy for the second electron can also be expressed by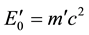 , where
, where 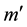 is the effective reduced mass. The reduced masses for these two cases (1H and 3He) are
is the effective reduced mass. The reduced masses for these two cases (1H and 3He) are
 (7)
(7)
where mp, mn, and me are the rest masses of a proton, a neutron and an electron respectively. Thus the ionization energies by photon absorption for these cases are different. In fact, it takes more energy to ionize the 3He then the hydrogen. This difference can be calculated to be 185 eV.
The amount of energetic photons available for the ionization depends on the temperature where the ionization occurs. Within the solar body this would be a continuous creation and destruction process. However, near the surface it is expected that these two events must occur at different depths from the solar surface, with hydrogen being ionized nearer to the surface than 3He. In 3D space the photon energies released from their ionization are indistinguishable, whereas when the isotopes 3He, 4He, and 1H are confined in a 2D space environment, then their electron binding energy being given by the rest mass energy will result in a ΔE difference of the order of hundredth of eV. However, it is realized that detecting the separate lines of the photo emission from these three ionizations would not have a high probability, because they are all in the range of half a MeV and cannot easily be distinguished being close to the single line of electron/positron annihilation.
2.2. 2D Relativistic Hydrogen, Magnetic Contributions to the Solar Global Dipole Field?
Considering further the concept of the 2D effect, we will consider a phenomenological description of the magnetic phenomena associated with the planar hydrogen atom within a 2D environment or layer. The Chern- Simons ground state conditions involve the occurrence of a very small gauge confinement radius producing a very strong loop current and in turn a very strong magnetic moment.
Since magnetic activity as expressed by harmonic progression detected in solar activity variations, was found to be a consequence of solar global oscillations resulting from the optimum NMR-frequencies of the core constituents leading to the well known ~11 yr and ~5 min periods, and detected as coherent seismic waves in the heliosphere [9] , a 2D-sub-surface-layer, if it exists, clearly must take part in such non-random variations. It means that 2D relativistic H-atoms together with the 2D 3He-atoms are the participants in pressure oscillation fields as observed for the photosphere. Of course, the requirement and justification for having 2D H-atoms present close to the surface is a sub-photospheric layer or zone, and inherent to the 2D conditions of the H-atom is the presence of the additional Chern-Simons vector potential which is part of the solution of the radial Schrödinger equation for the relativistic 2D H-atom which results in the very large ground state binding energy of 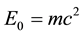 = 0.5 MeV (m = reduced mass) as pointed out above. In such a configuration the planar, non- ionized, H-atom will exhibit a magnetic moment aligned with Δp, ΔT, i.e. a radial magnetic field
= 0.5 MeV (m = reduced mass) as pointed out above. In such a configuration the planar, non- ionized, H-atom will exhibit a magnetic moment aligned with Δp, ΔT, i.e. a radial magnetic field 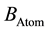 which in turn will contribute to the solar global dipole field
which in turn will contribute to the solar global dipole field 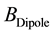 as indicated in Figure 2 with a simple sketch, which indicates the probability for some strengthening or weakening of the dipolar magnetic field with latitudinal
as indicated in Figure 2 with a simple sketch, which indicates the probability for some strengthening or weakening of the dipolar magnetic field with latitudinal
dependence. As indicated in superposition or coupling within the stratified 2D confinement can be expressed in first approximation using the geometric interpretation of the dot product![]() . Although ultimately latitudinal effects on coupling of nearest neighbors within the 2D confinement would also have to be considered because they are expected to be a function of density and temperature. In principle, however, if temperature and pressure are periodic then the coupling is periodic, which is a given due to the principle of harmonic progression of energy i.e. pressure wave propagation from the core to the surface, which results in a non-random, i.e. coherent, ordered periodicities expressed by Equation (1). The end result is coherency with the sum of all fields, where “pumping” with the proper resonance frequency may induce a crucial condition which can be achieved and maintained. In other words, it allows for a “quantum state” to be maintained beyond some critical value, in this case a critical magnetic field strength Bc, i.e. via the optimum frequencies ~10.6 yr and ~5 min, and with it the relativistic 2D H-atom population can be maintained over some period of time. However, when entanglement (density dependent corresponding to Δp, ΔT) in the 2D layer reaches or exceeds a critical value in momentum and density such a unit can collapse onto itself, meaning a state of instability is reached.
. Although ultimately latitudinal effects on coupling of nearest neighbors within the 2D confinement would also have to be considered because they are expected to be a function of density and temperature. In principle, however, if temperature and pressure are periodic then the coupling is periodic, which is a given due to the principle of harmonic progression of energy i.e. pressure wave propagation from the core to the surface, which results in a non-random, i.e. coherent, ordered periodicities expressed by Equation (1). The end result is coherency with the sum of all fields, where “pumping” with the proper resonance frequency may induce a crucial condition which can be achieved and maintained. In other words, it allows for a “quantum state” to be maintained beyond some critical value, in this case a critical magnetic field strength Bc, i.e. via the optimum frequencies ~10.6 yr and ~5 min, and with it the relativistic 2D H-atom population can be maintained over some period of time. However, when entanglement (density dependent corresponding to Δp, ΔT) in the 2D layer reaches or exceeds a critical value in momentum and density such a unit can collapse onto itself, meaning a state of instability is reached.
As to the appearance and stability of the 2D sub-photosphere conditions it is clear that temperature perturbations must play a role, and as discussed by Kuhn [15] there may be an internal non-spherical solar temperature structure. In fact a pole-equator difference in effective temperature is inferred [16] . In addition, however, Gough questions a possibility as well, namely that there may be a deep-seated origin of the solar cycle. We constrain ourselves to the most straightforward assumptions providing a simple model because the F(beat) frequencies 11 yr/5min periods are the major consistent drivers of measured solar activity present in geophysical records. For this reason our concern are the low degree mode oscillations which make possible the traversing of the solar body from great depth, and therefore allow information to be gained from the deep interior including the core.
In fact, since we may say the sun is beating with the optimum frequencies where![]() ; C* = 11 yr or 5 min; and since 2 hemispheres are involved as to the
; C* = 11 yr or 5 min; and since 2 hemispheres are involved as to the ![]() effect, the contribution of the 2D layer to the 11/22 yr variation may be quite substantial. The degree of magnetic field variation may be not unlike the effect described by Nesme-Ribes et al. [17] where the effect of the interaction of the dipole/quadrupole is invoked. For example, a weak quadrupole field “beating” in phase with the dipole would lead to short and intense cycles, whereas a strong quadrupole would lengthen and weaken the sunspot cycle.
effect, the contribution of the 2D layer to the 11/22 yr variation may be quite substantial. The degree of magnetic field variation may be not unlike the effect described by Nesme-Ribes et al. [17] where the effect of the interaction of the dipole/quadrupole is invoked. For example, a weak quadrupole field “beating” in phase with the dipole would lead to short and intense cycles, whereas a strong quadrupole would lengthen and weaken the sunspot cycle.
Recent research and a number of discoveries of solar phenomena do not seem to contradict any of our conjecture, e.g. small-scale magnetic flux on the quiet sun detected by making use of the quantum mechanical Hanle effect as described by Trujillo Bueno et al. [18] , where the signature may contain the effects from granulation and small-scale magnetic flux present on the quiet sun and may reveal an additional contribution to the general global solar magnetic field, not revealed by the Zeeman effect. Based on work by De Pontieu et al., [19] , particularly the quiet Sun may contribute significantly to the efficiency of photospheric oscillations driving mass flow into the chromosphere, and has been more clearly summarized by stating “that p-modes are crucial: on inclined magnetic flux tubes the p-modes leak sufficient energy from the global resonant cavity into the chromosphere to power shocks, that drive upward flows and form spicules”.
More recently the IRIS project, examining the interface region, photosphere-solar atmosphere, includes the uncovering of small-scale, but high-speed jets ejected from the surface (De Pontieu et al., [20] ). Let us expand our conjecture about the characteristic of the 2D sub-surface layer where the huge binding of the H-atom obviously is in 2D. If this 2D quantum state 2D solution is no longer valid due to boundary condition change, the 3D solution takes over. In the process very energetic gamma radiation is emitted.
3. Discussion and Conclusions
Two concepts at the base of this work as to conditions in a very hot, high pressure environment such as a star, i.e. the Sun, can be summarized as follows:
(1) Zones of 2D confinement of relativistic 2-dimensional hydrogen and hydrogen-like Chern-Simons ground states occur and
(2) such zones are affected and modulated by a system of global oscillations resulting from NMR processes associated with the thermonuclear fusion in the energy generating region of the core, as well as exhibiting a progression cycle of multiples of 2N based on the photo radiation associated with 2D hydrogen or hydrogen-like Chern-Simons ground states.
Regardless of the ultimate state of the relativistic hydrogen throughout the solar body, radial magnetic field contributions as well as the large binding energy in the range of 0.5 MeV within the 2D sub-surface-zones (see figure caption of Figure 2 on Chern-Simons gauge) will leave a signature under the modulation of global, coherent oscillations directly related to the optimum-beat frequencies corresponding to the observed 11 yr/5min periodicities of solar activity cycles. Furthermore, in view of the Chern-Simons ground state conditions where the gauge confinement radius is extremely small, it would produce a very strong loop current with in turn producing a very strong magnetic moment, perpendicular to the current of the planar atom. In addition, in terms of an observable signature, the 2D relativistic hydrogen can emit high energy gamma rays only if the dimensionality changes with the 3D ground state energy being far less than mc2.
On the other hand, the magnetic phenomena as expressed by harmonic progression and having been suggested to be associated with the deep interior of the sun, it is further suggested that the signature observed in geophysical records representing solar activity variations can be traced to a sequence of “facts” directly associated with global oscillations at the 11 year/5min level of low degree mode oscillations. For example 5 min oscillations of degree l = 7 as pointed out by Wolff [21] , specifically may have a ‘striking similarity’ of the shape of such g-modes with the occasional geometry of coronal holes (see example of coronal holes taken 5/27/2015, Figure 3). Since the structure of coronal holes is closely related to the solar wind as it propagates and is intimately associated with the temporal and spatial structure of the IMF, which in turn sets the stage for the open magnetic flux and therefore heliospheric magnetic conditions [22] , the signature transmitted from the interior, i.e. the solar core, via global coherent oscillations, may clearly be conjectured to be the driving force of all solar variability as detected in geophysical records. In this context it is important to realize that the open magnetic flux provides the largest contribution to the global solar magnetic field, the larger and smaller bipolar regions provide by far much less [23] .
As pointed out above in Section I these beat frequencies or synchronous oscillations in the range of either years or minutes, originating within the energy generating region, leave their detectable signal in the form of global oscillations, and may be considered the actual controlling factor of solar variability via pressure and gravity waves. Certain wavelengths, based on spherical harmonics, may reenter the solar interior to modulate the fusion process [24] , thereby contributing to perturbations resulting in apparent deviations from the “precise” chronometer with magnetically low episodes as found for solar type stars [25] .
On the other hand, the solar energy output as it is manifested in the detection of the periodicities within the interplanetary magnetic field, and as reflected in a long-term record of total magnetic flux as modeled by Solanki et al. [7] , for which the long-term temporal evolution was shown to exhibit an additional characteristic, which may have relevance in the current era. Dreschhoff [4] and Dreschhoff and Jungner [26] proposed a dimensionless quantity ![]() (see Figure 1), the ratio between maximum and minimum magnetic flux which was defined as “visibility”. Making use of this simple concept of magnetic flux emergence, plotted as a function of time as shown in Figure 4, the normalized data BR seem to reflect some type of amplitude and frequency modulated dampened oscillation over the approximate time span of ~300 years. It was inter-
(see Figure 1), the ratio between maximum and minimum magnetic flux which was defined as “visibility”. Making use of this simple concept of magnetic flux emergence, plotted as a function of time as shown in Figure 4, the normalized data BR seem to reflect some type of amplitude and frequency modulated dampened oscillation over the approximate time span of ~300 years. It was inter-
![]()
Figure 4. The ratios have been plotted as a function of time from 1750 to ~2000 (modern era). The temporal evolution of the six groups (see Figure 1) representing this time period shows that the amplitude variation of ![]() have the resemblance of a dampened oscillation, clearly showing the 2-step response of the system and where the final value of group VI represents the optimum cycle length of 10.6 yr.
have the resemblance of a dampened oscillation, clearly showing the 2-step response of the system and where the final value of group VI represents the optimum cycle length of 10.6 yr.
esting to point to the apparent downturn of the approximate end of high activity in both, Bmax and Bmin, during the modern era. This interpretation of possibly being the beginning of some extended minimum, seemed to be supported by the occurrence of a barrage of solar proton events preceding the Maunder Minimum [26] - [28] .
The reduced “visibility” or an expected downturn in activity as proposed by Dreschhoff and Jungner [26] associated with the modern era seems to be confirmed with the advance of the current solar cycle 24, and which has been also predicted by Svalgaard et al. [29] , who “used the sun’s polar magnetic field to predict that cycle 24 would be the weakest for a century”, although other predictive models deviated by predicting actually a very strong cycle in 2012 [30] . A significant downturn or reduction in solar activity is clearly being recognized as the data for the current cycle remain very low (Solar Cycle Prediction: NASA/Marshall Solar Physics; The Next Grand Minimum posted by Russ Steele [31] .
In summary: the question of understanding how magnetic energy is linked to the interior we put forward the conjecture that synchronous oscillations in the core may be a controlling factor in global oscillation, in other words harmonic progression is governing global oscillations which is also reflected in longer term behavior as expressed in Figure 1 and Figure 4. This concept may also include the presence of stronger versus weaker pressure waves or activity cycles totally in association with the variation in the fusion burning process of 1H and 3He [1] .
Furthermore, the pressure waves as they permeate or traverse the solar body will provide the probability for the conditions of 2D zones to form involving any number of relativistic 2D hydrogen. Near or at the surface such conditions are expected to be detectable through the release of energetic 0.5 MeV gamma radiation. In an environment where strong or steep pressure variation may occur, such as in large, violent thunderclouds/ lightening-storms, the situation may present itself to similar conditions for short term 2D relativistic hydrogen to form with subsequent Chern-Simons ground state photon release, i.e. gamma radiation. We suggest that this process does not require speculating about the formation of a rather large “cloud” of anti-matter or positrons (electron/positron annihilation) to explain the 511 KeV gamma radiation measured by a team flying through a powerful storm as recently reported in Nature [32] . Furthermore, the 2D relativistic hydrogen and subsequent release of the ground state binding energy of 0.5 MeV would at the same time be accompanied by lower energy gammas as transitions between intermediate energy levels in the 2D hydrogen would be expected to occur, again an additional fact which remains unsatisfactorily explained in [32] .
More detailed analytical work is anticipated in future work.