Real Time Systems with Nonpreemptive Priorities and Ample Maintenance Facilities ()
1. Introduction
Real time systems (RTS) are imbedded in most modern technological structures, such as production control systems, robotic and telecommunications systems, radars, self-guided missiles, reconnaissance, aircraft and space stations, etc. These systems are widely used for the monitoring and control of physical processes.
The sustained demands of the environments in which RTS operate pose relatively rigid requirements (usually stated as time constraints) on their performance.
In RTS, a calculation that uses temporally invalid data or an action performed too early/late may be useless, and sometimes harmful―even if such a calculation or action is functionally correct. These systems are often associated with applications, in which human lives or expensive machinery may be at stake.
There exists a rich literature covering RTS and different scientific communities are treating various problems in this area. We will site only a small portion of it.
Liu and Layland in their famous work [1] presented analytic combinatorial analysis for multiprogram scheduling on a single processor. They suggested two preemptive priority driven algorithms.
Dhall and Liu [2] treated the problem of specifying an order in which the requests made by a set of periodic real-time jobs are to be executed by a multiprocessor computing system, with the goal of meeting all the deadlines with a minimum number of processors. Xio et al. in [3] presented a general cost model and an optimal solution algorithm achieving required performance objective (reliability and availability) for redundant RTS.
Several authors treated real-time Flexible Manufacturing Systems (FMS). Tawegoum et al. [4] introduced management functions in real-time monitoring of FMS. Chakravarty and Balakrishnan [5] presented the procedure for the real-time revision of production and inventory schedules in a capacitated FMS.
Efficient metaheuristic methods, such as Tabu Search (Glover and Laguna [6] ) and Greedy Randomized Adaptive Search Procedure (Feo et al. [7] ) were proposed during the last two decades of the previous century. A comprehensive survey on real-time decision problems in OR perspective is given in (Seguin et al. [8] ). Good survey on applications of Artificial Intelligence to RTS is given in (Strosnider and Paul [9] ).
We will focus on RTS with a zero deadline for the beginning of job processing. Queueing of jobs in such systems is impossible, since jobs are executed immediately upon arrival, conditional on system availability.
That part of the job which is not processed immediately is lost forever and cannot be served later.
The following works treated this kind of RTS. Kreimer and Mehrez ( [10] and [11] ) showed that the non-mix policy of never relieving an operative server maximizes the availability of a single channel RTS involving preventive maintenance and working in general regime with any arrival pattern under consideration and constant service and maintenance times. Kreimer and Mehrez [12] and Kreimer [13] treated muliserver and multichannel (with identical servers and channels) RTS (with unrestricted and restricted number of maintenance facilities respectively), working under maximum load regime (worst case) as finite source queues (Gross and Harris, [14] ). Kreimer [15] applied the two dimensional birth and death processes in worst case analysis of a multiserver RTS (with ample and limited maintenance facilities respectively) with two different channels, when both service and maintenance times were exponentially distributed. Ianovsky and Kreimer [16] obtained optimal assignment/ routing probabilities to maximize the availability of RTS with limited maintenance facilities, for large number of servers and two different channels. Kreimer [17] obtained the steady state probabilities for RTS with arbitrary number of different channels operating under a maximum load regime. Kreimer [18] considered multiserver and multichannel RTS working in general regime. Shimshi and Kreimer [19] and Kreimer [20] studied single- channel RTS with two different kinds of activities. In [21] we computed analytically (for exponentially distributed service times) and via Cross Entropy [22] - [24] simulation approach (for generally distributed service times) optimal routing probabilities for RTS with ample maintenance facilities. Bassan and Kreimer [25] treated RTS with preemptive priorities.
The work presented here is a generalization of results obtained by Shimshi and Kreimer [19] and Kreimer [20] for RTS with single channel and two kinds of activities. It deals with multiserver RTS, providing the service to the requests of real-time jobs arriving via several channels. Servers are identical, but may be maintained/pro- grammed for several (two or more) kinds of activities. We provide balance equations describing two models (with and without nonpreemptive priorities) operating under a maximum load regime and show how to compute various performance measures, when both operation and maintenance times are exponentially distributed.
The paper is organized as follows: In Section 2, the description of the model is presented. Section 3 provides balance equations for RTS with nonpreemptive priorities. Section 4 provides balance equations for RTS without priorities. Section 5 is devoted to computation of various performance characteristics. Finally, Section 6 contains conclusions.
2. Description of the Model
The most important characteristics of RTS with a zero deadline for the beginning of job processing are summarized in Kreimer and Mehrez [24] as follows:
1) Jobs/data acquisition and execution are as fast as the data arrival rate.
2) Jobs are executed immediately upon arrival, conditional on system availability. Between jobs arrival and their execution, delays are negligible.
3) That part of the job which is not executed in real time is lost forever. Storage of non-completed jobs or their parts is impossible. Thus, queues of jobs do not exist in such an RTS.
Nevertheless, some important elements of queueing theory can be successfully applied in analysis of these RTS.
We consider a multiserver multichannel RTS consisting of N identical servers (e.g. unmanned aerial vehicles- UAV, machine controllers, overhearing devices, medical monitoring devices, etc.) that provide service for the requests of real time jobs, arriving via r identical channels (e.g. surveillance regions, assembly lines, communication channels, hospital patients, etc.).
Each server can serve different channels, but not simultaneously. There is exactly one request in each channel at any instant (there are no additional job arrivals, while the channel is busy), and therefore one server at most is used (with others being on stand-by or in maintenance or providing the service to another channel) to process the job of this channel at any given time. Thus, the total number of jobs in the system is r (is equal to a number of channels). Different parts of the same job can be served by different servers. Any part of the job that is not processed immediately is lost.
It is assumed that there are ample identical maintenance teams available to repair (with repair times 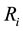 being independent identically distributed random variables―i.i.d.r.v.) all N servers simultaneously, if needed. Thus, each broken server enters maintenance facilities without delay. A fixed server may be of one of m kinds (e.g. of activity or quality) with probabilities
being independent identically distributed random variables―i.i.d.r.v.) all N servers simultaneously, if needed. Thus, each broken server enters maintenance facilities without delay. A fixed server may be of one of m kinds (e.g. of activity or quality) with probabilities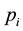 ,
, 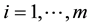 respectively. These probabilities can be used sometimes as control parameters. Only after the maintenance is completed, the type of fixed server can be determined. The fixed server of i-th type is operative for a period of time
respectively. These probabilities can be used sometimes as control parameters. Only after the maintenance is completed, the type of fixed server can be determined. The fixed server of i-th type is operative for a period of time 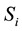 before requiring
before requiring 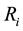 hours of repair. Both
hours of repair. Both 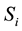 and
and  are independent exponentially distributed random values with parameters
are independent exponentially distributed random values with parameters 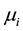
 and
and  respectively. The duration
respectively. The duration 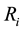 of maintenance does not depend on the server’s type (neither before nor after the maintenance). After maintenance is completed, the fixed server will either be on stand-by or providing service to one of channels.
of maintenance does not depend on the server’s type (neither before nor after the maintenance). After maintenance is completed, the fixed server will either be on stand-by or providing service to one of channels.
The system works under a maximum load (worst case) of nonstop data arrival, which is equivalent to the case of a unique job of infinite duration in each one of r channels. This kind of operation is typical in high performance data acquisition and control systems. Decisions based on the nonstop data flow arriving via all r channels must be made extremely fast―in real time. If, during some period of time of length T, there is no available server to serve one of the channels, it means that the part of the job of length T is lost forever.
Our purpose is to provide balance equations for steady-state probabilities of this system, its availability and other performance characteristics. We will consider two policies/models: 1) nonpreemptive priority; 2) random choice of the fixed server.
3. Model with Nonpreemptive Priority
First we will provide the list of various terms, which are used in our equations.
3.1. Equations
We suppose that servers of first activity type have the highest priority, servers of the second activity type are after them, and so on, finally, servers of the m-th activity type have the lowest priority (Figure 1). Operating server is not interrupted, independently of its priority. When the operating server must be repaired, the fixed server with highest priority takes its place.
We denote  the state of the system, where
the state of the system, where 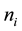
 is the total number of fixed servers of i-th activity type and
is the total number of fixed servers of i-th activity type and 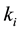
 is the number of operating (providing service) fixed servers of i-th activity type respectively, and
is the number of operating (providing service) fixed servers of i-th activity type respectively, and ![]() the corresponding steady state probability. It is clear that
the corresponding steady state probability. It is clear that![]() .
.
Theorem 1. Steady state probabilities for the model with nonpreemptive priorities can be found from the fol- lowing system of balance equations:
![]() (1)
(1)
where ![]() is any feasible state of the system,
is any feasible state of the system,![]() .
.
And
![]() (2)
(2)
where ![]() is the set of all feasible states of the system.
is the set of all feasible states of the system.
Proof:
1) First we consider the case![]() . Then it is clear that
. Then it is clear that![]() ,
, ![]() , i.e. all fixed servers must be operative and priorities do not work in this case (each server coming from maintenance immediately start to work independently of its priority class). We have therefore [26]
, i.e. all fixed servers must be operative and priorities do not work in this case (each server coming from maintenance immediately start to work independently of its priority class). We have therefore [26]
![]() (3)
(3)
for the state![]() , i.e.
, i.e.![]() ,
,![]() ;
;
![]() (4)
(4)
for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
![]() (5)
(5)
for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
![]() (6)
(6)
for the states![]() ,
, ![]() ,
,![]() ;
;
![]() (7)
(7)
for the states![]() ,
, ![]() ,
,![]() ;
;
Now Equation (1) follows from Equations (3)-(7).
2) Next, we consider the case![]() . Then we have:
. Then we have:
Equation (3) again for the state![]() , i.e.
, i.e.![]() ,
,![]() ;
;
Equation (4) for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
Equation (6) for the states![]() ,
, ![]() ,
,![]() ;
;
![]() (8)
(8)
for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
![]() (9)
(9)
for the states![]() ,
, ![]() ,
,![]() ;
;
![]() (10)
(10)
for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
![]() (11)
(11)
for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
![]() (12)
(12)
for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
![]() (13)
(13)
for the states![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
![]() (14)
(14)
for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
![]() (15)
(15)
for the states![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
Now, Equation (1) follows from Equations (3), (4), (6), (8)-(15).
Q.E.D.
4. Model without Priorities
We suppose that when the operating server must go to maintenance, the server which takes its place is chosen among the fixed servers in a random way (Figure 2). Namely, if there are ![]() fixed servers of the i-th activity type
fixed servers of the i-th activity type ![]() on stand-by, then it is chosen for operation with probability
on stand-by, then it is chosen for operation with probability![]() . Denoting the state of the system
. Denoting the state of the system ![]() and the corresponding steady state probability
and the corresponding steady state probability ![]() as in previous Section, we obtain
as in previous Section, we obtain
Theorem 2. Steady state probabilities for the model without priorities can be found from the following system of balance equations:
![]() (16)
(16)
where ![]() is any feasible state of the system,
is any feasible state of the system,![]() .
.
And
![]() (17)
(17)
where ![]() is the set of all feasible states of the system.
is the set of all feasible states of the system.
Proof:
1) First, we consider the case![]() . Then, it is clear that there are no fixed servers on stand-by, i.e. all fixed servers are operative. Each server coming back from maintenance immediately starts to work. We, therefore, have the same situation (and Equations (3)-(7)) as in Theorem 1 of the previous section.
. Then, it is clear that there are no fixed servers on stand-by, i.e. all fixed servers are operative. Each server coming back from maintenance immediately starts to work. We, therefore, have the same situation (and Equations (3)-(7)) as in Theorem 1 of the previous section.
2) Next, we consider the case![]() . Then equations of previous Section do not change for the following types of states:
. Then equations of previous Section do not change for the following types of states:
Equation (3) for the state![]() , i.e.
, i.e.![]() ,
,![]() ;
;
Equation (4) for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
Equation (6) for the states![]() ,
, ![]() ,
,![]() ;
;
Equation (8) for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
Equation (9) for the states![]() ,
, ![]() ,
,![]() ;
;
Equation (14) for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
And Equation (15) for the states![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
For the states below, we will have following new equations:
![]() (18)
(18)
for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
![]() (19)
(19)
for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
![]() (20)
(20)
for the states![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
![]() (21)
(21)
for the states![]() ,
, ![]() ,
, ![]() ,
,![]() ;
;
Now, Equations (16) follows from Equations (3), (4), (6), (8), (9), (14), (15), (18)-(21).
Q.E.D.
5. Performance Characteristics
In this section, we shall show how to compute some useful performance characteristics of the RTS under consideration.
Each server can be in one of following positions:
a) Busy (operating);
b) Out of order (in maintenance);
c) On stand-by;
Each channel can be in one of two positions:
a) In service;
b) Out of service.
Keeping in mind that, the state of the system is represented by the vector![]() , where
, where ![]()
![]() is the total number of fixed servers of i-th activity type and
is the total number of fixed servers of i-th activity type and ![]()
![]() is the number of operating fixed servers of i-th activity type, we can represent the number of servers and channels in different positions in terms of
is the number of operating fixed servers of i-th activity type, we can represent the number of servers and channels in different positions in terms of ![]() and
and![]() , namely:
, namely:
Number of fixed servers is![]() ;
;
Number of operating fixed servers (the number of channels in service) is![]() ;
;
Number of fixed servers of i-th activity type being on stand-by is![]() ;
;
Number of all fixed servers being on stand-by is![]() ;
;
Number of broken servers is![]() ;
;
Number of channels out of service is![]() ;
;
Now we can obtain corresponding average values, using steady state probabilities, namely:
![]() ―average number of fixed servers of i-th activity type
―average number of fixed servers of i-th activity type![]() ;
;
![]() ―average number of all fixed servers;
―average number of all fixed servers;
![]() ―average number of broken servers (also the average number of servers in maintenance);
―average number of broken servers (also the average number of servers in maintenance);
![]() ―average number of operating servers of i-th activity type
―average number of operating servers of i-th activity type![]() ;
;
![]() ―average number of all operating servers (as well as the average number of channels in service);
―average number of all operating servers (as well as the average number of channels in service);
![]() ―average number of non-executed real-time jobs;
―average number of non-executed real-time jobs;
![]() ―average number of i-th type fixed servers on stand-by
―average number of i-th type fixed servers on stand-by![]() ;
;
![]() ―average number of all fixed servers on stand-by;
―average number of all fixed servers on stand-by;
![]() ―average rate of servers arriving from maintenance;
―average rate of servers arriving from maintenance;
![]() ―average rate of i-th type servers arriving from maintenance
―average rate of i-th type servers arriving from maintenance![]() ;
;
![]() ―average time spent on stand-by by the i-th type server
―average time spent on stand-by by the i-th type server ![]() -Little Theorem;
-Little Theorem;
![]() ―average time of the i-th type server being fixed
―average time of the i-th type server being fixed ![]() -Little Theorem.
-Little Theorem.
The use of RTS relies on the principle of availability, which can be given in our case by the following formula![]() .
.
Another important performance measure is the average cost of system operation during time unit. Denote ![]()
![]() the cost of time unit activity of the i-th type server, and D the penalty paid for the time unit during which one of channels was not served. Then the average cost is defined as follows
the cost of time unit activity of the i-th type server, and D the penalty paid for the time unit during which one of channels was not served. Then the average cost is defined as follows
![]()
6. Conclusions
In this paper, we provided equations for steady-state probabilities, as well as formulas for availability, average cost function and other performance characteristics of multiserver and multichannel RTS with different activity types and ample maintenance facilities. We have examined models with nonpreemptive priorities and without them. Practitioners and researchers can submit their parameters in equations for steady state probabilities and performance characteristics and to make their choice between two models in order to solve real life problems. Further research should address following problems:
![]() RTS with preemptive priorities;
RTS with preemptive priorities;
![]() RTS in which each server needs more than one kind of maintenance;
RTS in which each server needs more than one kind of maintenance;
![]() Optimization of RTS involving costs and penalties;
Optimization of RTS involving costs and penalties;
![]() Multilevel RTS;
Multilevel RTS;
![]() RTS with shortage of maintenance teams.
RTS with shortage of maintenance teams.
The use of queueing theory methodology will have significant benefits in analysis of these systems.
Notations
N number of servers
r number of channels
m number of server’s activity or quality kinds/types
![]() i = th type server’s operation/service time
i = th type server’s operation/service time ![]()
![]() i = th type server’s operation/service time (exp) parameter
i = th type server’s operation/service time (exp) parameter ![]()
![]() intenance time
intenance time
![]() server’s maintenance time parameter (exp)
server’s maintenance time parameter (exp)
![]() routing probabilities to i-th kind
routing probabilities to i-th kind ![]()
![]() total number of fixed servers of i-th activity type
total number of fixed servers of i-th activity type ![]()
![]() number of operating fixed servers of i-th activity type
number of operating fixed servers of i-th activity type ![]()
![]() number of fixed servers of i-th activity type
number of fixed servers of i-th activity type ![]() on stand-by
on stand-by
![]() the state of the system
the state of the system
![]() the corresponding steady state probability
the corresponding steady state probability
![]() the cost of time unit activity of the i-th type server
the cost of time unit activity of the i-th type server ![]()
D penalty cost for the time unit during which one of channels was not served
Av system availability
TC an average total cost of system operation per time unit