Auto-Bäcklund Transformation and Extended Tanh-Function Methods to Solve the Time-Dependent Coefficients Calogero-Degasperis Equation ()
1. Introduction
Recently, investigation of exact solutions for nonlinear partial differential equations (NPDEs) with variable coefficients plays an important role in modern nonlinear science because NPDEs with variable coefficients reflect the real thing even more than those with constant.
One of the most important NPDEs is the time-dependent coefficients Calogero-Degasperis (VCCD) equation [1]
(1)
where 
and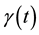 
are arbitrary functions. The VCCD equation describes the (2 + 1)-dimensional interaction of the Riemann wave propagating along the y-axis with a long wave along the x-axis. Many exact solutions have been found for Equation (1) by using symmetry method [1] . Equation (1) with 
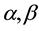and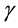 
as constants was first constructed by Bogoyavlenskii and Schiff in different ways [2] -[4] and called the Calogero- Bogoyavlenskii-Schiff (CBS) equation. Bogoyavlenskii used the modified Lax formalism, whereas Schiff derived the same equation by reducing the self-dual Yang-Mills equation. The CBS equation has been solved by using Hirota’s bilinear method [5] and symmetry method [6] .
The objective of this paper is to apply the auto-Bäcklund transformation method and the extended tanh- function method on the VCCD equation, to find more general new solitonic and periodic exact solutions.
2. Auto-Bäcklund Transformation
We can obtain Auto-Bäcklund transformation by using HB method [7] -[10] as follows.
Step 1: We consider the exact solution of (1) in the form
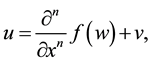(2)
where 
and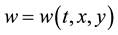 
are undetermined functions, 
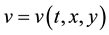is a solution of (1).
According to the HB method n can be determined by balancing the linear term of the highest order derivative and the highest nonlinear term of u in (1).
Therefore,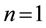 
and
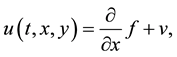(3)
Substituting (3) into (1), we get
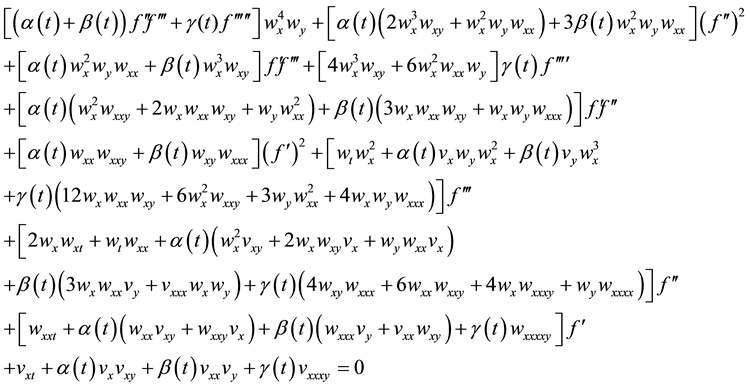(4)
Step 2: To make (4) as a linear equation in f we assume that,
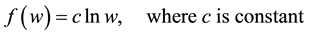(5)
So that, we have the following relations
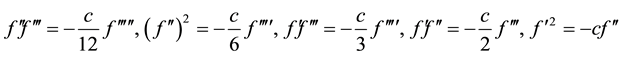(6)
Substitute from relations (6) into (4) and equating the linear coefficients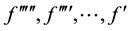 
by zero, the fol- lowing partial differential system is obtained
![]()
![]()
![]()
![]()
![]()
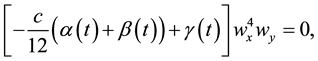
(7)
Step 3: To solve the previous system, assume that
![]()
(8)
where ![]()
are arbitrary constants and ![]()
is an arbitrary function of t. Then, we obtain the following relations
![]()
(9)
![]()
(10)
By substitution from (8-10) into (3) using (5), we obtain the following one-soliton solution for the VCCD equation under condition (9)
![]()
(11)
By using the following two useful formulas [11]
![]()
(12)
![]()
(13)
We obtain the following kink-type soliton and periodic solutions respectively
![]()
(14)
![]()
(15)
Analogously, we assume that ![]()
and ![]()
in (11), where ![]()
and ![]()
are real constants. So the fol- lowing new periodic solutions for the VCCD equation are obtained
![]()
(16)
![]()
(17)
3. The Extended Tanh-Function Method
In this section, we are going to find more new exact solutions for the VCCD equation using direct integration and extended tanh-function method [12] [13] . Assume that
![]()
(18)
where ![]()
and ![]()
are arbitrary constants and ![]()
is an arbitrary function of t.
By substitution in (1), we have
![]()
(19)
To make the previous Equation (19) be an ordinary differential equation, we have found
![]()
(20)
![]()
(21)
Therefore, (19) becomes
![]()
(22)
By Integrating (22) twice, we get
![]()
(23)
where ![]()
and ![]()
are integration constants. Assume that![]()
, then (23) becomes
![]()
(24)
Now, we apply the extended tanh function method used in [14] to obtain exact travelling wave solutions of Equation (24). Let us assume that Equation (24) has a solution in the form
![]()
(25)
where ![]()
is a solution of the following Riccati equation
![]()
(26)
This Riccati equation has the following solutions
![]()
![]()
![]()
![]()
![]()
(27)
Substitute from (25) into Equation (24) and balance the term ![]()
with the greatest nonlinear term![]()
, we get that
![]()
(28)
Therefore,
![]()
(29)
where ![]()
and ![]()
are constants to be determined. Then, by substitution from (29) and (26) in (24), and equating the coefficients of ![]()
and all its powers with zero, we obtain an algebraic system by solving it with mathematica program many values of ![]()
and ![]()
are obtained. We have chosen one of them for simplicity
![]()
(30)
By substitution from (30) and (27) in (29), we have got the following exact solutions for Equation (24)
![]()
![]()
(31)
and ![]()
for Equations (31). By back substitution from (31) into (18) using
the relation ![]()
and (20-21), we have got the following new exact solutions for the VCCD equation.
![]()
(32)
![]()
(33)
where ![]()
![]()
(34)
![]()
(35)
where ![]()
The following part of this section is devoted to analyzing the influences of the variable coefficients on the solitonic propagation. From the expression of![]()
, we can get the characteristic line of the soliton solution [15] -[17] as
![]()
(36)
from the previous equation, we have found that there are three arbitrary constants ![]()
and c so that it is important to control the solitonic velocity in the profile at ![]()
(or y is constant) by choosing appropriate parameters. Correspondingly, the velocity v of the solitary wave along the x-axis can be expressed as
![]()
(37)
Therefore, the propagation direction of the soliton is decided by the sign of v and the solitonic velocity depend on the variables ![]()
and ![]()
and the same can be done for the kink-soliton solution ![]()
The previous figures indicate that how the variable coefficients ![]()
affect the evolution of the soliton in Figures 1-6. In Figure 2, Figure 3, Figure 5 and Figure 6, we can see that the solitonic propagation
![]()
Figure 1. The soliton solution u1 with α(t) = β(t) = 1 and k = r = c = C = υ0 = 1.
![]()
Figure 2. The soliton solution u1 with α(t) = β(t) = t and k = r = c = C = υ0 = 1.
![]()
Figure 3. The soliton solution u1 with α(t) = sin(t), β(t) = cos(t) and k = r = c = C = υ0 = 1.
![]()
Figure 4. The kink-soliton solution u6 with α(t) = β(t) = 1 and k2 = r2 = c1 = 1.
trajectory is not a straight line anymore. It exhibits as a parabolic and periodic-type propagation respectively.
![]()
Figure 5. The kink-soliton solution u6 with α(t) = β(t) = t and k2 = r2 = c1 = 1.
![]()
Figure 6. The kink-soliton solution u6 with α(t) = sin(t), β(t) = cos(t) and k2 = r2 = c1 = 1.
4. Conclusions
By using the HB method, we have obtained Auto-Bäcklund transformation and new exact solitary and periodic solutions for the VCCD equation. Also by using a travelling wave transformation, we have reduced the VCCD equation to an ordinary differential equation, by the extended tanh function method we have been able to obtain many other new exact solitary and periodic-type solutions. Some remarks have been found on the obtained so-n lutions
Remark 1: The obtained Bäcklund transformation is more easy and simple in calculations than that obtained in [1] by using Painlevé-test. Additionally, the obtained solutions are also new and more general than solutions in Ref. [1] because all solutions in Ref. [1] depend on only one variable![]()
.
Remark 2: The combination between the two functions ![]()
and ![]()
affects the propagation shape of the solitary wave solution. Moreover, the one-soliton solution ![]()
recovers the single soliton solution obtained by Wazwaz in [5] for the CBS equation.
Remark 3: All solutions obtained in this paper have been satisfied by Mathematica program.