Best Equivariant Estimator of Extreme Quantiles in the Multivariate Lomax Distribution

N. Sanjari Farsipour

Department of Statistics, College of Mathematical Sciences, Alzahra University, Tehran, Iran.

DOI: 10.4236/ojs.2015.54036                

Abstract

The minimum risk equivariant estimator of a quantile of the common marginal distribution in a multivariate Lomax distribution with unknown location and scale parameters under Linex loss function is considered.

Keywords

Best Affine Equivariant Estimator, Quantile Estimation, Lomax (Pareto II) Distributions, Linex Loss Function

1. Introduction

In the analysis of income data, lifetime contexts, and business failure data the univariate Lomax (Pareto II) dis-

tribution with density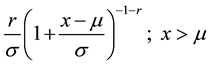, is a useful model [1] . The lifetime of a decreasing failure rate

component may be describe by this distribution. It has been recommended by [2] as a heavy tailed alternative to the exponential distribution. The interested reader can see [3] and [4] for more details.

A multivariate generalization of the Lomax distribution has been proposed by [5] and studied by [6] . It may be obtained as a gamma mixture of independent exponential random variables in the following way. Consider a system of n components. It is then reasonable to suppose that the common operating environment shared by all components induces some kind of correlation among them. If for a given environment, the component lifetimes are independently exponentially distributed with density

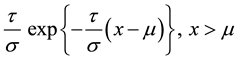, and the changing nature of the environment is accounted by a distribution function

F(.), then the unconditional joint density of 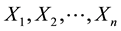is

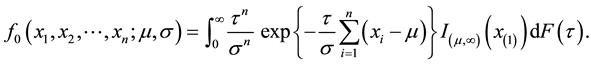(1)

where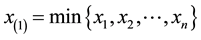. Furthermore, if is a gamma distribution 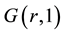with density

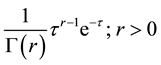, then (1) become

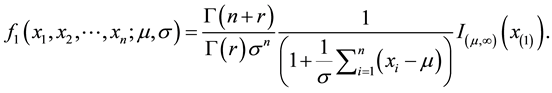(2)

This is called multivariate Lomax with location parameter 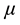and scale parameter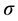. The same distribution is referred to as Mardia’s multivariate Pareto II distribution, see [3] and [7] . If take 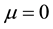and assign a different scale parameter, to each we have

(3)

For more information about the work on this distribution, the reader can see [8] .

2. Best Affine Equivarient Estimator

Let are from a multivariate Lomax distribution with unknown and and known r. We consider the linear function for given. When;, is the 100(1 − p) th quantile of the marginal distribution of. Quantile estimation is of interest in reliability theory and lifetesting. [9] generalized results in [10] to a strictly Convex loss.

In this paper we consider the Linex loss function

(4)

where is the shape parameter, which was introduced by [11] and was extensively used by [12] .

The minimal sufficient statistic in the model (2) is (S, X) where, and. Conditional on, random variable with distribution, S and X are independent with

(5)

So, the density of (S, X) is

(6)

The problem of estimating; under the loss (4) is invariant under the affine group of transformations and the equivariant estimator have the form δ = X + cS where c is a real constant.

Following [13] , we study scale equivariant estimators of the form, where and is

a measurable function. Thus the equivariant estimator is of the form, where. Now, consider the risk of the estimator for estimating when the loss is (4).

(7)

Now, since and and we have

(8)

which is finite if. By the invariant property of the problem we can take and the risk becomes

(9)

Differentiate the risk with respect to c and equating to zero, the minimizing c must satisfies the following equation

(10)

Yielding the best affine equivariant estimator, where

.

3. Improved Estimator

For improving upon, we study scale equivariant estimator. The risk of depends on

through, so without loss of generality one can take and write

(11)

The minimization of leads to the following equation

(12)

let, then the conditional density of S given is proportional to

(13)

Consider now and fix, then setting

(14)

From (12) we compute the following expectations as follows

and

where. Hence (12) becomes

(15)

any satisfying (15) minimizes, for and. Now, let

and fix again, then,.

So we have

and

and hence (7) becomes

(16)

any satisfying (16) minimizes for and [14] . Now for deriving an improved equivariant estimator upon this we must find a bound for c in formula (15) and (16). As we can not derive c from Equations (15) and (16) explicitely, this would not be achieved.

Acknowledgements

The grant of Alzahra University is appreciated.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Lomax, K. (1954) Business Failures: Another Example of the Analysis of Failure Data. Journal of the American Statistical Association, 94, 847-852. http://dx.doi.org/10.1080/01621459.1954.10501239
[2]	Bryson, M. (1974) Heavy-Tailed Distributions: Properties and Tests. Technometrics, 16, 61-68. http://dx.doi.org/10.1080/00401706.1974.10489150
[3]	Arnold, B. (1983) Pareto Distribution. International Cooperative Publishing House, Silver Spring Maryland.
[4]	Johnson, N., Kotz, S. and Balakrishnan, N. (1994) Continous Univariate Distributions. Vol. 1, 2nd Edition, Wiley & Sons, New York.
[5]	Lindley, D. and Singpurwalla, N (1986) Multivariate Distributions for the Life Lengths of Components of a System Sharing a Common Environment. Journal of Applied Probability, 23, 418-431. http://dx.doi.org/10.2307/3214184
[6]	Nayak, Tk. (1987) Multivariate Lomax Distribution: Properties and Usefulness in Reliability Theory. Journal of Applied Probability, 24, 170-177. http://dx.doi.org/10.2307/3214068
[7]	Kotz, S., Balakrishnan, N. and Johnson, N.L. (2000) Continuous Multivariate Distributions, Vol. 1, Models and Applications, 2nd Edition, Wiley & Sons, New York.
[8]	Petropoulos, C. and Kourouklis, S. (2004) Improved Estimation of Extreme Quantiles in the Multivariate Lomax (Pareto II) Distribution. Metrika, 60, 15-24. http://dx.doi.org/10.1007/s001840300293
[9]	Petropoulos, C. and Kourouklis, S. (2001) Estimation of an Exponential Quantile under a General Loss and an Alternative Estimator under Quadratic Loss. Annals of the Institute of Statistical Mathematics, 53, 746-759. http://dx.doi.org/10.1023/A:1014648819462
[10]	Rukhin A. and Strawderman, W. (1982) Estimating a Quantile of an Exponential Distribution. Journal of the American Statistical Association, 77, 159-162. http://dx.doi.org/10.1080/01621459.1982.10477780
[11]	Varian, H.R. (1975) A Bayesian Approach to Real Estat Assessment. In: Fienberg, S.E. and Zellner, A., Eds., Studies in Bayesian Econometric and Statistics: In Honor of Leonard J. Savage, North Holland, Amesterdam, 195-208.
[12]	Zellner, A. (1986) Bayesian Estimation and Prediction Using Asymmetric Loss Function. Journal of American Statistical Association, 81, 446-451. http://dx.doi.org/10.1080/01621459.1986.10478289
[13]	Stein, C. (1964) Inadmissibility of the Usual Estimator for the Variance of a Normal Distribution with Unknown Mean. Annals of the Institute of Statistical Mathematics, 16, 155-160. http://dx.doi.org/10.1007/BF02868569
[14]	Brewster, J.F. and Zidek, J.V. (1974) Improving on Equivariant Estimators. Annals of Statistics, 2, 21-38. http://dx.doi.org/10.1214/aos/1176342610