Optimization of Threshold for Energy Based Spectrum Sensing Using Differential Evolution ()
1. Introduction
The increasing demand for mobility and portability in communication equipment has made wireless communication an indispensable field of research. The focus today is to construct wireless networks or nodes that can dynamically reconfigure their transmission and reception parameters. Spectrum sensing and its utilization are thus ubiquitous. This concept is called a cognitive radio and the first main function of such a system is to detect the unused spectrum and transmit in it without interference to primary users.
Newer wireless technologies crop up everyday providing better service to the users. The 3G or third generation of wireless networks are only being rolled out in most countries and research is already on to take communication to the next level with 4G or Long Term Evolution (LTE) [2]. All of these technologies focus on providing new features to the users, such as video conferencing, high speed internet etc. with a better quality of service.
Simultaneously, newer techniques are also being developed for making better utilization of the wireless resources available. One such technology is cognitive radio [3]. A wireless network consisting of nodes that are capable of dynamically changing their transmission and reception parameters is called a cognitive radio. One of the main resources that the cognitive radio aims at optimizing is the frequency spectrum. It does this by allowing the secondary users to detect and utilize portions of the licensed spectrum that are not being used by the primary user. The process of detecting unused frequencies or spectral holes is called spectrum sensing [1]. Methods of sensing spectral holes include energy based detection, matched filter based detection, cyclostationary methods etc. In this paper, we propose a method of energy based spectrum sensing using differential evolution to optimize the threshold used for detection.
The organization of the paper is as follows. In section II, we explain in detail the sensing problem for threshold based detection of spectral holes. In section III, we present an analysis of the optimization techniques that can be used for this process and explain why we choose differential evolution. Section IV is dedicated to our proposed method of threshold based spectrum sensing using differential evolution. In Section V, we present the results obtained and compare the performance of differential evolution with that of genetic algorithms. Section VI concludes the paper, where we restate our major observations and future work.
2. The Sensing Problem
The sensing problem under consideration here is same as the one used in [4]. The wide band spectrum is divided in to K narrow sub-bands and each sub-band can be in two possible states H0 and H1.
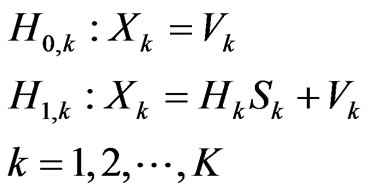
H0 represents a spectral hole and H1 represents an occupied channel. Vk is the Gaussian noise with power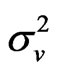 , Hk is the channel impulse response in the frequency domain and Sk is the frequency spectrum of the signal.
, Hk is the channel impulse response in the frequency domain and Sk is the frequency spectrum of the signal.
In order to find out whether a channel is occupied or free, we use the following energy detector.
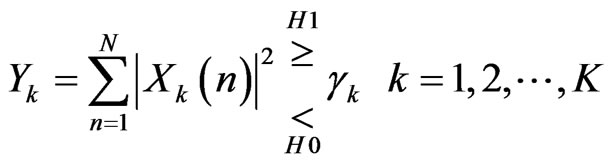 (1)
(1)
where γk is the threshold for the kth sub-band and N is the number of measurements made for each sub-band. When N is large enough, the random variables of the energy detector Yk can be considered to follow a normal distribution, that is Yk~N (µ0,k,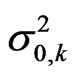 ) for the state H0,k and Yk~N (µ1,k,
) for the state H0,k and Yk~N (µ1,k,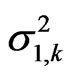 ) for the state H1,k. The sensing performance can be quantified based on the probability of identifying a spectral hole, as in (2), and the probability of identifying an occupied channel as a hole, as in (3).
) for the state H1,k. The sensing performance can be quantified based on the probability of identifying a spectral hole, as in (2), and the probability of identifying an occupied channel as a hole, as in (3).
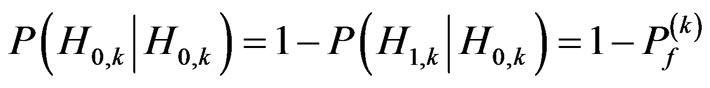 (2)
(2)
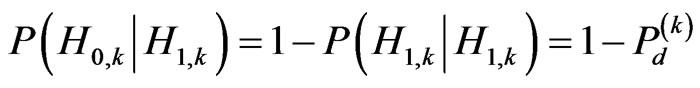 (3)
(3)
In (2) and (3), Pf and Pd are the probability of false alarm and probability of detection of a transmission respectively. Here 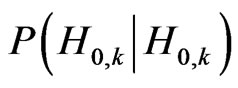 represents the probability of correctly detecting a spectral hole as a spectral hole, and not the Bayesian probability of occurrence of one event given another has occurred. This representation holds for similar probability terms encountered in (2), (3), (4) and (5).
represents the probability of correctly detecting a spectral hole as a spectral hole, and not the Bayesian probability of occurrence of one event given another has occurred. This representation holds for similar probability terms encountered in (2), (3), (4) and (5).
The consideration that the energy detector specified in (1) will follow a normal distribution on taking a large number of measurements N allows us to compute the values of Pf and Pd from the cdf of the normal distribution as shown below in (4) and (5).
 (4)
(4)
 (5)
(5)
The γk values should be optimized such that the channel interference is minimum and the throughput achieved by the secondary user is maximum. For this purpose, we use the throughput achievable through each of the k channels, and the interference cost that has to be incurred on transmitting through the channels. The objective functions for the optimization can then be formulated, as in (6) and (7), using these values and the probability of identifying a spectral hole and the probability of missed detection.
 (6)
(6)
 (7)
(7)
where Pd (γ) and Pf (γ) are k dimensional vectors with each element representing the probability of detection and probability of false alarm correspondingly in the respective sub-band; r is the vector containing the throughputs attainable through each channel and c is the vector containing interference costs incurred on transmitting through each of the channel.
3. Optimization Techniques and Differential Evolution
The non-convex nature of the objective function posed above limits us from using the conventional optimization methods like convex maximization. Hence, we considered optimizing using direct search algorithms such as genetic algorithm [5], particle swarm optimization [6] and differential evolution [7]. These optimization techniques are useful in the sense that they do not require the objective or cost functions to be differentiable or linear. The knowledge of an objective function that has to be minimized is alone sufficient for these techniques. Moreover, they also have sufficient safeguards to prevent the algorithm from being stuck at a local minimum. An example of this is the mutation step of genetic algorithms [5]. The requirements of these algorithms is that they should have good convergence properties and should not involve too many or complex control variables.
Existing methods for threshold optimization in spectrum sensing use genetic algorithms [4]. Differential evolution is a direct search technique that iteratively improves the fitness of the candidate solutions. It tries to optimize the requirements by using its own formulae for mutation and crossover to create new candidate solutions. The fitness of these new candidates decides whether to replace the existing population members or not.
The working of the differential evolution algorithm is simple.
1) It has a population of candidate solutions that are sometimes called agents.
2) Positions of existing agents are combined using a mathematical formula to move the agents around the search space.
3) If there is an improvement from the old position to the new position of an agent, then it is accepted as a member of the population, else it is discarded.
4) This process is iteratively repeated to arrive at the optimal solution.
It has been shown through extensive experimental testing that the convergence properties of differential evolution are better than that of genetic algorithms [7]. Specifically, differentially evolution has been found to converge faster than genetic algorithms in most cases.
This has prompted us to utilize differential evolution for optimizing the threshold values involved in energy based spectrum sensing.
4. Threshold Optimizsation Using Differential Evolution
We apply the differential evolution optimization technique to the sensing problem under consideration here, with (6) and (7) as the objective functions. A set of N threshold vectors, each of the form
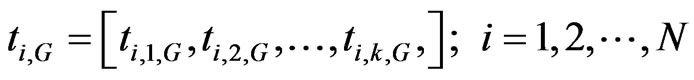 .
.
with random values, is taken as the initial population set. G denotes the generation number. This set represents the potential candidates for optimization and is the first generation of the differential evolution scheme discussed below [7].
The best threshold set in each generation is the one which gives optimal values for throughput (6) and interference (7).
The next generation of vectors is generated as follows. For every vector, ti,G (target vector), the following three steps are performed.
1) Mutation: Three mutually distinct vectors tr1,G, tr2,G, tr3,G are taken such that  . A mutant vector/donor vector is generated according to
. A mutant vector/donor vector is generated according to
 (8)
(8)
where F 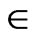 [0, 2] is a constant which controls the magnitude of the differential variation.
[0, 2] is a constant which controls the magnitude of the differential variation.
2) Crossover: The diversity of the vector set is increased by developing a trial vector as
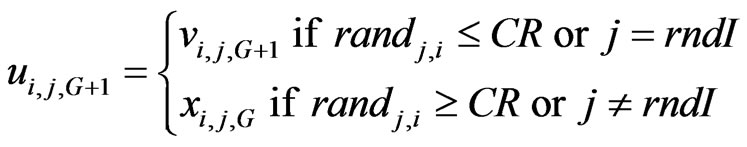 (9)
(9)
 ;
;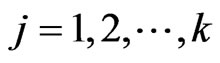 ;
; 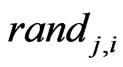 U[0, 1]; rndI is a random integer from [
U[0, 1]; rndI is a random integer from [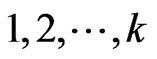 ]; rndI ensures that at least one element from vi, G + 1 is incorporated into ui, G + 1.
]; rndI ensures that at least one element from vi, G + 1 is incorporated into ui, G + 1.
CR is the crossover constant [0, 1] and its value is chosen by the user. A higher value of CR causes more elements from the mutant vector vi, G + 1 to get incorporated in the trial vector ui, G + 1. It has been shown in [7] that a higher value (such as 0.9 or 1) of CR is a good choice and can lead to faster convergence. Hence the value of CR has been chosen as .95.
3) Selection: The trial vector ui, G + 1 is compared with the target vector vi, G + 1 and the one that gives the best values for R and I is passed on to the next generation as ti, G + 1.
The algorithm is continued till the optimum threshold vector is found.
5. Results and Observations
The optimization of the threshold values was done using both GA and DE. In order to compare the performance of the two methods, we use the number of function evaluations required as a parameter. Further, we also plot the interference vs. throughput curves of the final population with interference as the independent variable, for both DE and GA.
Simulations were done using MATLAB and the values of r, c and H are the same as used in [4].
5.1. Function Evaluations
The number of function evaluations that an optimization algorithm requires to converge to the optimum value is an important parameter for measuring the performance. The lower the number of function evaluations required, lesser the computational load and faster the convergence.
On optimizing the threshold using both GA and DE, we found that the number of function evaluations required by DE is far less than that of GA. Figure 1 shows the final pareto front after optimization was done using GA. It also shows the number of function evaluations required for convergence. Figure 2 shows the final pareto
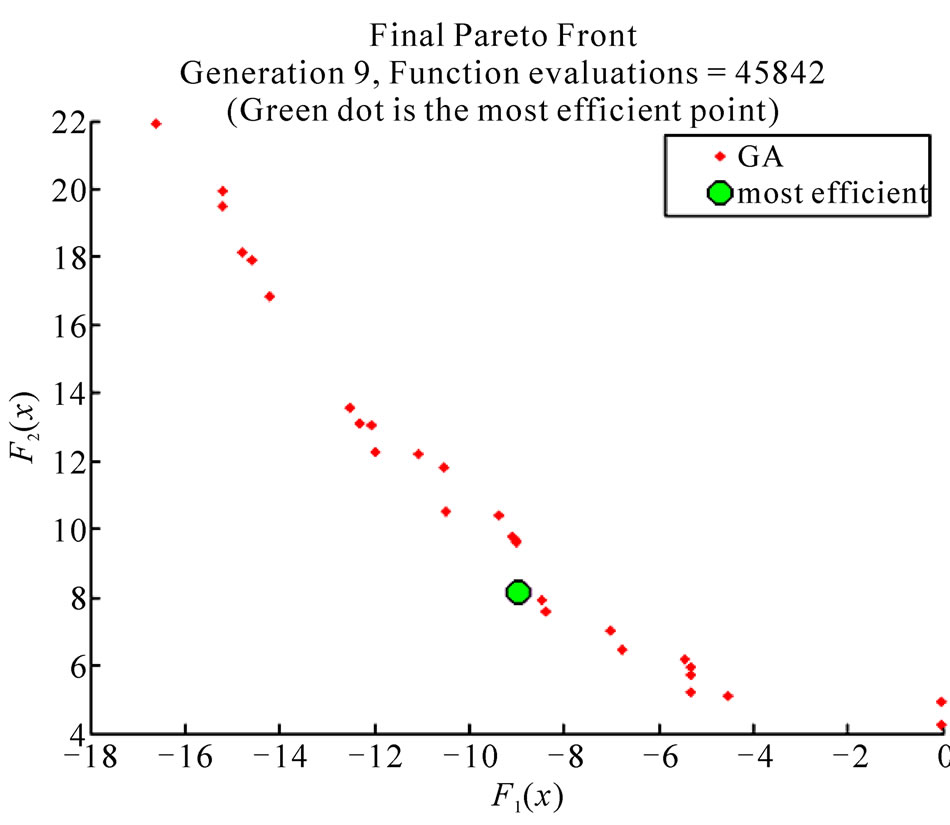
Figure 1. Final pareto front showing the scatter plot of the population members and the number of function evaluations using GA.
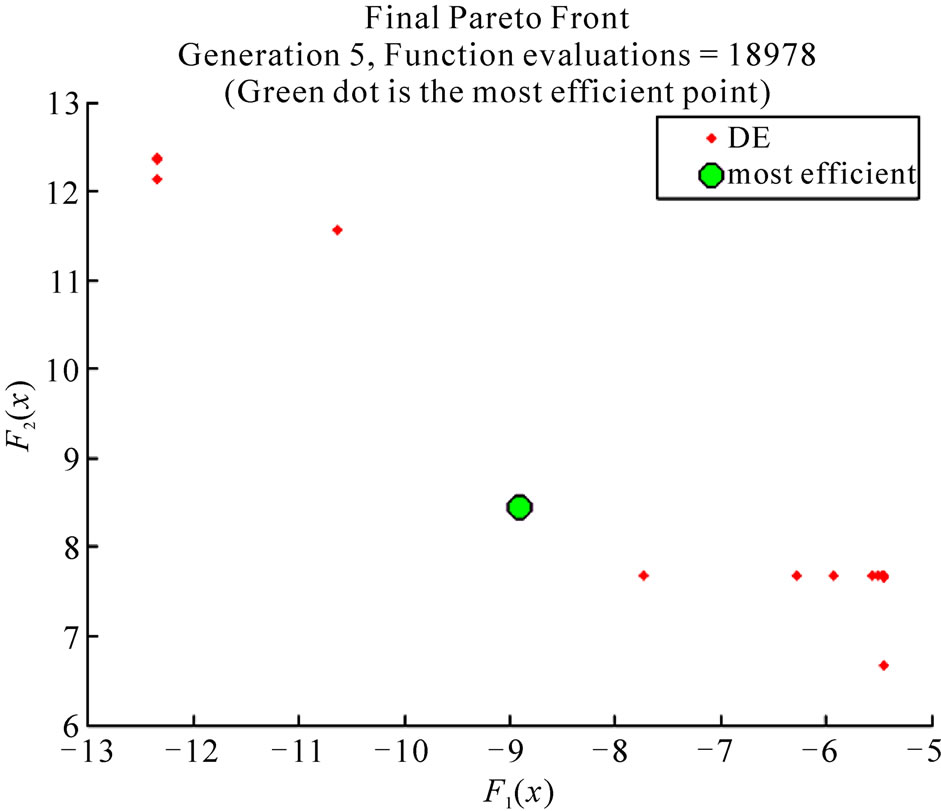
Figure 2. Final pareto front showing the scatter plot of the population members and the number of function evaluations using DE.
front after optimizing using DE, and the number of function evaluations required. The green dot in Figure 1 and 2, representing the optimum point, is arrived at as follows. Among the final population, the minimum value of F1(x) and the maximum value of F2(x) are used to fix an origin and the green dot or the optimum point is the point that has the minimum distance from the origin that was previously fixed.
In Figures 1 and 2,
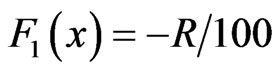
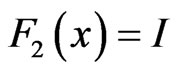
DE requires less than two times the number of function evaluations as GA and this was found to be consistent over a number of optimizations. This lesser number of function evaluations means that the computational cost of optimizing using DE is far less than GA.
5.2. Interference vs Throughput
Another parameter for comparing the performance is the throughput achieved for various values of aggregate interference. Figure 3 is the plot of interference vs. throughput for GA and DE, taking interference as the independent variable.
We can see from the graph that for most values of interference, the throughput obtained in the case of DE is greater than that of GA. This increased throughput for the same value of interference is favorable to the secondary user.
5.3. Localization of Best Solution
It can be seen from Figure 1 that the members of the final
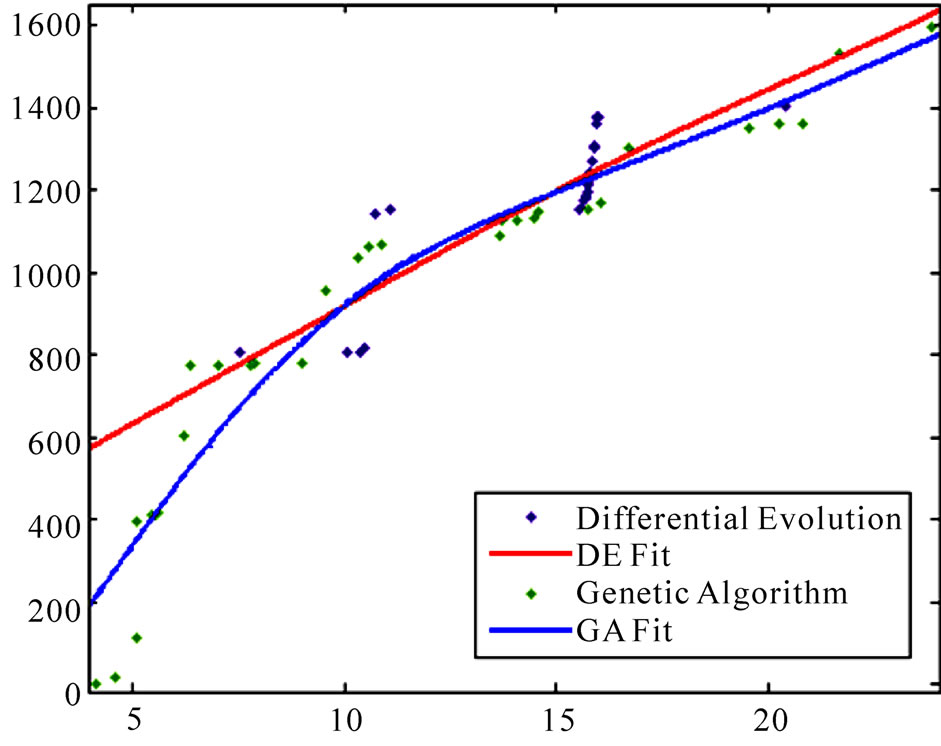
Figure 3. Plot of interference vs. throughput for the final population with interference as the independent variable, for both GA and DE.
population in GA are uniformly scattered and hence visually localizing the best member becomes difficult. However, in the case of DE, we can see that the best member can be easily localized. Figure 2 shows the scatter of the final population members of DE. Moving to the left from the green dot drastically increases the interference and moving to the right decreases the throughput significantly. Hence, no other point can possible be the best member.
From the above comparisons, DE has been found to be more advantageous than GA in the following ways.
1) The lesser number of function evaluations means that the rate of convergence is better in the case of DE than GA.
2) The higher throughput achieved means that DE converges to a better optimum value when compared to GA.
3) The accuracy of convergence is also evident from the scatter plots in Figures 1 and 2, since the best member is localized in the case of DE, whereas the same cannot be said for GA.
6. Conclusions
A cognitive radio network aims to maximize spectrum utilization by detecting unused spectrum and letting the secondary users utilize it. Setting the threshold for energy based spectrum sensing is a non-convex optimization process and the optimization should be such that the probability of error decreases. In this paper, we have first explained the sensing problem involved, the requirement of optimization and the objective functions. We have then stated the disadvantage of generic algorithms in these circumstances, which is the large number of iterations it takes to converge. We then propose a method for nonconvex threshold optimization using differential evolution and then compare the results obtained from differential evolution and genetic algorithms. Based on three factors, namely the number of function evaluations, the marginal increase in the throughput achieved and the easiness of localizing the best solution, we conclude that differential evolution has certain definite advantages over genetic algorithms in optimizing the threshold for energy based spectrum sensing.