Pullback Exponential Attractors for Nonautonomous Reaction Diffusion Equations in H01 ()
1. Introduction
Attractor’s theory is very important to describe the long time behavior of dissipative dynamical systems generated by evolution equations, and there are several kinds of attractors. In this article, we will study the existence of pullback exponential attractors (see [1]-[3]) for nonlinear reaction diffusion equation. This equation is written in the following form:
 (1.1)
(1.1)
where 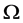 is a bounded smooth domain in
is a bounded smooth domain in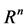 ,
, 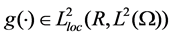 ,
, 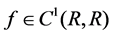 and there exist
and there exist 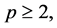
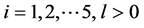
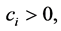 such that
such that
 (1.2)
(1.2)
for all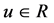 .
.
The Equation of (1.1) has been widely studied. For the autonomous case, i.e., 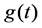 does not depend on the time, the asymptotic behaviors of the solution have been studied extensively in the framework of global attractor, see [4]-[6]. For the nonautonomous case, the asymptotic behaviors of the solution have been studied in the framework of pullback attractor, see [7]-[9]. Recently, the theory of pullback exponential attractor have been developed, see [1]-[3], and some methods are given to prove the existence of pullback exponential attractors.
does not depend on the time, the asymptotic behaviors of the solution have been studied extensively in the framework of global attractor, see [4]-[6]. For the nonautonomous case, the asymptotic behaviors of the solution have been studied in the framework of pullback attractor, see [7]-[9]. Recently, the theory of pullback exponential attractor have been developed, see [1]-[3], and some methods are given to prove the existence of pullback exponential attractors.
In order to obtain the existence of pullback exponential attractors of (1.1), we will need the following theorem.
Theorem 1.1. ([3]) Let 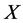 be an uniformly convex Banach space,
be an uniformly convex Banach space, ![]() be the set of all bounded subsets of
be the set of all bounded subsets of ![]()
![]() be a time continuous process in
be a time continuous process in![]() . Then the process
. Then the process ![]() exist pullback exponential attractors in
exist pullback exponential attractors in ![]() if the following conditions hold true:
if the following conditions hold true:
(1) There exists an uniformly bounded absorbing set![]() , that is, for any
, that is, for any ![]() and
and![]() , there exists
, there exists ![]() such that
such that
![]() (1.3)
(1.3)
(2) There exist![]() , and a finite dimension subspace
, and a finite dimension subspace![]() , such that
, such that
![]() (1.4)
(1.4)
![]() (1.5)
(1.5)
![]() (1.6)
(1.6)
for all ![]() and
and![]() , where
, where ![]() is independent on the choice of
is independent on the choice of![]() , and
, and ![]() is the norm in
is the norm in![]() ,
, ![]() is the identity operator,
is the identity operator, ![]() is a bounded projector,
is a bounded projector, ![]() is the dimension of
is the dimension of![]() .
.
2. Some Estimates of Equation (1.1)
In this section, we will derive some priori estimates for the solutions of (1.1) that will be used to construct pullback exponential attractors for the problem (1.1).
For convenience, hereafter let ![]() be the norm of
be the norm of ![]() and
and ![]() an arbitrary constant, which may difference from line to line and even in the same line. We define
an arbitrary constant, which may difference from line to line and even in the same line. We define ![]() with scalar product
with scalar product ![]() and norm
and norm
![]() ; let
; let ![]() and
and ![]() denote the scalar product and norm of
denote the scalar product and norm of ![]() and
and ![]() for all
for all![]() , set
, set ![]() is the first eigenvalue of
is the first eigenvalue of![]() .
.
For the initial value problem (1.1), we know from [4]-[6] that for any initial datum![]() , there exists a unique solution
, there exists a unique solution ![]() for any
for any![]() .
.
Thanks to the existence theorem, the initial value problem is equivalent to a process ![]() define by
define by
![]() .
.
In addition, we assume that the function ![]() is translation bounded in
is translation bounded in![]() , that is
, that is
![]() (2.1)
(2.1)
By (2.1), for![]() , we have
, we have
![]() (2.2)
(2.2)
Lemma 2.1. ([7]-[9]) Assume that ![]() satisfy (1.2) and (2.2),
satisfy (1.2) and (2.2), ![]() be a weak solution of (1.1), then for any
be a weak solution of (1.1), then for any![]() , we have the following inequality:
, we have the following inequality:
![]() (2.3)
(2.3)
and
![]() (2.4)
(2.4)
Lemma 2.2. Assume that ![]() satisfy (1.2) and (2.2),
satisfy (1.2) and (2.2), ![]() be a weak solution of (1.1), then the following inequality holds for
be a weak solution of (1.1), then the following inequality holds for ![]()
![]() (2.5)
(2.5)
Obviously, for any bounded![]() , there exist
, there exist![]() , such that
, such that
![]() for any
for any ![]() and
and![]() . (2.6)
. (2.6)
Proof. Let![]() , then by (1.2), we get there exist
, then by (1.2), we get there exist![]() ,
, ![]() , such that
, such that
![]() . (2.7)
. (2.7)
Taking inner product of (1.1) with ![]() in
in ![]() and using (2.7), we get
and using (2.7), we get
![]() . (2.8)
. (2.8)
Multiply (1.1) by![]() , we have
, we have
![]()
since![]() , we obtain
, we obtain
![]() .
.
Combining (2.7), we get
![]() . (2.9)
. (2.9)
Thanks to Poincaré inequality![]() , we have
, we have
![]() . (2.10)
. (2.10)
Let![]() , by (2.9) and (2.10), we obtain
, by (2.9) and (2.10), we obtain
![]() ,
,
which imply
![]() ,
,
integrating, we get
![]() ,
,
using (2.3) and (2.4), we get the inequality (2.5).
Lemma 2.3. Assume that ![]() satisfy (1.2) and (2.1),
satisfy (1.2) and (2.1), ![]() be a weak solution of (1.1), then the following inequality holds for
be a weak solution of (1.1), then the following inequality holds for ![]()
![]() , (2.11)
, (2.11)
Here ![]() for any
for any![]() .
.
By the assumption (2.1) and for![]() , we get
, we get
![]() . (2.12)
. (2.12)
Proof. Multiply (1.1) with![]() , we obtain
, we obtain
![]() . (2.13)
. (2.13)
By (1.2) and Young’s inequality, we have
![]() ,
,![]() .
.
By (2.13), we get
![]()
integrating and using (2.4), we get
![]() . (2.14)
. (2.14)
Multiply (1.1) with![]() , we obtain
, we obtain
![]() .
.
By (2.1), we get
![]() .
.
Using Young’s inequality
![]() .
.
By the above inequality, we have
![]()
integrating and using (2.12) and (2.14), we get (2.11) holds.
Lemma 2.1, lemma 2.2 and lemma 2.3 show that the process generated by the equation (1.1) have an uniformly pullback bounded absorbing set in![]() , that is
, that is
Theorem 2.4. Assume that ![]() satisfy (1.2) and (2.1),
satisfy (1.2) and (2.1), ![]() be a weak solution of (1.1), then the process generated by the equation (1.1) have an uniformly pullback bounded absorbing set
be a weak solution of (1.1), then the process generated by the equation (1.1) have an uniformly pullback bounded absorbing set ![]() , that is, for any bounded set
, that is, for any bounded set![]() , there exists
, there exists![]() , such that
, such that ![]() for any
for any![]() .
.
In fact, using the same proof as in Lemma 2.3, we can get the following result.
Lemma 2.5. Assume that ![]() satisfies (1.2),
satisfies (1.2), ![]() is translation bounded in
is translation bounded in![]() , that is
, that is ![]()
![]() be a weak solution of (1.1), then the process generated by the equation (1.1) have
be a weak solution of (1.1), then the process generated by the equation (1.1) have
an uniformly pullback bounded absorbing set![]() , that is, for any bounded set
, that is, for any bounded set![]() , there exists
, there exists![]() , such that
, such that ![]() for any
for any![]() .
.
3. Pullback Exponential Attractors
In this section, we will use Theorem 1.1 to prove that the process generated by Equation (1.1) exists a pullback exponential attractor.
First we assume that the function ![]() is normal ([10]) in
is normal ([10]) in![]() , that is, for any
, that is, for any![]() , there exists
, there exists ![]() such that
such that
![]() . (3.1)
. (3.1)
Obviously, ![]() is normal in
is normal in ![]() implying that
implying that ![]() is translation bounded in
is translation bounded in![]() .
.
We set![]() , since
, since ![]() is a continuous compact operator in
is a continuous compact operator in![]() , by the classical spectral theorem, there exist a sequence
, by the classical spectral theorem, there exist a sequence![]() ,
, ![]() and a family of elements
and a family of elements ![]() of
of
![]() which are orthogonal in
which are orthogonal in ![]() such that
such that![]() ,
,![]() . Let
. Let ![]() in
in ![]() and
and ![]() is a orthogonal projector. For any
is a orthogonal projector. For any![]() , we write
, we write
![]() .
.
Theorem 2.4. Assume that ![]() satisfies (1.2),
satisfies (1.2), ![]() is translation bounded in
is translation bounded in ![]() and (3.1) holds, then the process generated by the equation (1.1) have a pullback exponential attractor.
and (3.1) holds, then the process generated by the equation (1.1) have a pullback exponential attractor.
Next, we will verify that the process generated by (1.1) satisfy all the conditions of Theorem 1.1.
Proof. By Theorem 2.4, there exists![]() , such that
, such that ![]() for any
for any![]() . Let
. Let![]() , we obtain
, we obtain ![]() is also an uniformly pullback bounded absorbing set in
is also an uniformly pullback bounded absorbing set in ![]() and
and ![]() for any
for any![]() .
.
We set![]() ,
, ![]() to be solutions associated with Equation (1.1) with initial data
to be solutions associated with Equation (1.1) with initial data![]() , since
, since ![]() is the uniformly pullback bounded absorbing set in
is the uniformly pullback bounded absorbing set in![]() , so there exists
, so there exists ![]() such that
such that![]() ,
, ![]() Let
Let![]() , by (1.1), we get
, by (1.1), we get
![]() (3.2)
(3.2)
Taking inner product of (3.2) with ![]() in
in![]() , we have
, we have
![]() (3.3)
(3.3)
Taking into account (1.2) and Holder inequality, it is immediate to see that
![]() ,
,
and
![]()
By Lemma 2.5, we get
![]() (3.4)
(3.4)
Using (3.3), we obtain![]() , hence
, hence
![]() . (3.5)
. (3.5)
Let![]() ,
, ![]() be the project in
be the project in![]() . Taking inner product of (3.2) with
. Taking inner product of (3.2) with ![]() in
in![]() , we have
, we have
![]() . (3.6)
. (3.6)
![]() .
.
Taking into (3.4) account, we obtain
![]() ,
,
Using the Poincaré inequality![]() , we get
, we get![]() , by Gronwall’s Lemma, we have
, by Gronwall’s Lemma, we have![]() . Using (3.5), we get
. Using (3.5), we get
![]() . (3.7)
. (3.7)
Let![]() ,
, ![]() be the project in
be the project in![]() . Taking inner product of (1.1) with
. Taking inner product of (1.1) with![]() , we get
, we get
![]()
Since![]() ,
, ![]() , and by Poincaré inequality
, and by Poincaré inequality![]() , we have
, we have
![]()
By Gronwall’s lemma, we get
![]() .
.
By (3.1), we obtain that there exists![]() , such that
, such that ![]() for any
for any![]() , and for any
, and for any![]() , there exists
, there exists![]() , such that
, such that![]() , so we get
, so we get
![]() and
and![]() , we have
, we have
![]() (3.8)
(3.8)
Let![]() , by (3.5), we get
, by (3.5), we get
![]() (3.9)
(3.9)
Since![]() , for
, for![]() , from (3.7) and (3.8), there exist
, from (3.7) and (3.8), there exist![]() ,
, ![]() such that
such that
![]() (3.10)
(3.10)
![]() (3.11)
(3.11)
By Theorem 2.4 and (3.9)-(3.11), we know that the process ![]() generated by (1.1) satisfy all the conditions of Theorem 1.1.
generated by (1.1) satisfy all the conditions of Theorem 1.1.
Funds
This work was supported by the National Nature Science Foundation of China (11261027) and Longyuan youth innovative talents support programs of 2014, and the innovation Funds of principal (LZCU-XZ2014-05).