A Study of Some Nonlinear Partial Differential Equations by Using Adomian Decomposition Method and Variational Iteration Method ()
1. Introduction
In this paper, we discuss the solution of the nonlinear BBM equation [1]
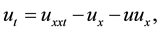 (1)
(1)
subject to the initial condition
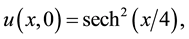 (2)
(2)
The Cahn-Hilliard equation [2] :
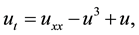 (3)
(3)
subject to the initial condition
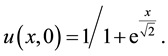 (4)
(4)
[3] [4] derived a variety of exact travelling wave solutions of distinct physical structures for the BBM equation, where the Tanh and the sine-cosine methods were used. Also [5] is devoted to analyzing the physical structures of the nonlinear dispersive variants of the BBM equation, where new exact solutions with compact and noncompact structures for BBM are derived. [6] applied the decomposition method to obtain explicit and numerical solutions of different types of generalized BBM. Many articles have investigated Cahn-Hilliard equation analytically and numerically, [7] applied the finite difference method to obtain the numerical solution of Cahn-Hilliard equation. [8] - [10] used the Exp-function method to obtain exact solutions of Cahn-Hilliard. [11] solved these equations by Differential Transform Method.
In the beginning of the 1980, a so-called Adomiande composition method (ADM), which appeared in [12] -[15] used (ADM) to solve coupled kdv equation.
2. The Adomian Decomposition (ADM)
In this section, ADM is explained. For this, we consider a general nonlinear partial differential equation in the following form.
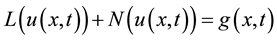 (5)
(5)
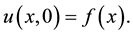 (6)
(6)
where 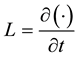 which is assumed easily invertible,
which is assumed easily invertible, 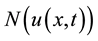 presents the nonlinear term and g is the source term. Appling the inverse operator
presents the nonlinear term and g is the source term. Appling the inverse operator 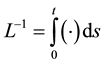 to both sides of (5) and using the given conditions we obtain
to both sides of (5) and using the given conditions we obtain
 (7)
(7)
using the given conditions, the ADM defines the solution u by the series in the following form.
 (8)
(8)
and the nonlinear operator  presents by an infinite series of the so-called Adomian’s
presents by an infinite series of the so-called Adomian’s
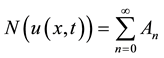 (9)
(9)
where 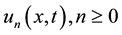 are the components of
are the components of 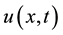 that will be easy determined and
that will be easy determined and 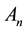 are called Adomian’s polynomials and defined by
are called Adomian’s polynomials and defined by
![]() (10)
(10)
From the above considerations, the decomposition method defines the components ![]() for
for![]() ,
,
by the following recursive relationships,
![]() (11)
(11)
![]() (12)
(12)
Finally, the approximate solution for u(x, t) is obtained by truncating the series
![]() (13)
(13)
For more details about ADM and its convergence, see [12] - [14] [16]
Now, we first consider a general form of nonlinear equation
![]() (14)
(14)
Second, we introduce the wave variable
![]() (15)
(15)
so that
![]() (16)
(16)
the PDF (14) convert to an ODE
![]() (17)
(17)
3. Application of ADM
In this article, we investigate some example of the nonlinear partial differential equations
3.1. Benjamin-Bona-Mahony
![]() (18)
(18)
subject to the initial condition
![]() (19)
(19)
with the exact solution is
![]() (20)
(20)
By using (15), Equations (18) and (19) converted to the ODE
![]() (21)
(21)
subject to the initial conditions
![]() (22)
(22)
Applying the ADM to (21)-(22), we obtain
![]() (23)
(23)
![]() (24)
(24)
we apply the inverse operator ![]() on both sides (24) we get
on both sides (24) we get
![]() (25)
(25)
where the components of ![]() are the so-called Adomian polynomials, for each
are the so-called Adomian polynomials, for each ![]() depends on
depends on
![]()
![]() (26)
(26)
The components ![]() can be computed as
can be computed as
![]() (27)
(27)
![]() (28)
(28)
Then,
![]() (29)
(29)
Then approximation solution of Equation (18) is ![]() with third-order approximation. Now we compare exact solution with Adomain Decomposition Method (ADM) solution in Figure 1.
with third-order approximation. Now we compare exact solution with Adomain Decomposition Method (ADM) solution in Figure 1.
3.2. The Cahn-Hilliard Equation
![]() (30)
(30)
subject to the initial condition
![]() (31)
(31)
![]()
Figure 1. Exact and approximate solutions to BBM equation by ADM when ![]()
where the exact solution is
![]() (32)
(32)
By using (15), Equations (30) and (31) converted to the ODE
![]() (33)
(33)
subject to the initial conditions
![]() (34)
(34)
Applying the ADM to (33)-(34), we get
![]() (35)
(35)
![]() (36)
(36)
we apply the inverse operator ![]() on both sides (36) we have
on both sides (36) we have
![]() (37)
(37)
![]() (38)
(38)
where the components of ![]() are the so-called Adomian polynomials, for each
are the so-called Adomian polynomials, for each ![]() depends on
depends on
![]()
![]() (39)
(39)
The components ![]() can be computed as
can be computed as
![]() (40)
(40)
![]() (41)
(41)
![]() (42)
(42)
Then approximation solution of Equation (30) is ![]() . Now we compare exact solution with Adomain Decomposition Method (ADM) solution in Figure 2.
. Now we compare exact solution with Adomain Decomposition Method (ADM) solution in Figure 2.
4. Variational Iteration Method (VIM) [17]
Let consider the differential equation
![]() (43)
(43)
where L and N are linear and nonlinear operators, respectively, and ![]() is the inhomogeneous term. In the
is the inhomogeneous term. In the
![]()
Figure 2. Exact and approximate solutions to Cahn-Hilliard equation by ADM when ![]()
references [18] , a correction functional for Equation (43) can be written as
![]() (44)
(44)
where ![]() is a general Lagrange’s multiplier [17] , which can be identified optimally via the variational theory, and
is a general Lagrange’s multiplier [17] , which can be identified optimally via the variational theory, and ![]() is are stricted variation which means
is are stricted variation which means![]() . The successive approximations
. The successive approximations![]() , of the solution u will be readily obtained upon using the determined Lagrangian multiplier and any selective function
, of the solution u will be readily obtained upon using the determined Lagrangian multiplier and any selective function![]() . Therefore, the solution is given by
. Therefore, the solution is given by
![]()
5. Application of VIM
Considering the BBM Equation (18, 19, 20)
![]()
The VIM can be applied to Equation (18) in the form
![]() (45)
(45)
where λ yields to ?1. One can substitute above λ and use the initial approximation as in Equation (45) to get the successive approximation by the following expressions:
![]() (46)
(46)
![]() (47)
(47)
![]() (48)
(48)
![]() (49)
(49)
The Cahn-Hilliard equation:
![]()
the VIM can be applied to Equation (30) in the form
![]() (50)
(50)
where λ yields to ?1. One can substitute above λ and use the initial approximation as in Equation (50) to get the successive approximation by the following expressions:
![]() (51)
(51)
![]() (52)
(52)
![]() (53)
(53)
6. Conclusion
In this work, the Adomian Decomposition Method and the Variational Iteration Method have been successfully applied to find the solution of nonlinear Benjamin-Bona-Mahony and Cahn-Hilliard equations are presented in Figures 1-4. It was observed that the use of ADM and VIM provides a very good estimation when compared
![]()
Figure 3. Exact and approximate solutions to BBM equation by VIM when![]()
![]()
Figure 4. Exact and approximate solutions to Cahn-Hilliard equation by VIM when ![]()
with exact values. These methods convert these equations to recurrences relation whose terms are computed using maple 15. This method is very effective and accelerates the convergent of solution.