Modern Ab-Initio Calculations on Modified Tomas-Fermi-Dirac Theory ()
1. Introduction
Thomas-Fermi theory is originally proposed by Thomas and Fermi [1] - [4] to describe the electron shell of a heavy atom, which is characterized by a relatively uniform distribution of the electron density.
Thomas-Fermi theory is the semi-classical (WKB) limit in relation to self-consistent Hartree field equations, and therefore the modification of this model is associated with a more detailed account of the correlation, exchange, quantum and multi-shell effects.
Initial approximate nature of Thomas-Fermi theory has a dual nature. Remain outside the model, firstly, correlation effects, reflecting the inaccuracy of the Hartree method and the associated self-consistent difference (average) true interaction from the true physical interaction. Secondly, in Thomas-Fermi theory quantum effects are not considered responsible approximate nature of the semi-classical description of the atom. The report examines the theory of these effects, allowing to find the limits of applicability of Thomas-Fermi theory in its original form and to generalize the model beyond the scope of its applicability.
The presence of correlation corrections is caused by difference of self-consistent Hartree field of the actual field inside the atom. These corrections are the result of the anti-symmetry of the electron wave functions and are interpreted as the exchange correlation effects. Additionally, appear also the effects of the power correlation.
We begin by considering the effects of correlation, which in turn are divided into two classes. This is primarily the effects of statistical correlation (exchange effects), describing the effect of the Pauli principle on the interaction of particles. Electrons with parallel spins are hold at a greater distance from each other than in the singlet state, and the radius of such a correlation coincides with the de Broglie wavelength of an electron.
Correlation effects of the second class (called correlation effects of power or simply correlation effects) reflect the inaccuracy of the principle of independent particles, i.e., the inability to talk about the state of a single electron in the effective average field of the other particles because of their mutual influence, beyond the self-consistent description. Being the power effects, this kind of correlation effects characterized by a dimensionless parameter is equal to the ratio of perturbation theory of the average energy of the Coulomb interaction between pairs of particles to their average kinetic energy. In Thomas-Fermi [3] [4] theory which introduces accounting Dirac correlation effects [2] , this expansion has been called the theory of Thomas-Fermi-Dirac.
The report shows that the total energy of the electrons can be expressed in terms of the spatial dependence of the electron density according to the Thomas-Fermi-Dirac theory. In report calculation, the energy of the atom is based on nuclear-electron and electron-electron interactions (which can also be represented as a function of the electron density).
Quantum corrections arise from the use of the semi-classical formalism and reflect the presence of non-local electron density communication to the potential in consequence of the “uncertainty principle”.
2. Theoretical Procedures
A variational technique can be used to derive the Thomas-Fermi equation, and an extension of this method provides an often-used and simple means of adding corrections to the statistical model [5] [6] . Thus, we can write the Fermi kinetic energy density of a gas of free electrons at a temperature of zero degrees absolute in the form:
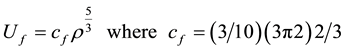
The electrostatic potential energy density is the sum of the electron-nuclear and the electron-electron terms. We can write this as:
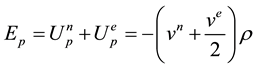 ,
,
where vn is the potential due to the nucleus of charge Z, ve is the potential due to the electrons, and the factor of 1/2 is included in the electron-electron term to avoid counting each pair of electrons twice.
With x denoting distance from the nucleus, the total energy of the spherical distribution is given by
 (1)
(1)
The expression for density on the Thomas-Fermi model,
 (2)
(2)
with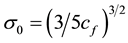 , is obtained by minimizing Equation (1) subject to the auxiliary condition that the total number of particles N, remains constant.
, is obtained by minimizing Equation (1) subject to the auxiliary condition that the total number of particles N, remains constant.
The potential energy V, is a function of position in the electron distribution. E’ is the Fermi energy, or chemical potential, and is constant throughout a given distribution. The Thomas-Fermi equation follows from Equation (2) and Poisson’s equation.
The tendency for electrons of like spin to stay apart because of exclusion principle is accounted for by the inclusion in Equation (1) of exchange energy, the volume density of which is given by:

Minimization of the total energy now leads to the equation:
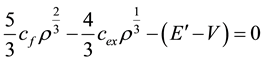
Which is quadratic in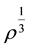 . From this equation we get
. From this equation we get
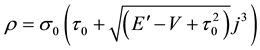 ,
,
where
 (3)
(3)
Now Poisson equation with the density given by Equation (3) leads to the Thomas-Fermi-Dirac (TFD) equation. In the following two slides we propose additional energy terms to be included in Equation (l). The incorporation of these terms leads to a simple quantum-and correlation-corrected TFD equation.
The quantum-correction energy density follows from a slight change in the derivation due to March and Plaskett [6] . March and Plaskett have demonstrated that the TF approximation to the sum of one-electron eigenvalues in a spherically symmetric potential is given by the integral:
 (4)
(4)
where the number of states over which the sum is carried is written as
 (5)
(5)
Here E(nr, l) is the expression for the WKB (quasi-classic) eigen-values considered as functions of continuous variables [1] [6] ;
nr is the radial quantum number;
l is the orbital quantum number;
And the region of integration is bounded by nr = −1/2, l = −1/2, and E(nr, l) = E'.
We have included a factor of two in these equations to account for the spin degeneracy of the electronic states. The Fermi energy E' is chosen so that Equation (5) gives the total number of states being considered, the N electrons occupying the N lowest states. With considerable manipulation, Equation (4) becomes TF energy equation:
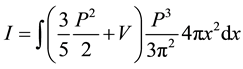 (6)
(6)
and Equation (5) reveals the TF density through the expression
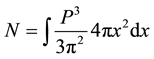 (7)
(7)
both integrals being taken between the roots of E' = V(x). We have written these results in atomic units, so that P, the Fermi momentum, is defined by

It is pertinent to examine the error in the TF sum of eigen-values, as given by Equation (6), for case of pure Coulomb field. The WKB eigen-values in Coulomb field given by
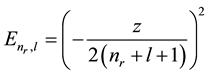 (8)
(8)
And let us consider the levels filled from n = 1 to n = v, where n is the total quantum number defined by n = nr + l + 1. Then, for any value of v we can evaluate the error in the TF approximation to the sum of eigen-values, comparing always with the correct value, −Z2v. Scott correction to the total binding energy is obtained by letting v become very large.
Although the sum of one-electron eigen-values is not the total energy of the statistical atom because of the electron-electron interaction being counted twice, we might expect to improve the calculated binding energy greatly by correcting this sum in some manner, since the chief cause of the discrepancy is certainly the large error in the electron-nuclear potential energy.
This correction can be performed by imposing a new lower limit on l in the integrations above. When we introduce a new lower limit lmin and a related quantity which we call the “modification factor”,
![]()
we obtain, after more manipulation, slightly different expressions corresponding to Equation (6) and Equation (7).
From these revised expressions we can identify a quantum-corrected TF density expression,
![]() (9),
(9),
and corrected kinetic energy density
![]() (10)
(10)
Revised lower limit on the volume integrals, say x1, is the lower root of
![]() (11)
(11)
for x < xl, ρ must vanish (stay zero), and we have thus termed x1 the “inner density cutoff distance”.
We can call the second term on the right-hand side of Equation (10) the “quantum-correction energy density” and write it in the more consistent form:
![]() (12)
(12)
The modification factor a, is determined by the initial slope of the potential function.
For interpreting these results it is helpful to consider just what we have done in changing the lower limit of the orbital quantum number.
Since the lower limit l = −1/2 must correspond to an orbital angular momentum of zero, we have, clearly, eliminated states with angular momentum of magnitude between zero and a cutoff value Lc = aħ. Corresponding to Lc at every radial distance is now a linear cutoff momentum: Pc = aħ/x, and we can rewrite Equation (9) in terms of the Fermi momentum and cutoff momentum:
![]() (13)
(13)
At radial distances less than xl, momenta are prohibited over the entire range from zero to P, so the electron density vanishes. This interpretation must be modified somewhat when exchange and correlation effects are included; for then the Fermi momentum is no longer simply given by Equation (8), except very near the nucleus.
We can define x1 as in the absence of interactions, i.e., as the lower of the roots of Equation (11), but it is not correct to demand that the density vanish at the upper root. Instead, we require only that the density be real.
Correlation Correction [1] [5] [6] . The original TF equation describes a system of independent particles, while the introduction of exchange energy, which leads to the TFD equation, represents a correction for the correlated motion of electrons of like spin. The remainder of the energy of the electron gas is termed the correlation energy. By its inclusion we are recognizing that electrons, regardless of spin orientation, tend to avoid one another.
In extensions of the statistical model there have been suggested at least two different expressions, for the correlation energy that approach, in the appropriate limits, Wigner’s low-density formula and the expression due to Gell-Mann and Brueckner at high densities. In addition to these, Gombas and Tomishima [6] have utilized expansions of the correlation energy per particle in powers of ρ1/3 about the particle density encountered at the outer boundary of the atom or ion. In this expansion, the term of first-order can be considered as a correction to the exchange energy, and it follows that the TFD solutions for a given Z then correspond to correlation-corrected solutions for a modified value of Z.
Aside from rather poor approximation of the correlation energy, a drawback to this procedure is that the TFD solutions must be at hand. If solutions representing specified degrees of compression are desired, the method would appear to be impractical. It is interesting and fortunate that over density range of interest it is apparently possible to approximate the correlation energy per particle quite closely by an expression of form:
![]()
where we have set cc = 0.0842, and compared this approximation with the values due to Carr and Maradudin [5] .
3. Derivation and Discussion
From the results of the preceding slides, we can now express the total energy per unit volume of the charge distribution in the form:
![]() (14)
(14)
where all quantities appearing in the equation have been previously defined. By minimizing the integral of U over the volume occupied by the charge, while requiring that the total number of electrons be fixed, we obtain the following equation:
![]()
where ![]()
The electron density is found as a function of R by solving Equation (14), a quartic in ρ1/6.
To accomplish this we write a “resolvent cubic equation” in terms of another variable, say y:
![]() (15)
(15)
Let us use the same symbol y, to denote any real root of this cubic equation.
We can then express the four roots of the quartic, and hence four expressions for the electron density, in terms of y. One of these expressions possesses the proper behavior in reducing to previously obtained results in the neglect of correlation and exchange effects, namely:
![]() (16)
(16)
where
![]() (17)
(17)
We note that ψ vanishes when correlation is neglected, since y = −τ1 is then root of Equation (15). In the familiar manner we now define a modified TFD potential function θ by the relation:
![]() (18)
(18)
and from Poisson equation and Equation (16) we obtain:
![]() (19)
(19)
in terms of θ:
![]() (20)
(20)
Equation (20), Equation (15), Equation (17), and Equation (19) constitute the differential relationship to be satisfied at each step in the integration. We could, of course, write immediately the solutions of Equation (15) in analytic form, but it proves convenient in the numerical treatment to obtain a root by the Newton-Raphson method, since a good first guess in the iteration is available from the previous integration step.
The boundary conditions on Equation (19) are:
First―as nucleus approached the potential must become that nucleus alone, or θ(0) = 1;
Second―at outer boundary x2, of distribution of N electrons,
![]()
Integration by parts yields:
![]()
we have the usual condition:
![]() (21)
(21)
In addition to potential and density distributions, total binding energies of atoms are of special interest to us here. For the proper evaluation of energies, the arbitrary constant that is present originally in both the electrostatic potential energy and the Fermi energy must be specified. The state of infinite separation of the constituent particles is normally taken to have zero energy.
We therefore follow the usual convention and fix the potential at the edge of the neutral atom at zero for all values of x2. For an ion the potential energy of an electron at the boundary is taken as:
![]()
The defining relation, Equation (18), now gives at the boundary:
![]()
or, solving for the Fermi energy,
![]()
The total electron-nuclear potential energy given by
![]()
While for the electron-electron potential energy we have
![]()
From Equation (18) and the relation![]() , this becomes:
, this becomes:
![]()
Other energy integrals are, with an obvious notation:
![]()
4. Results and Conclusions
It was pointed out in the introduction that the quantum-corrected TFD equation yields atomic binding energies in good agreement with experimental values and with the results of Density Functional Theory (DFT) calculations [5] .
Multi-shells effects reflect irregularities physical quantities due to the discrete energy spectrum, but in the case of the continuous spectrum of these effects may occur as a result of interference of de Broglie waves and allow the model to take into account the shells structure of the atom. Multi-shells effects associated with the discrete spectrum of bound electrons in atomic systems (atom, ion, atomic cell, etc.).
Multi-shells effects, unlike quantum-exchange effects, affect to the chemical potential E', but practically have no effect on the value of self-consistent potential V [7] . Therefore, when they account for the calculation of a corresponding shells correction is not necessary to solve the Poisson equation. Just use the normalization condition with the same self-consistent potential in Thomas-Fermi model.
For shell corrections E'sh primary role of shell effects reduces to a shift of the chemical potential E' [8] ,
![]()
where v = nr + 1/2, λ = l + 1/2.
Software implementation of this modified Thomas-Fermi theory and calculations (for example, rare gas atoms, Table 1 and Table 2) taking into account quantum, exchange and correlation corrections showed that the this
![]()
Table 2. The electron density (external shells) of the rare atoms―helium, neon, argon, krypton, computed on the present model agree closely with their crystal radii.
corrections really lead to a rapprochement and converge results with experimental data, and also the results obtained by the DFT approximation [5] . Total energy calculations by Thomas-Fermi, DFT and experimental data are shown in the summary Table 1. Next step of this work is included program realization for multi-shell and gradient corrections also [1] [6] .
Acknowledgements
“Keldysh Institute of Applied Mathematic”, Moscow, Russian Federation;
“Tohocu University”, Sendai city, Japan;
“Los Alamos Scientific Laboratory”, Oakland, USA.