The Tangential Force Distribution on Inner Cylinder of Power Law Fluid Flowing in Eccentric Annuli with the Inner Cylinder Reciprocating Axially ()
1. Introduction
At present in our country, there is few theoretical research on the tangential force on the wall of the inner cylinder of the power law fluid flowing in eccentric annuli with the inner cylinder reciprocating axially. This force for sucker rod eccentric wear research has an important influence. Therefore, research on the tangential force has a practical significance. Based on the governing equations of the inner cyinder of the unsteady flow of the power law fluid in eccentric annuli with the inner cylinder reciprocating axially in the bipolar coordinate system [1] , the calculation formulae of tangential force are established; the relevant numerical calculation method is given; and taking the aqueous solution of partially hydrolyzed HPAM for examples, the tangential forces are calculated and analyzed in this article.
2. Mathematical Models
2.1. Assumed Condition
Power law fluid with the inner cylinder reciprocating axially, 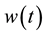 is axial velocity, T is the motion cycle, Ro is the radius of the inner cylinder of annuli, Ri is the radius of the inner cylinder, e is the eccentricity of the eccentric annulus.
is axial velocity, T is the motion cycle, Ro is the radius of the inner cylinder of annuli, Ri is the radius of the inner cylinder, e is the eccentricity of the eccentric annulus.
2.2. Governing Equations
The governing equations of the unsteady flow of the power law fluid in eccentric annuli with the inner cylinder reciprocating axially in the bipolar coordinate system by Haiqing Cui, Tao Gao [1] -[3] .
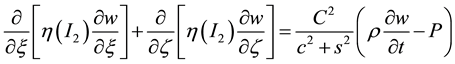 ( 1a )
( 1a )
2.3. Initial Conditions and Boundary Conditions
By assumption flow conditions can be obtained the boundary conditions of dynamic flow equation.
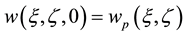 (1b)
(1b)
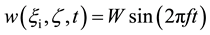 ( 1c )
( 1c )
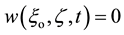 (1d)
(1d)
where 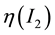 is the viscosity function of the power law fluid;
is the viscosity function of the power law fluid;  is the second invariant of the component of the first order Rivlin-Ericksen tensor;
is the second invariant of the component of the first order Rivlin-Ericksen tensor; ,
, 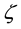 are the dipolar coordinates, and
are the dipolar coordinates, and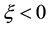 ,
,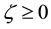 ;
; 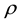 is the density of the power law fluid; t is the time; p is the pressure gradient;
is the density of the power law fluid; t is the time; p is the pressure gradient; 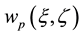 is the velocity distribution of the power law fluid in eccentric annuli with the motionless inner cylinder; W is the amplitude of the velocity of the inner cylinder reciprocating axially; f is the stroke frequency of the inner cylinder.
is the velocity distribution of the power law fluid in eccentric annuli with the motionless inner cylinder; W is the amplitude of the velocity of the inner cylinder reciprocating axially; f is the stroke frequency of the inner cylinder.
2.4. Tangential Force on the Wall of the Inner Cylinder
From the formulae of shear stress on the wall of the inner cylinder
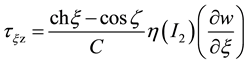 (2)
(2)
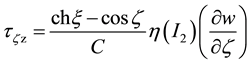 (3)
(3)
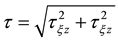 (4)
(4)
the calculation formulae of tangential force are given as follows
![]() (5)
(5)
which can be expressed as
![]() (6)
(6)
where
![]() (7)
(7)
3. Calculation Method
From the density of the power law fluid ρ, the flow behavior index of the power law fluid n, the consistency coefficient of the power law fluid k, the radius of the inner cylinder of annuli Ro, the radius of the inner cylinder Ri, the eccentricity of the eccentric annulus e, the stroke S, the stroke frequency of the inner cylinder f and the pressure gradient P, the distribution of the tangential force Fz can be calculated: firstly, through the equations (
1a
), (1b), (
1c
) and (1d), the velocity distribution of the power law fluid at anytime by using the finite difference method is calculated; then, through the formula (6), the tangential force by using the numerical integration method is calculated.
4. Calculation Examples
Take HPAM aqueous solution as an example, the radius of the inner cylinder of annulus Ro = 2.960 × 10−2 m, the radius of the inner cylinder Ri = 0.885 × 10−2 m, the pressure gradient of the aqueous solution P = 61.061 Pa/m and by using the calculation method mentioned above, the tangential forces on the wall of the inner cylinder of the HPAM aqueous solution are calculated and the relevant distribution curves are plotted as Figure 1 to Figure 4 (the minus of the tangential force indicates that the inner cylinder moves upwards).
Under different flow behavior index n, the curves of the tangential force to the cycle number N are shown as Figure 1, where![]() . It shows that, with the eccentricity, the stroke and the stroke frequency of the inner cylinder being given as constants, as the flow behavior index n increases, the peak values (or valley values) of the tangential force Fz change a lot.
. It shows that, with the eccentricity, the stroke and the stroke frequency of the inner cylinder being given as constants, as the flow behavior index n increases, the peak values (or valley values) of the tangential force Fz change a lot.
Under different eccentricities e, the curves of the tangential force to the cycle number are shown as Figure 2. It shows that, with the flow behavior index n, the stroke S and the stroke frequency of the inner cylinder f being given as constants, as the eccentricity e increases, the peak values (or valley values) of the tangential force Fz change a lot.
Under different strokes S, the curves of the tangential force to the cycle number are shown as Figure 3. It shows that, with the flow behavior index n, the eccentricity e and the stroke frequency of the inner cylinder f being given as constants, as the strokes S increases, the peak values (or valley values) of the tangential force Fz change a lot.
![]()
Figure 1. The curves of the distribution of the tangential force of the HPAM aqueous solution under different flow behavior index (ρ = 998 Kg/m3, k = 10.886 × 10−2 Pa∙sn, e = 0.965 × 10−2 m, S = 1.0 m, f = 0.167 Hz).
![]()
Figure 2. The distribution of the tangential force of the HPAM aqueous solution of quality concentration 0.1% under different eccentricities (ρ = 998 Kg/m3, n = 0.556, k = 10.886 × 10−2 Pa∙sn, S = 1.0 m, f = 0.167 Hz).
![]()
Figure 3. The distribution of the tangential force of the HPAM aqueous solution of quality concentration 0.1% under different strokes (ρ = 998 Kg/m3, n = 0.556, k = 10.886 × 10−2 Pa∙sn, e = 0.965 × 10−2 m, f = 0.167 Hz).
Under different frequencies f, the curves of the tangential force distribution to the cycle number are shown as Figure 4. It shows that, with the flow behavior index n, the eccentricity e and the stroke S being given as constants, as the stroke frequency f increases, the peak values (or valley values) of the tangential force Fz change a lot.
5. Summary
1) Based on the governing equations of the inner cyinder of the unsteady flow of the power law fluid in eccentric annuli with the inner cylinder reciprocating axially in the bipolar coordinate system, the calculation formulae of tangential force on the wall of the inner cylinder of the power law fluid flowing in eccentric annuli with the inner cylinder reciprocating axially in the bipolar coordinate system were established, and the relevant numerical calculation method was given.
![]()
Figure 4. The distribution curves of tangential force of the HPAM aqueous solution of quality concentration 0.1% under different frequency (ρ = 998 Kg/m3, n = 0.556, k = 10.886 × 10−2 Pa∙sn, e = 0.965 × 10−2 m, S = 1.0 m).
2) Taking the HPAM aqueous solution for examples, by using the calculation formulae and method mentioned above, the tangential forces of the HPAM aqueous solution on the wall of the inner cylinder were calculated and the tangential force curves were plotted.
3) The effects on the tangential force of the flow behavior index of the power law fluid, the eccentricity of the eccentric annulus, the stroke and the stroke frequency of the inner cylinder were analyzed; the influence of the eccentricity was more obvious.