Erratum to “Improving the Power Generation Performance of a Solar Tower Using Thermal Updraft Wind” [Energy and Power Engineering Vol. 6 No. 11 (October 2014) 362-370] ()
5.2.2. Influence of the Wind Turbine on the Velocity
Figure 9 shows the relationship between the flow temperature and vertical velocity at 0.05 m above the rotor when it is rotating. Installing the wind turbine creates a resistance. The wind velocity decreases in comparison with the case with no wind turbine. In addition, the vertical wind velocity inside the diffuser tower is 1.4 times greater than that inside the cylindrical tower, i.e. 1) By installing the wind turbine, 2.6 m/s wind velocity (tem- perature difference 30˚K, diffuser type) was slowed down to 2.2 - 2.3 m/s (Figure 9) whereas the velocity was slightly slowed down to 1.3 m/s in the case with no wind turbine (temperature difference 38˚K, cylindrical type). 2) Even if a wind turbine was installed, the ratio between the velocity of the diffuser and cylindrical towers was about 1.4, which is almost the same ratio with or without the wind turbine. As a consequence, the velocities for the diffuser and cylindrical towers are clearly different.
5.2.3. Performance of Power Generation
Next we discuss the power. Figure 10 shows the turbine rotation speed for the diffuser tower was greater than
![]()
Figure 10. Temperature difference vs. rotation speed.
that for the cylindrical tower. We measured the speed of rotation of the rotor with a revolution counter. The increasing speed of rotation of the rotor relates directly to the power output. Here, we define power as P, Torque as Tr and number of rotation ω, the relationship is given by Equation (4):
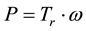 . (4)
. (4)
The power output is expected to increase for the diffuser tower. Figure 11 shows the power output vs. temperature difference. From the results in Figure 11, whereas the ratio of velocity between the diffuser and cylindrical towers is 1.4, the power output for the diffuser tower turns out to be 4 times greater than that for the cylindrical tower. This is because the power output is proportional to the cube of the velocity.
In addition, from the relationship of the output for the diffuser vs. flow temperature, the diffuser output produces power from a lower temperature difference than the cylindrical output. In using the diffuser shape tower for a solar tower, the wind velocity exceeds that for a cylindrical type tower.
Furthermore, even if a wind turbine is installed, the ratio of the speed increase is constant, the speed of rotation of the rotor increases and the power output increases considerably.
6. Conclusions
The purpose of this research is to focus on the shape of the solar tower, and increase the power output by changing the structure from the conventional cylindrical tower to a diffuser type tower, thus increasing the power output.
As a result of previous preliminary experiments conducted by Okada, the mini-model of a diffuser type tower achieved greater wind velocity than a cylindrical tower. In these experiments, we made the size of the model 5 times larger than the mini-model. By installing a wind turbine, we actually measured the obtained power output and verified it.
1) Initially, similar to the mini-model, we measured the wind velocity of the diffuser and cylindrical towers without a wind turbine. As the result, the wind velocity for the diffuser tower was greater than that for the cylindrical tower by a factor of 1.5 - 1.8 times. The velocity of this model was almost √5 times greater than that for the mini-model. A scaling law was established for the solar tower.
2) Next, by installing a wind turbine, the change in velocity and power output was measured. The ratio of velocity between the diffuser and cylindrical towers was almost 1.4 - 1.5, similar to the case for the temperature difference Δθ without a wind turbine. Because the power output was proportional to the cube of the velocity, the power output obtained in the diffuser tower was 4 times greater than that for the cylindrical tower.
From these results, we concluded that the diffuser tower, which had the advantage of a larger power output than the cylindrical tower, was the preferred option for a solar tower.
NOTES
*Corresponding author.