Ultrasonic Rangefinder Spikes Rejection Using Discrete Wavelet Transform: Application to UAV ()
1. Introduction
The field of aerial robotics has evolved in the past decades due to the rapid advances in sensors, computing and other technologies. These advances have increased the scope for commercial use of unmanned aerial vehicles (UAV). One specific UAV has been widely used as a research platform worldwide, the quadrotor. When equipped with appropriate sensors and control algorithms, they have the potential to provide cost-effective solutions to many indoor and outdoor applications. Their main advantage over other types of UAVs is its simple mechanical structure and fast dynamics that allow them to perform aggressive maneuvers. However, to autonomously control the quadrotor, its fast dynamics requires accurate and frequently updated knowledge about its attitude, velocity and position. Such knowledge can be provided by an inertial navigation system (INS). However, commercially available high quality ones are rather expensive, which motivate the development of navigation systems for quadrotors using low cost sensors. To measure the quadrotor’s position, Global Navigation Satellite System (GNSS) receivers, such as GPS, can be used outdoors, while vision based motion capture systems can be used in indoor applications. The drawback of using low GPS receivers is that they provide an accuracy of several meters, in addition to the attenuation and scattering of microwave signals in indoor environments which make them an unsuitable choice, whereas motion capture systems can be used only indoors, in addition to being rather expensive. Quadrotor platforms typically utilize barometric pressure sensors or ultrasonic range-finders to measure the altitude relative to the ground. Ultrasonic rangefinders have an advantage over the pressure sensors when the quadrotor is in the vicinity of the ground, therefore they are suitable for indoor applications. It is well known in practice that ultrasonic rangefinders suffer from spikes in distance measurements due to specular reflectance and acoustic noise. The presence of these spikes is problematic since the distance measurements are used as the feedback to the altitude control system responsible for holding the altitude of the quadrotor in 3D space.
Due to its short time span, the analysis of the altitude measurement spikes requires resolution in time and frequency instead of frequency alone. Therefore, the wavelet transform is a suitable choice for analyzing the signal. The wavelet transform has an advantage over the Fourier transform in its ability to produce temporal resolution i.e., it captures both location in time information and frequency information. Therefore, it has been a suitable candidate for applications in numerical fields [1] . Sheybani et al. [2] have utilized the wavelet transform to filter diagnostic data signals with spikes and noise to remove the spikes in the signals while preserving the noise. The wavelet transform has been also used in [3] to filter spikes in power converter systems. Moreover, the wavelet transform has been used in image processing applications as in [4] , generating the low-pass image using an approach based on DWT .Wavelet theory has been applied successfully to a number of biomedical problems. Uebeyli et al. [5] apply the wavelet transform to extract features from the spike-wave discharges record of rats, while wavelet transform has been used in [6] to analyze physiological data such as heart rhythm, chest volume, and blood oxygen saturation.
In this paper, an efficient method to remove measurement spikes from the ultrasonic sensor will be presented such that the control system is unaffected by the spikes. The methodology is based on the wavelet transform of the ultrasonic measurement signal. The spikes rejection algorithm is then implemented in simulation to study the effect on the control performance of a hovering quadrotor. Then, the algorithm is implemented digitally on a data set of ultrasonic measurements from a real flight. The paper is organized as follows. Section 2 discusses the dynamical model of the quadrotor UAV, both the nonlinear and linearized models. Section 3 presents the linear altitude controller while Section 4 includes the discrete wavelet transform based methodology used to filter the spikes in the ultrasonic measurements. Sections 5 and 6 include the simulation and experimental results respectively and finally Section 7 discusses the conclusions of this work.
2. Dynamical Model and Controller Design
The equations of motion of quadrotors have been derived and analyzed by several researchers in the literature [7] [8] . The quadrotor’s dynamic equations of motion (EoM) are summarized in the following equations
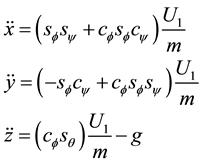 (1)
(1)
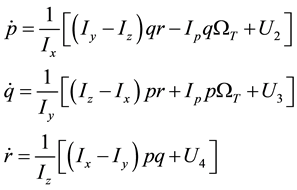 (2)
(2)
where x, y and z are the position of the quadrotor’s center of mass; ϕ, θ, ψ are the Z-Y-X Euler angles which are used to represent the orientation of the body-fixed frame with respect to the inertial frame; p, q and r are the body angular rates; m is the quadrotor’s mass while Ix, Iy, Iz are the quadrotor’s mass moment of inertia components represented in the body-fixed frame; Ip is the propeller's mass moment of inertia with respect to the propeller-fixed frame while ΩT is the sum of the four propeller angular velocities. The terms U1, U2, U3 and U4 are
the collective thrust, roll, pitch and yaw forces generated by the four propellers. Finally 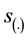 and
and  are short hand notations for
are short hand notations for 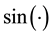 and
and 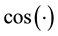 respectively.
respectively.
For the hovering configuration of the quadrotor, we can make small angle assumptions, neglect higher order terms and define new control inputs which will result in a linearized model. The translational and rotational EoM after linearization about the hovering configuration will be written as
 (3)
(3)
where Ωh represents the hovering speed of the propellers, l, b, d are the distance from the rotors to the CoM, thrust and drag factors respectively, while  are the deviations in collective thrust, roll, pitch and yaw forces respectively which represent the new control inputs. The four decoupled subsystems of the altitude, roll, pitch and yaw axes represented in the Laplace domain can be written as
are the deviations in collective thrust, roll, pitch and yaw forces respectively which represent the new control inputs. The four decoupled subsystems of the altitude, roll, pitch and yaw axes represented in the Laplace domain can be written as
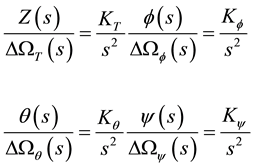 (4)
(4)
where  are constants including the system parameters in the linearized equations of motion while s is the Laplace variable. Incorporating all the system parameters in its transfer function was due to the choice of the modified control inputs. This modification decreases the sensitivity of the control performance to the system parameters due to the action of feedback which increases the robustness of the designed control system to errors in the parameter identification process.
are constants including the system parameters in the linearized equations of motion while s is the Laplace variable. Incorporating all the system parameters in its transfer function was due to the choice of the modified control inputs. This modification decreases the sensitivity of the control performance to the system parameters due to the action of feedback which increases the robustness of the designed control system to errors in the parameter identification process.
Classical proportional, integral and derivative (PID) control has been exploited by several researchers in [9] - [11] and has been able to successfully stabilize the quadrotor in its hovering position. It has the advantage that it is model independent and is simple to implement. The altitude controller will be chosen to be a PID controller with the derivative action on the feedback action only (Figure 1) to avoid spikes in the control signal [12] . The controller transfer functions C(s) and H(s) are given by
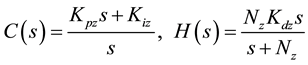 (5)
(5)
where  are the proportional, integral and derivative controller gains respectively, while
are the proportional, integral and derivative controller gains respectively, while 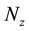 is the low pass filter coefficient.
is the low pass filter coefficient.
3. Discrete Wavelet Transform
To detect and remove these spikes a DWT approach was followed. The DWT decomposes the ultrasonic mea-
![]()
Figure 1. Altitude axis block diagram with PID controller with the derivative action on the feedback signal.
surement signal into two sets of coefficients known as detail coefficients and approximate coefficients. The signal can be reconstructed from these same coefficients using the inverse DWT after detecting and removing the spikes as illustrated in Figure 2. The signal decomposition is performed by passing the signal through a low pass filter Hd(z) and a high pass filter Gd(z) [3] . The two filters are a pair of quadrature mirror filters related with the power complement property given by
 (6)
(6)
which indicates that the sum of the square of the frequency response magnitude for both filters should be equal to one for all frequencies . The Haar Wavelet is chosen as the mother wavelet since it can be implemented using the first order Finite Impulse Response (FIR) filters given in the Z domain by
. The Haar Wavelet is chosen as the mother wavelet since it can be implemented using the first order Finite Impulse Response (FIR) filters given in the Z domain by
![]() (7)
(7)
The approximate and the detail coefficients are produced from the low pass and high pass filters respectively, after a dyadic down sampling which keeps even indexed elements only. A threshold procedure is applied to the approximate and detail coefficients and then the despiked signal is reconstructed using the inverse DWT. The Haar low pass and high pass FIR filters used in the reconstruction phase are given by
![]() (8)
(8)
In this work, spikes are removed from the original signal by setting the detail coefficients to zero over the period when the threshold is exceeded. The approximate coefficients are also modified in regions where the difference between two consecutive coefficients exceeds a certain threshold. The approximate coefficients are then set to the previous value in the case of spikes detection. This modification of the approximate coefficients was not performed in [3] as a three level decomposition of the input signal was performed. However, in the approach followed in this work, only a single level decomposition was needed which reduced the time delay between the input signal and the filtered measurement. To avoid implementation issues that may arise, the modification of the approximate coefficients is only performed consecutively for a specified time window.
4. Simulation Results
To study the effect of these spikes on the control performance, a simulation study was performed by a developed simulation environment using MATLAB. The results of this simulation run can be seen in figures (Figure 3 and Figure 4). In the simulation, two spikes were intentionally added to the measurements at t = 5 s and t = 12 s. The faulty measurements have caused spikes in the control signal resulting in its saturation which in return caused a large overshoot in the quadrotor’s altitude. To validate the developed algorithm, the DWT-based algorithm was implemented in the simulation environment. The simulation environment was modified to include the
![]()
Figure 2. Discrete wavelet transform architecture. The superscript * denotes signals before removing spikes.
![]()
Figure 3. Simulation results: spikes in the ultrasonic measurements.
![]()
Figure 4. Simulation results: quadrotor’s altitude (upper) and control signal (lower) in the presence of spikes in the ultrasonic measurements.
algorithm implemented digitally with a sampling frequency of 100 Hz. A simulation run was performed to show the result after applying the spikes removal algorithm which is shown in figures (Figure 5 and Figure 6). The results indicate that after applying the DWT-based algorithm, the ultrasonic measurements were corrected and the performance was unaffected by the spikes in the measurements.
5. Experimental Validation
After testing the algorithm in the simulation environment, it was implemented on the quadrotor platform. The
![]()
Figure 5. Simulation results: quadrotor’s altitude (upper) and control signal (lower) after applying the DWT-based algorithm.
![]()
Figure 6. Simulation results: spikes removed from the ultrasonic measurements. Figure shows the raw signal (dashed blue) and the signal after removing the spikes (solid red).
experiment was performed by gathering ultrasonic measurements from a real sensor mounted on-board a quadrotor platform developed in the Control and Dynamics Lab in the German University in Cairo. The quadrotor system developed consists of four brushless DC motors driven by Electronic Speed Controllers (ESCs) on board. The quadrotor is equipped with various sensors including an Inertial Measurement Unit (IMU) which consists of an accelerometer and gyroscope triad. Moreover, the quadrotor contains a three-axis magnetometer and an optical flow sensor (PX4FLOW Smart Camera Manufactured by Pixhawk) which includes also an ultrasonic range finder. The quadrotor is equipped with an Arduino Due micro-controller responsible for processing incoming data from the sensors and commanding desired rotor speed to the ESCs. Moreover, a Raspberry Pi (RPI) computer is installed on the quadrotor platform which is responsible for the implementation of the control algorithms, communicating with the Arduino Due on board in addition to communicating with the ground station control software developed.
In the performed experiment, the quadrotor control system was responsible for stabilizing the quadrotor’s attitude only and the quadrotor was free to move vertically with manual assistance that prevents it from falling to the ground. Figure 7 shows a typical ultrasonic measurement data set with significant spikes. The approximate and detail coefficients single level DWT of this signal are shown as well. The experiment was performed for 18 seconds with a total of 360 samples which implies that the sampling frequency is 20 Hz which is the typical frequency for ultrasonic rangefinders. Due to the dyadic down-sampling, the number of the approximate and detail coefficients for this signal is 180 for each. The threshold is then applied to these coefficients and finally the despiked signal is reconstructed from the modified coefficients by the inverse DWT as shown in Figure 8. The flowchart for the algorithm implemented on the RPI computer is shown in Figure 9.
![]()
Figure 7. Experimental results: applying DWT on ultrasonic measurement (upper) with approximate coefficients (middle) and detail coefficients (lower).
![]()
Figure 8. Experimental results: spikes rejection results: distance measurements.
6. Conclusion
In this paper, a discrete wavelet transform based algorithm for removing spikes in ultrasonic range finder measurements has been presented. The ultrasonic rangefinder was utilized by a quadrotor UAV to provide altitude measurements for the altitude controller responsible for stabilizing the quadrotor. A simulation environment was developed using the quadrotor’s dynamical model and the effect of spikes on the stabilization performance was studied. The spikes rejection algorithm was then implemented in the simulation environment and a comparison between the hovering performance with and without the algorithm was presented. The results had shown that using the algorithm, the controller was unaffected by the spikes in the measurements. Finally, the algorithm was implemented digitally on ultrasonic measurements from a real flight experiment. One major advantage of the developed algorithm was that it didn’t require any iteration within the sampling period, therefore it was computa-
![]()
Figure 9. Flowchart of spikes removing algorithm implemented on RPI.
tionally inexpensive. This advantage is due to the choice of the Haar wavelet which can be implemented using first order FIR filters.