Degree Splitting of Root Square Mean Graphs

S. S. Sandhya¹, S. Somasundaram², S. Anusa³

¹Department of Mathematics, Sree Ayyappa College for Women, Chunkankadai, India.
²Department of Mathematics, Manonmaniam Sundaranar University, Tirunelveli, India.
³Department of Mathematics, Arunachala College of Engineering for Women, Vellichanthai, India.

DOI: 10.4236/am.2015.66086                

Abstract

Let be an injective function. For a vertex labeling f, the induced edge labeling is defined by, or ; then, the edge labels are distinct and are from . Then f is called a root square mean labeling of G. In this paper, we prove root square mean labeling of some degree splitting graphs.

Keywords

Graph, Path, Cycle, Degree Splitting Graphs, Root Square Mean Graphs, Union of Graphs

1. Introduction

The graphs considered here are simple, finite and undirected. Let denote the vertex set and 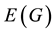denote the edge set of G. For detailed survey of graph labeling we refer to Gallian [1] . For all other standard terminology and notations we follow Harary [2] . The concept of mean labeling on degree splitting graph was introduced in [3] . Motivated by the authors we study the root square mean labeling on degree splitting graphs. Root square mean labeling was introduced in [4] and the root square mean labeling of some standard graphs was proved in [5] - [11] . The definitions and theorems are useful for our present study.

Definition 1.1: A graph 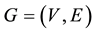with p vertices and q edge is called a root square mean graph if it is possible to label the vertices with distinct labels 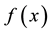from 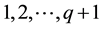in such a way that when

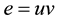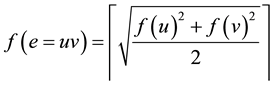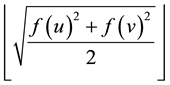each edge is labeled with or, then the edge

labels are distinct and are from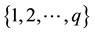. In this case f is called root square mean labeling of G.

Definition 1.2: A walk in which 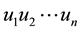are distinct is called a path. A path on n vertices is denoted by.

Definition 1.3: A closed path is called a cycle. A cycle on n vertices is denoted by.

Definition 1.4: Let be a graph with, where each is a set of vertices having at least two vertices and having the same degree and. The degree splitting graph of G is denoted by and is obtained from G by adding the vertices and joining to each vertex of The graph G and its degree splitting graph are given in Figure 1.

Definition 1.5: The union of two graphs and is a graph with vertex set and the edge set.

Theorem 1.6: Any path is a root square mean graph.

Theorem 1.7: Any cycle is a root square mean graph.

2. Main Results

Theorem 2.1: is a root square mean graph.

Proof: The graph is shown in Figure 2.

Let. Let the vertex set of G be where. Define a function by

Figure 1. The graph G and its degree splitting graph.

Figure 2. The graph.

Then the edges are labeled as

Then the edge labels are distinct and are from. Hence by definition 1.1, G is a root square mean graph.

Example 2.2: Root square mean labeling of is shown in Figure 3.

Theorem 2.3: is a root square mean graph.

Proof: The graph is shown in Figure 4.

Let. Let the vertex set of G be where. Define a function by

Figure 3. Root square mean labeling of.

Figure 4. The graph.

Then the edges are labeled as

Then the edge labels are distinct and are from. Hence by definition 1.1, G is a root square mean graph.

Example 2.4: Root square mean labeling of is shown in Figure 5.

Theorem 2.5: is a root square mean graph.

Proof: The graph is shown in Figure 6.

Let. Let the vertex set of G be where

. Define a function by

Figure 5. Root square mean labeling of.

Figure 6. The graph.

Then the edges are labeled as

Then the edge labels are distinct and are from. Hence by definition 1.1, G is a root square mean graph.

Example 2.6: The labeling pattern of is shown in Figure 7.

Theorem 2.7: is a root square mean graph.

Proof: The graph is shown in Figure 8.

Let. Let the vertex set of G be where

. Define a function by

Figure 7. The labeling pattern of.

Figure 8. The graph.

Then the edges are labeled as

Then the edge labels are distinct and are from. Hence by definition 1.1, G is a root square mean graph.

Example 2.8: The labeling pattern of is shown in Figure 9.

Theorem 2.9: is a root square mean graph.

Proof: The graph is shown in Figure 10.

Let. Let the vertex set of G be where

.

Define a function by

Then the edges are labeled as

Figure 9. The labeling pattern of.

Figure 10. The graph.

Then the edge labels are distinct and are from. Hence by definition 1.1, G is a root square mean graph.

Example 2.10: The root square mean labeling of is shown in Figure 11.

Theorem 2.11: is a root square mean graph.

Proof: The graph is shown in Figure 12.

Let. Let its vertex set be

where.

Define a function by

Figure 11. The root square mean labeling of.

Figure 12. The graph.

Then the edges are labeled as

Then the edge labels are distinct and are from. Hence by definition 1.1, G is a root square mean graph.

Example 2.12: The labeling pattern of is shown in Figure 13.

Theorem 2.13: is a root square mean graph.

Proof: The graph is shown in Figure 14.

Figure 13. The labeling pattern of.

Figure 14. The graph.

Let. Let its vertex set be

where.

Define a function by

Then the edges are labeled as

Then the edge labels are distinct and are from. Hence by definition 1.1, G is a root square mean graph.

Example 2.14: The labeling pattern of is shown in Figure 15.

Theorem 2.15: is a root square mean graph.

Proof: The graph is shown in Figure 16.

Let. Let its vertex set be

Figure 15. The labeling pattern of.

Figure 16. The graph.

where.

Define a function by

Then the edges are labeled as

Then the edge labels are distinct and are from. Hence by definition 1.1, G is a root square mean graph.

Figure 17. The root square mean labeling of.

Example 2.16: The root square mean labeling of is given in Figure 17.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Gallian, J.A. (2012) A Dynamic Survey of Graph Labeling. The Electronic Journal of Combinatories.
[2]	Harary, F. (1988) Graph Theory. Narosa Publishing House Reading, New Delhi.
[3]	Sandhya, S.S., Jayasekaran, C. and Raj, C.D. (2013) Harmonic Mean Labeling of Degree Splitting Graphs. Bulletin of Pure and Applied Sciences, 32E, 99-112.
[4]	Sandhya, S.S., Somasundaram, S. and Anusa, S. (2014) Root Square Mean Labeling of Graphs. International Journal of Contemporary Mathematical Sciences, 9, 667-676.
[5]	Sandhya, S.S., Somasundaram, S. and Anusa, S. (2015) Some More Results on Root Square Mean Graphs. Journal of Mathematics Research, 7.
[6]	Sandhya, S.S., Somasundaram, S. and Anusa, S. (2014) Root Square Mean Labeling of Some New Disconnected Graphs. International Journal of Mathematics Trends and Technology, 15, 85-92. http://dx.doi.org/10.14445/22315373/IJMTT-V15P511
[7]	Sandhya, S.S., Somasundaram, S. and Anusa, S. (2014) Root Square Mean Labeling of Subdivision of Some More Graphs. International Journal of Mathematics Research, 6, 253-266.
[8]	Sandhya, S.S., Somasundaram, S. and Anusa, S. (2014) Some New Results on Root Square Mean Labeling. International Journal of Mathematical Archive, 5, 130-135.
[9]	Sandhya, S.S., Somasundaram, S. and Anusa, S. (2015) Root Square Mean Labeling of Subdivision of Some Graphs. Global Journal of Theoretical and Applied Mathematics Sciences, 5, 1-11.
[10]	Sandhya, S.S., Somasundaram, S. and Anusa, S. (2015) Root Square Mean Labeling of Some More Disconnected Graphs. International Mathematical Forum, 10, 25-34.
[11]	Sandhya, S.S., Somasundaram, S. and Anusa, S. (2015) Some Results on Root Square Mean Graphs. Communicated to Journal of Scientific Research.