Study of the Convergence of the Increments of Gaussian Process

Abdelkader Bahram¹, Shaban A. El-Shehawy²

¹Department of Mathematics, Djillali Liabes University, Sidi Bel Abbès, Algeria.
²Department of Mathematics, Faculty of Science, Menoufia University, Shebin El-Kom, Egypt.

DOI: 10.4236/am.2015.66085                

Abstract

Let be a Gaussian process with stationary increments . Let be a nondecreasing function of t with . This paper aims to study the almost sure behaviour of where

with and is an increasing sequence diverging to .

Keywords

Wiener Process, Gaussian Process, Law of the Iterated Logarithm, Regularly Varying Function

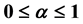with and 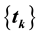is an increasing sequence diverging to.

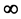Keywords:

1. Introduction

Let 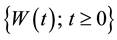be a standard Wiener process. Suppose that 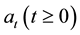is a nondecreasing function of t such that with 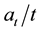is nonincreasing and 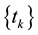is an increasing sequence diverging to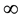. In [1] the following results are established.

i) If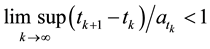, then

(1)

and

(2)

where and

.

ii) If, then

,

where, and.

In this paper the limit theorems on increments of a Wiener process due to [1] are developed to the case of a Gaussian process. This can be considered also as an extension of the results to Gaussian processes obtained in [2] . Throughout this paper, we shall always assume the following statements: Let be an almost

surely continuous Gaussian process with, and, where

is a function of. Further we assume that, , is a nondecreasing continuous concave, regularly varying function at exponent at (e.g., if is a standard Wiener pro- cess, then).

Let be a nondecreasing function of t with. For large t, let us denote

where and is an increasing function of.

We define two continuous parameter processes and by

and

.

2. Main Results

In this section we provide the following two theorems which are the main results. We concern here with the development of the limit theorems of a Wiener process to the case of a Gaussian process under consideration the above given assumptions.

Theorem 1. Let be a nondecreasing function of t where with the nonincreasing function and let be any increasing sequence diverging to such that

, (3)

then

(4)

and

(5)

where.

We note that for large k in case of the Wiener process. It is interesting to compare (1) and (2) with (4) and (5) respectively.

Theorem 2. Let be a nondecreasing function of where with the nonincreasing function and let be an increasing sequence diverging to such that

, (6)

then

(7)

and

(8)

where and.

3. Proofs

In order to prove Theorems 1 and 2, we need to give the following lemmas.

Lemma 1. (See [3] ). For any small there exists a positive depending on such that for all

,

where m is any large number and is defined above.

Lemma 2. (See [4] ) Let and be centered Gaussian processes such that

for all and for all. Then for any real number u

.

Proof of Theorem 1. Firstly, we prove that

(9)

For any with the condition (3), we define an increasing sequence by

.

For instance, let for some,

.

The condition (3) is satisfied, and for large k, and. By Lemma 1, we have, for any small,

(10)

where k is large enough and is a constant. By the definition of,.

We shall follow the similar proof process as in [5] . Set

.

Since is an increasing sequence, the fact that implies. Consider the odd subse-

quence of and define the sequence of events in the following form

.

By (10), for large k we have

where is a constant. From the fact, it is clear that

.

Since, we get. Also,

. (11)

Setting

and

,

we have

.

Let

,

and

.

Then, by (11) and the concavity of we find that

This implies that. Using Lemma 2, we obtain

where. It follows from the Borel-Cantelli lemma that

Also, the same result for the even subsequence of is easily obtained. Therefore we have (9).

To finish the proof of Theorem 1, we need to prove

(12)

The proof of (12) is similar to the provided proof in [1] . Thus the proof of Theorem 1 is complete.

Proof of Theorem 2. Firstly, we prove that

(13)

According to Lemma 1, we have

provided k is large enough, where and.

From the definition of, it follows that

.

Thus, (13) is immediate by using Borel Cantelli lemma.

To finish the proof of Theorem 2 we need to prove

(14)

Let

.

Using the well known probability inequality

(see [6] ), one can find positive constants C and K such that, for all,

where and. By the definition of, we have

.

The condition (6) implies that there exists such that for all. So, using Lemma 2 and the concavity of, we obtain

,

where and Borel-Cantelli lemma implies (14). If, then Theorem 2 is immediate. Thus the proof of Theorem 2 is complete.

4. Some Results for Partial Sums of Stationary Gaussian Sequence

In this section we obtain similar results as Theorems 1 and 2 for the case of partial sums of a stationary Gaussian sequence. Let be a stationary Gaussian sequence with, , and

for all We define with and set.

Assume that can be extended to a continuous function with which is nondecreasing and regularly varying with exponent at. Suppose that is a nondecreasing sequence of positive integers such that. For large n, we define

,

where and is an increasing function of n and also we define discrete time parameter processes by

and

,

respectively, where is an increasing sequence of positive integers diverging to. By the same way as in the proofs of Theorems 1 and 2, we obtain the following results.

Theorem 3. Under the above statements of, and, for we have the following:

i) If, then

ii) If, then

where

.

Example. Let be a fractional Brownian motion with the covariance function

. Then

.

Define random variables

,

and.

Then

and is a stationary Gaussian sequence with, and for all. So we have Theorem 3.

In particular if, then is an i.i.d. Gaussian sequence with and.

5. Conclusion

In this paper, we developed some limit theorems on increments of a Wiener process to the case of a Gaussian process. Moreover, we obtained similar results of these limit theorems for the case of partial sums of a stationary Gaussian sequence. Some obtained results can be considered as extensions of some previous given results to Gaussian processes.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Bahram, A. (2014) Convergence of the Increments of a Wiener Process. Acta Mathematica Universitatis Comenianae, 83, 113-118.
[2]	Hwang, K.S., Choi, Y.K. and Jung, J.S. (1997) On Superior Limits for the Increments of Gaussian Processes. Statistics and Probability Letters, 35, 289-296. http://dx.doi.org/10.1016/S0167-7152(97)00025-4
[3]	Choi, Y.K. (1991) Erdös-Réyi Type Laws Applied to Gaussian Process. Journal of Mathematics of Kyoto University, 31, 191-217.
[4]	Slepian, D. (1962) The One-Sided Barrier Problem for Gaussian Noise. Bell System Technical Journal, 41, 463-501. http://dx.doi.org/10.1002/j.1538-7305.1962.tb02419.x
[5]	Vasudeva, R. and Savitha, S. (1993) On the Increments of Weiner Process—A Look through Subsequences. Stochastic Processes and Their Applications, 47, 153-158. http://dx.doi.org/10.1016/0304-4149(93)90101-9
[6]	Fernique, X. (1975) Evaluations of Processus Gaussian Composes. Probability in Banach Spaces. Lecture Notes in Mathematics, 526, 67-83.