Synchronization of Impulsive Real and Complex Van der Pol Oscillators ()
1. Introduction
The stabilization and control of nonlinear systems is one of the most important properties of the systems and has been studied widely by many researchers in control theory (see Refs. [2] - [5] ). As the key technology of secure communication, chaotic synchronization has been widely developed since Pecora and Carroll [6] proposed the principle of chaos synchronization and realized it in the circuit in 1990. The basic behavior and chaotic synchronization have been studied by several researchers (see Refs. [7] - [10] ). The concept of synchronization consists in making two chaotic systems (identical or different) which oscillate in a synchronized manner.
On the other hand, since Fowler et al. [11] introduced the complex Lorenz equations as a generalization of the real Lorenz system, many chaotic complex systems have been proposed such as chaotic complex Lu and Chen [1] [4] [8] [12] , complex Van der Pol [1] , and references therein.
A wide variety of methods have been proposed and applied for the synchronization of chaotic systems which include, for example, active control, global synchronization, adaptive control, linear and nonlinear feedback and back stepping design (see Refs. [5] [6] [9] [10] [13] - [15] ) and references therein. The great interest in synchronization is not only due to the possibility of sending messages through chaotic systems for secure communication, but also due to applications in other fields, such as electrical and automation engineering, biology and chemistry. The synchronized systems usually consist of two parts: A transmitter of chaotic signals (master oscillator) and a receiver (slave oscillator). A chaotic signal generated by the master oscillator may be used as an input in the slave oscillator. After synchronization, the trajectory of the slave oscillator asymptotically approaches that of the master oscillator and the error signal is zero.
In applied sciences and engineering there are a lot of problems involving complex variables which are described by these complex systems. For example, in secure communications, doubling the number of variables or using complex variables (which means using higher dimensional chaotic systems) increases the content and security of the transmitted information and in many important fields of physics, engineering and computer science, such as laser physics, control, flow dynamics and liquid mixing, electronic circuits, secure communications and information sciences (see Refs. [11] [16] - [22] ).
Recently, impulsive control has been widely used to stabilize and synchronize chaotic systems (see Refs. [23] - [27] ). Its necessity and importance lie in that, in some cases, the system cannot be controlled by continuous control. For example, a government cannot change savings rates of its central bank every day. Additionally, impulsive control may give a more efficient method to deal with systems that cannot endure continuous disturbance. Furthermore, impulsive method can also greatly reduce the control cost.
The main ideas of these impulses are to use samples of the state variables of the master system at discrete moments and to synchronize the slave system discretely. Once the error system of the two coupled systems is asymptotically stable, they are said to be synchronized. Generally speaking, these impulses are samples of the state variables of the master system at current discrete moments to drive the slave system. However, we can also design a novel impulse using not only current instantaneous errors, but also the previous time instants of errors. By using such a technique, we can increase the impulse distances and reduce the control cost.
In this work both real and complex Van der Pol oscillators were introduced and shown to exhibit chaotic limit cycles (see Ref. [1] ). We use the impulsive control technique to achieve synchronization of both real and complex Van der Pol oscillators.
 (1)
(1)
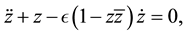 (2)
(2)
where 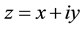 is a complex function with
is a complex function with , the par denotes the complex conjugate and
, the par denotes the complex conjugate and 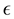 is a scalar parameter. If we select
is a scalar parameter. If we select 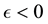 then both real and complex Van der Pol exhibit unstable limit cycles as shown in Figure 1. These systems arise in many important applications in physics, electronics, and biology. For more details, see Refs. [1] [28] - [30] ), and references therein.
then both real and complex Van der Pol exhibit unstable limit cycles as shown in Figure 1. These systems arise in many important applications in physics, electronics, and biology. For more details, see Refs. [1] [28] - [30] ), and references therein.
The rest of the paper is organized as follows: In Section 2, a theory on the stability of impulsive nonlinear equations is given. In Section 3, we apply the impulsive synchronization technique to study the chaos synchronization of real Van der Pol oscillator. In Section 4, we extend this investigation to complex Van der Pol oscillator in a chaotic state by using the same technique of Section 3. A good agreement is found between the analytical results and the numerical ones. Section 5 is devoted to the conclusions of this study.
2. Impulsive Control of Nonlinear System
The impulsive differential equations, that is, differential equations involving impulse effects, appear as a natural description of observed evolution phenomena of several real world problems, for example, that many biological phenomena involving thresholds, bursting rhythm models in medicine and biology, optimal control models in
economics, population dynamics see Refs. [11] [16] - [22] ). The mathematical description of these impulsive systems of differential equations are usually define as an ordinary differential equations coupled with a system of difference equations, as expressed in the following system:
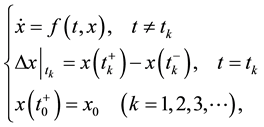 (3)
(3)
where 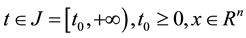 is the state variable, and
is the state variable, and 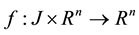 is a continuous-valued func-
is a continuous-valued func-
tion. The impulsive control law of system (3) is given by the sequence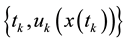 , which has the effect of
, which has the effect of
suddenly changing the state of the system at the instants![]() , where
, where ![]() and
and![]() . The difference equations are given by
. The difference equations are given by
![]() (4)
(4)
where ![]() and
and![]() . For simplicity, we assume that
. For simplicity, we assume that ![]() and
and
![]() can be chosen as
can be chosen as ![]() where
where ![]() being
being ![]() matrices. The objective is to find some (sufficient) conditions on the constant control gains,
matrices. The objective is to find some (sufficient) conditions on the constant control gains, ![]() , and the impulsive intervals
, and the impulsive intervals ![]() , such that the impulsively controlled system (3) is stable.
, such that the impulsively controlled system (3) is stable.
The above chaotic system can be written into the form
![]() (5)
(5)
where A is the linear part matrix of the corresponding system, and ![]() is the nonlinear part. We consider the system (5) as the master or drive system.
is the nonlinear part. We consider the system (5) as the master or drive system.
We consider the following chaotic system described by the dynamics
![]() (6)
(6)
as the slave or response system. If we define the synchronization error as
![]() (7)
(7)
then the error dynamics system of the impulsive synchronization is obtained as
![]() (8)
(8)
where![]() . We assume that the parameters of the master and slave systems are known and that the states of both systems (5) and (6) are available for measurement. Note that there exists a positive constant M for the chaotic systems (1) and (2) that
. We assume that the parameters of the master and slave systems are known and that the states of both systems (5) and (6) are available for measurement. Note that there exists a positive constant M for the chaotic systems (1) and (2) that ![]() for all t. For convenience, define the following notations:
for all t. For convenience, define the following notations:
![]()
The impulsive synchronization calculations lead to the following Theorem.
Theorem: If we consider the Lyapunov function defined by ![]() and
and
(I) If![]() , (
, (![]() is a constant) and there exist a constant
is a constant) and there exist a constant![]() , such that
, such that
![]() Then the trivial solution of system (8) is globally exponentially stable, that is, system (6) is globally exponentially synchronous with system (5).
Then the trivial solution of system (8) is globally exponentially stable, that is, system (6) is globally exponentially synchronous with system (5).
(II) If ![]() (
(![]() is a constant) and there exist a constant
is a constant) and there exist a constant![]() , such that
, such that
![]() Then system (6) is globally exponentially synchronous with system (5).
Then system (6) is globally exponentially synchronous with system (5).
In the following, we will takes real and complex Van der Pol oscillators for examples to obtain some more practical results.
3. Chaos Synchronization of Two Identical Real Van der Pol Oscillators
Assume that, the system (1) has two identical chaotic Van der Pol oscillators playing the master and slave oscillators respectively. The master oscillator is described as:
![]() (9)
(9)
and the slave oscillator is given by:
![]() (10)
(10)
where dots denote differentiation with respect to time, ![]() denotes the state vector of the master oscillator,
denotes the state vector of the master oscillator, ![]() denotes the state vector of the slave oscillator.
denotes the state vector of the slave oscillator.
Substituting![]() ,
, ![]() in (9) and
in (9) and![]() ,
, ![]() in (10) the resulting two systems of first order ODEs are:
in (10) the resulting two systems of first order ODEs are:
![]() (11)
(11)
![]()
and
![]() (12)
(12)
![]()
We wish to obtain an appropriate impulsive synchronization such that the solution of the slave oscillator asymptotically approaches the solution of the master oscillator, hereby, the two oscillators are synchronized with each other. To do that let us consider the error equation:
![]()
According to the synchronization theory the subtraction of Equation (12) from Equation (11) now gives:
![]() (13)
(13)
![]()
We can rewrite the above systems into the matrix form
![]() (14)
(14)
Then the error system of the impulsive synchronization is given by
![]() (15)
(15)
where ![]() is the linear part matrix of the corresponding system,
is the linear part matrix of the corresponding system,
![]() and
and ![]() denotes the instant when impulsive control occurs.
denotes the instant when impulsive control occurs.
System (13) can be considered as a control problem, which is a function of the error vector ![]() Also it is synchronized with respect to a Lyapunov function
Also it is synchronized with respect to a Lyapunov function ![]() via the design of Impulsive control, so one can achieve synchronization between the master and the slave oscillators.
via the design of Impulsive control, so one can achieve synchronization between the master and the slave oscillators.
Let us consider the Lyapunov function![]() . For
. For![]() , we have
, we have
![]() (16)
(16)
where![]() .
.
Corollary 1. Assume that ![]() and matrices
and matrices ![]()
I) If ![]() and there exists a constant
and there exists a constant![]() , such that
, such that ![]() then the system (12) is globally exponentially synchronous with system (11).
then the system (12) is globally exponentially synchronous with system (11).
II) If ![]() (
(![]() is a constant) and there exist a constant
is a constant) and there exist a constant![]() , such that
, such that ![]() , then system (12) is globally exponentially synchronous with system (11).
, then system (12) is globally exponentially synchronous with system (11).
According to Equation (16), the fixed point of system (13) is asymptotically stable, which means that the errors ![]() vanish as t goes to infinity.
vanish as t goes to infinity.
Systems (11) and (12) with (13) are solved numerically using Scilab software and the simulation results are shown in Figure 2 for ![]()
![]()
![]() and
and ![]()
![]() The eigenvalues are 0, −0.36. Then
The eigenvalues are 0, −0.36. Then![]() . If we choose
. If we choose![]() , then
, then
![]() . In the synchronization of two real systems, the initial conditions for the
. In the synchronization of two real systems, the initial conditions for the
drive and response systems are chosen as ![]() and
and![]() . We can get from the simulation that the approximate bounds
. We can get from the simulation that the approximate bounds ![]() of system (15) is 3. Thus
of system (15) is 3. Thus![]() . Take
. Take![]() , thus if
, thus if
![]() , when
, when ![]() system (11) is globally asymptotically synchronous with system (12).
system (11) is globally asymptotically synchronous with system (12).
Impulsive Synchronization of the Complex Van der Pol Oscillators
We study the impulsive synchronization of the complex Van der Pol oscillator. For simplifying the the problem,
![]()
Figure 2. Left figures (a) x1 versus y1, (b) x2 versus y2, (c) error e1 versus e2, impulsively synchronization of the real Van der Pol oscillator (1) cannot be stabilized with τ = 0.85; right figures (d) x1 versus y1, (e) x2 versus y2, (f) error e1 versus e2. Synchronization errors solutions of systems (1) and (13) with τ = 0.75.
we assume that we have two identical complex Van der Pol oscillator and using the same technique of sub- section 2. Oscillator (2) is a system of two coupled nonlinear Van der Pol oscillators that takes the form
![]() (17)
(17)
![]()
Let ![]()
![]()
![]() and
and![]() , then system (12) becomes:
, then system (12) becomes:
![]() (18)
(18)
![]()
![]()
![]()
which represent the master oscillator, so the slave oscillator is given by:
![]() (19)
(19)
![]()
![]()
![]()
let ![]() and
and ![]() denote the state vectors of master and slave oscillators respec- tively and T denotes the transpose. In order to apply the impulsive synchronization, we define the error
denote the state vectors of master and slave oscillators respec- tively and T denotes the transpose. In order to apply the impulsive synchronization, we define the error ![]() vector as:
vector as:
![]() (20)
(20)
The subtraction of system (18) from (19) gives a function of error vector ![]() as follows:
as follows:
![]() (21)
(21)
![]()
![]()
![]()
We can rewrite the error systems into the matrix form
![]() (22)
(22)
Then the error system of the impulsive synchronization is given by
![]() (23)
(23)
where
![]()
is the linear part matrix of the corresponding system and
![]()
Let us consider the Lyapunov function![]() . For
. For![]() , we have
, we have
![]() (24)
(24)
where![]() .
.
Corollary 2. Assume that ![]() and matrices
and matrices ![]()
I) If ![]() and there exists a constant
and there exists a constant![]() , such that
, such that![]() , then the sys- tem (19) is globally exponentially synchronous with system (18).
, then the sys- tem (19) is globally exponentially synchronous with system (18).
II) If ![]() (
(![]() is a constant) and there exist a constant
is a constant) and there exist a constant![]() , such that
, such that ![]() , then system (19) is globally exponentially synchronous with system (18).
, then system (19) is globally exponentially synchronous with system (18).
If ![]() then
then ![]() is negative and the system (21) is asymptotically stable which mean the error
is negative and the system (21) is asymptotically stable which mean the error ![]() ap- proaches zero as t approaches infinity.
ap- proaches zero as t approaches infinity.
Systems (18) and (19) with (21) are solved numerically using Scilab software and the simulation results are shown in Figure 3 for ![]()
![]()
![]() and
and ![]()
![]() The eigenvalues are 0, −0.18. Then
The eigenvalues are 0, −0.18. Then![]() . If we choose
. If we choose ![]() , then
, then
![]()
Figure 3. Left figures (a) x1 versus y1, (b) x2 versus y2, (c) x3 versus y3, impulsively synchronization of the complex Van der Pol oscillator (2) cannot be stabilized with τ = 0.85; right figures (a1) x1 versus y1, (b1) x2 versus y2, (c1) x3 versus y3 impulsively synchronization of the complex Van der Pol oscillator (2) can be stabilized with with τ = 0.75.
![]()
Figure 4. Synchronization errors solutions of system (21) cannot be stabilized with with τ = 0.85; (e), (f) and can be stabilized with τ = 0.75; (e1), (f1).
![]() . In the synchronization of two real systems, the initial
. In the synchronization of two real systems, the initial
conditions for the drive and response systems are chosen as ![]() and
and![]() . We can get from the simulation that the approximate bounds
. We can get from the simulation that the approximate bounds ![]() of system (23) is 3. Thus
of system (23) is 3. Thus
![]() . Take
. Take![]() , thus if
, thus if![]() , when
, when ![]() system (18)
system (18)
is globally asymptotically synchronous with system (19). Synchronization errors solutions of systems (21) are shown in Figure 4.
4. Conclusion
In this paper, we have applied an impulsive control technique for both real and complex Van der Pol oscillators to synchronize the chaotic limit cycles. This technique is widely used in the control of chaotic dynamical systems. The simulation results illustrate that, the trajectory of the slave system of both real and complex oscillators asymptotically approaches its analog of the master system, and finally the two systems implement their mutual synchronization.
Acknowledgements
We are very grateful to to all members of Applied mathematics Group (Department of Mathematics, Faculty of science, King Khalid University, KSA) for useful discussions on the topics investigated in this paper.
NOTES
*Corresponding author.