Starting with the original sub-quantum dark energy model, the current accelerating phase of the evolution of the universe is considered by constructing most economical cosmic models that use just general relativity and some dominating quantum effects associated with the probabilistic description of quantum physics. Two of such models are explicitly considered. They support an interpretation of dark energy in terms of the entangled energy of the universe. The model only violates the dominant energy condition quantum mechanically, that is by an amount given by the entanglement energy density, and gives rise to an asymptotically anti-de Sitter wormhole that becomes an asymptotically flat wormhole in the classical limit. It is shown that for most cosmic solutions such a wormhole does not predict any big trip phenomenon when it accretes phantom like energy.
1. Introduction
For the time being, the concept of dark energy continues posing one of the biggest problems of all physics which, in spite of many attempts and theories intended to solve or at least ameliorate it, has hitherto not found a conclusive outcome. Among such attempts and tentative theories, without trying to be at all exhaustive, we may count [1] what has been dubbed as quintessence, a scalar-field theory satisfying a equation of state , with the parameter w being bounded in such a way that
, with the parameter w being bounded in such a way that , or its phantom-energy extension for which
, or its phantom-energy extension for which . Also very popular have been the socalled cosmic generalized Chaplygin gas theories, where the equation of state adopts quite a more exotic structure, or the tachyonic models for dark energy that describe suitable generalizations from the quintessential scalar fields. Besides some rather serious difficulties in trying to fix the observational data, all of the above theories appear to be artificial such as inflaton theories are within the inflationary paradigm. Quite fashionable have also become in the last few years some forms of modified gravity theories in which one does not include any vacuum field but changes instead the gravitational Lagrangian by adding some convenient extra terms that are able to match inflation for large values of the Ricci curvature and describe an accelerating behavior at the smallest curvatures. Certain of such theories are mathematically equivalent to the introduction of quintessence and phantom fields, but all of them suffer from the typical problems associated with having a non Hilbert-Einstein action and may violate some solar-system tests.
. Also very popular have been the socalled cosmic generalized Chaplygin gas theories, where the equation of state adopts quite a more exotic structure, or the tachyonic models for dark energy that describe suitable generalizations from the quintessential scalar fields. Besides some rather serious difficulties in trying to fix the observational data, all of the above theories appear to be artificial such as inflaton theories are within the inflationary paradigm. Quite fashionable have also become in the last few years some forms of modified gravity theories in which one does not include any vacuum field but changes instead the gravitational Lagrangian by adding some convenient extra terms that are able to match inflation for large values of the Ricci curvature and describe an accelerating behavior at the smallest curvatures. Certain of such theories are mathematically equivalent to the introduction of quintessence and phantom fields, but all of them suffer from the typical problems associated with having a non Hilbert-Einstein action and may violate some solar-system tests.
From the observational standpoint the rapidly accumulating data coming from supernova Ia luminosity distance measurements, quasar statistics determinations or studies of the fluctuations in the cosmic microwave background radiation seem all to imply a value for the parameter of the equation of state which becomes each time closer and closer to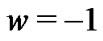 , which corresponds to a typical cosmological constant, with a certain ever stronger bias toward slightly smaller values. Thus, the realm where our accelerating universe appears to approximately lie on is one that can be expressed as a phantom-like small perturbation of the de Sitter space. Even though one could eventually accommodate the above dark energy and modified gravity models to account for such an observational scenario, that would ultimately appear rather unnatural. Moreover, none of such models can be shown to simultaneously satisfy the following two requirements, 1) exactly predicting what observational data point out in a natural way, and 2) an economic principle according to which one should not include unnecessary ingredients such as mysterious cosmic fluids or fields nor modifications of the very well tested background theories such as general relativity. The use of scalar fields in quintessence or k-essence scenarios is not with standing quite similar to including an inflaton in inflationary theories for the early universe [2]. Even though, owing to the success of the inflationary paradigm which actually shares its main characteristics with those of the present universal acceleration, many could take this similarity to be a reason enough to justify the presence of a scalar field also pervading the current universe, it could well be that a cosmic Occam’s Razor principle would turn out to be over and above the nice coincidence between predictions of usual models for inflation and what has been found in cosmic observations such as the measurement of background anisotropies. After all, the medieval opinion that the simplest explanation must be the correct explanation has proved to be extremely fruitful so far and, on the other hand, the paradigm of inflation by itself still raises some deep criticisms. Occam’s Razor is also against the idea of modifying gravity by adding to the relativistic Lagrangian some convenient extra terms.
, which corresponds to a typical cosmological constant, with a certain ever stronger bias toward slightly smaller values. Thus, the realm where our accelerating universe appears to approximately lie on is one that can be expressed as a phantom-like small perturbation of the de Sitter space. Even though one could eventually accommodate the above dark energy and modified gravity models to account for such an observational scenario, that would ultimately appear rather unnatural. Moreover, none of such models can be shown to simultaneously satisfy the following two requirements, 1) exactly predicting what observational data point out in a natural way, and 2) an economic principle according to which one should not include unnecessary ingredients such as mysterious cosmic fluids or fields nor modifications of the very well tested background theories such as general relativity. The use of scalar fields in quintessence or k-essence scenarios is not with standing quite similar to including an inflaton in inflationary theories for the early universe [2]. Even though, owing to the success of the inflationary paradigm which actually shares its main characteristics with those of the present universal acceleration, many could take this similarity to be a reason enough to justify the presence of a scalar field also pervading the current universe, it could well be that a cosmic Occam’s Razor principle would turn out to be over and above the nice coincidence between predictions of usual models for inflation and what has been found in cosmic observations such as the measurement of background anisotropies. After all, the medieval opinion that the simplest explanation must be the correct explanation has proved to be extremely fruitful so far and, on the other hand, the paradigm of inflation by itself still raises some deep criticisms. Occam’s Razor is also against the idea of modifying gravity by adding to the relativistic Lagrangian some convenient extra terms.
Besides general relativity, quantum theory is the other building block which can never be ignored while constructing a predicting model for any physical system. Although it is true that a quantum behavior must in general be expected to manifest for small-size systems, cosmology is providing us with situations where the opposite really holds. In fact, fashionable phantom models for the current universe are all characterized by an energy density which increases with time, making in this way the curvature larger as the size of the universe becomes greater. In such models quantum effects should be expected to more clearly manifest at the latest times where the universe becomes largest. Thus, it appears that quantum theory should necessarily be another ingredient in our task to build up an economical theory of current cosmology without contravening the Occam’s Razor philosophy.
A cosmological model satisfying all the above requirements has been recently advanced [3-6]. It was in fact constructed using just a gravitational Hilbert-instein action without any extra terms and taking into account the probabilistic quantum effects on the trajectories of the particles but not the dynamical properties of any cosmic field such as quintessence or k-essence. The resulting most interesting cosmic model describes an accelerating universe with an expansion rate that goes beyond that of the de Sitter universe into the phantom regime where the tracked parameter of the universal state equation becomes slightly less than –1, and the future is free from any singularity. Such a model, although still a toy one, will thus describe what may be dubbed a benigner phantom universe because, besides being regular along its entire evolution, it does not show the violent instabilities driven by a non-canonical scalar-field kinetic term as by construction the model does not have a negative kinetic term nor it classically violates the dominant energy condition which guarantees the stability of the theory, contrary to what the customary phantom models do. Another cosmic model was also obtained which describes an initially accelerating universe with equation of state parameter always greater than –1, that eventually becomes decelerating for a while, to finally contract down to a vanishing size asymptotically at infinity. The latter model seems to be less adjustable to current observational data although we are not completely sure as this is a toy model.
In the context of the dark energy models new phenomena can be predicted which appear to be extremely surprising. Thus, if the parameter of the equation of state w is less than –1, then space-time wormholes should take place as a rather natural ingredient of the cosmic theory because in this case the dominant energy condition (DEC) is violated. Under these circumstances the existing phantom energy would be accreted by the wormholes in such a way that the size of their throat quickly increases to eventually diverge even before the occurrence of the big rip singularity. The cosmic big trip [7-9] is a process thought to take eventually place in the far future by which naturally existing wormholes accrete phantom energy in such a way that they will end up engulfing the universe itself. The characteristics of this process have been many times reviewed and its main difficulties discussed, including: the static character of the used metrics, the asymptotic flatness of the wormhole space-times, the intrinsic quantum instability of the Cauchy (chronology) horizons and the violation of the holographic bounds on entropy and information. In this way, some criticisms have been raised against that process, mainly by Faraoni and Israel [10], Faraoni [11] and others [12]. However, all of such criticisms have been refuted [13] at the end of the day and therefore, in spite of the rather Dante’s infernal aspect of the phenomenon, the cosmic big trip still stands up as one of the potential ingredients of current cosmology and strongly menaces the future of the universe. In the present paper we shall consider the problem of dark energy accretion in the realm of the above mentioned benigner phantom like model. It will be seen that the effect of the quantum DEC violating term is to covert an asymptotically flat (e.g. Morris-Thorne) wormhole space-time into its asymptotically anti-de Sitter counter part, which does not give rise to any big trip phenomenon, but leads to a wormhole throat divergence at exactly the same time at which the big rip singularity takes place, in close accordance with the expected co-moving evolution [14].
2. Asymptotically Flat Space-Time Holes
One of the most interesting implications from the socalled benigner phantom and dark energy models respectively corresponding to the solutions  and
and  is the interpretation [6] that the potential energy density is nothing but the entanglement energy density of the universe, that is
is the interpretation [6] that the potential energy density is nothing but the entanglement energy density of the universe, that is , where
, where 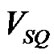 is the so-called sub-quantum potential density [3-6]. In what follows we shall use such an implication in all the calculations of the vacuum energy accretion that we will consider.
is the so-called sub-quantum potential density [3-6]. In what follows we shall use such an implication in all the calculations of the vacuum energy accretion that we will consider.
Thus, if we place a Schwarzschild black hole with initial mass  in the universe described by the suggested model for
in the universe described by the suggested model for , the mechanism advanced by Babichev, Dokuchaev and Eroshenko [15] would imply that the black hole will accrete this sub-quantum phantom energy so that it would progressively lose mass down to finally vanish at
, the mechanism advanced by Babichev, Dokuchaev and Eroshenko [15] would imply that the black hole will accrete this sub-quantum phantom energy so that it would progressively lose mass down to finally vanish at , according to the equation
, according to the equation
 (1)
(1)
With D a constant. If we place a Morris-Thorne wormhole with initial throat radius  instead, the corresponding accretion mechanism [7-9] leads now to a progressive increase of the wormhole size governed by
instead, the corresponding accretion mechanism [7-9] leads now to a progressive increase of the wormhole size governed by
 (2)
(2)
with 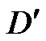 another constant, bringing us to consider the existence of a big trip process [7-9] by which, relative to an asymptotic observer at
another constant, bringing us to consider the existence of a big trip process [7-9] by which, relative to an asymptotic observer at , the wormhole will quickly grows up to engulf the universe itself, blowing up at a finite time in the future given by
, the wormhole will quickly grows up to engulf the universe itself, blowing up at a finite time in the future given by
 (3)
(3)
In this case, on times 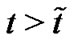 the wormhole converts into an Einstein-Rosen bridge which decays into a black hole plus a white hole that will in this case progressively lose mass to vanish at
the wormhole converts into an Einstein-Rosen bridge which decays into a black hole plus a white hole that will in this case progressively lose mass to vanish at  [7-9]. This result holds both for a static wormhole metric and when the throat radius is allowed to be time-dependent [7-9].
[7-9]. This result holds both for a static wormhole metric and when the throat radius is allowed to be time-dependent [7-9].
We shall now briefly consider solution . If
. If , then this solution corresponds to an initial period of accelerating expansion with an equation-of-state parameter w greater, though very close to –1. This situation would stand until a time
, then this solution corresponds to an initial period of accelerating expansion with an equation-of-state parameter w greater, though very close to –1. This situation would stand until a time
 (4)
(4)
which corresponds to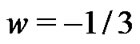 . After
. After  the universe would keep expanding but now in a decelerating way until a time
the universe would keep expanding but now in a decelerating way until a time
 (5)
(5)
After which the universe entered a contracting phase which would be maintained until . If
. If then the present model would no longer be valid. It could be at first sight thought that the universe might now be in the phase
then the present model would no longer be valid. It could be at first sight thought that the universe might now be in the phase  of solution
of solution , but current constraints on w [1] seem to preclude that it can be greater than –1. Besides thermodynamical considerations, perhaps another argument against solution
, but current constraints on w [1] seem to preclude that it can be greater than –1. Besides thermodynamical considerations, perhaps another argument against solution 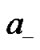 [3-6] be the fact that for this kind of solution, while the accretion of the sub-quantum energy onto a Morris-Thorne wormhole leads to a progressive decrease of the wormhole size according to the law
[3-6] be the fact that for this kind of solution, while the accretion of the sub-quantum energy onto a Morris-Thorne wormhole leads to a progressive decrease of the wormhole size according to the law , the size of a black hole of initial mass
, the size of a black hole of initial mass 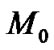 will progressively increase with sub-quantum energy accretion so that
will progressively increase with sub-quantum energy accretion so that 
 . In this way, at a time
. In this way, at a time  the black hole would blow up. For a supermassive black hole at a galactic center one would then expect that by the present time the black hole had grown up so big that its astronomical effects would be probably observable. However, one might also expect that we still are evolving on a too early time for making such observable effects observable.
the black hole would blow up. For a supermassive black hole at a galactic center one would then expect that by the present time the black hole had grown up so big that its astronomical effects would be probably observable. However, one might also expect that we still are evolving on a too early time for making such observable effects observable.
All the above results have been obtained in the case that the entanglement energy density associated with the sub-quantum potential would dominate over any other type of energy. More realistic models where contributions from dark and observable matters are taken into account as well will be considered elsewhere.
3. Violation of Classical DEC
The quantum violation of the dominant energy condition that was entailed by the benigner models described in Ref. [6] has not any classical counterpart and therefore is physically allowable. We shall investigate in what follows the sense in which that violation would permit the formation of Lorentzian wormholes and the nature of such wormholes. Choosing the simplest mixed energy-momentum tensor components and the ansatz that correspond to a static, spherically-symmetric wormhole space-time with vanishing shift function, 
 (where
(where  is the metric on the unit two-sphere), we can obtain a wormhole space-time solution from the corresponding Einstein equations containing the extra sub-quantum or entangled energy density and pressure plus the stress-energy tensor components that correspond to a Morris-Thorne wormhole [16], that is
is the metric on the unit two-sphere), we can obtain a wormhole space-time solution from the corresponding Einstein equations containing the extra sub-quantum or entangled energy density and pressure plus the stress-energy tensor components that correspond to a Morris-Thorne wormhole [16], that is

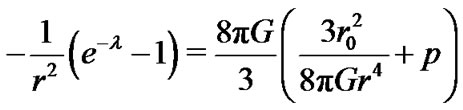

where [3-6]
 (6)
(6)
 (7)
(7)
With  and
and , supplemented by the condition
, supplemented by the condition , and a Lagrangian density from which we can derive the result that the auxiliary scalar field
, and a Lagrangian density from which we can derive the result that the auxiliary scalar field  [3-6] satisfies
[3-6] satisfies  and
and , to finally obtain
, to finally obtain
 (8)
(8)
where  plays the role of a negative cosmological constant, with
plays the role of a negative cosmological constant, with  the radius of the spherical wormhole throat and
the radius of the spherical wormhole throat and  the Planck length. Note that if
the Planck length. Note that if  was positive then no cosmic wormhole could be obtained, such as it happens for the de Sitter space.
was positive then no cosmic wormhole could be obtained, such as it happens for the de Sitter space.
To such a  -asymptotically anti-de Sitter space-time we shall continue just denoting as an asymptotically anti-de Sitter Morris-Thorne wormhole for the sake of simplicity. Metric (8) still shows an apparent event horizon at
-asymptotically anti-de Sitter space-time we shall continue just denoting as an asymptotically anti-de Sitter Morris-Thorne wormhole for the sake of simplicity. Metric (8) still shows an apparent event horizon at
 (9)
(9)
Which is the quantum-mechanical equivalent to the classical event horizon at  of the usual MorrisThorne wormhole.
of the usual MorrisThorne wormhole.
Metric (8) is by itself nevertheless an actual asymptotically anti-de Sitter wormhole because, (1) if that metric is written as
 (10)
(10)
then the new parameter [16]

 (11)
(11)
goes from 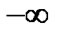 (when
(when ) to zero (at
) to zero (at ) and finally to
) and finally to  (when
(when  again), such as it is expected for a wormhole with a throat at
again), such as it is expected for a wormhole with a throat at 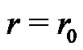 which is traversable and can be converted into a time machine.
which is traversable and can be converted into a time machine.
On the other hand (2), let us consider a three-geometry at  const. respecting spherical symmetry and
const. respecting spherical symmetry and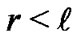 . For, it suffice choosing the slices
. For, it suffice choosing the slices , so that
, so that
 (12)
(12)
We wish now visualize the slice (12) as removed from metric (8) and embedded in three-dimensional Euclidean space which can be described by cylindrically symmetric coordinates 
 (13)
(13)
The embedding surface is describable by a function , Thus,
, Thus,
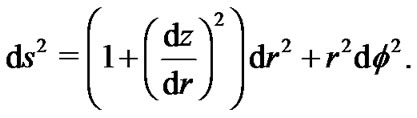 (14)
(14)
Metric (14) will be the same as metric (12) if we identify the coordinates 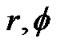 of the embedding space with those of the wormhole and we require the function
of the embedding space with those of the wormhole and we require the function  to satisfy
to satisfy
 (15)
(15)
Now, if we want the wormhole to be connectible to a asymptotically anti-de Sitter space-time, the embedding surface should flare outward at or near the throat [16]. This can be mathematically expressed by the condition , which is in fact satisfied as it can be checked from Equation (15), that is
, which is in fact satisfied as it can be checked from Equation (15), that is
 (16)
(16)
Finally (3) the considered wormhole can be shown to be traversable as a two-sphere surrounding one of its mouths where space-time is nearly anti-de Sitter can be regarded as an outer trapped surface to an observer looking through the wormhole from the other mouth.
It can be readily checked that for  there is no metric like (8) which can show properties (1) - (3).
there is no metric like (8) which can show properties (1) - (3).
However, even though the asymptotically anti-de Sitter wormhole can be converted into a time machine with line element

(17)
(where we have assumed the right mouth to move with relative velocity v with respect to the left one, so inducing time travel to be allowed,  is the acceleration of the moving mouth,
is the acceleration of the moving mouth, 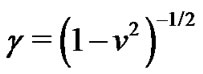 , and
, and  is form factor vanishing on the left half (
is form factor vanishing on the left half ( ) of the wormhole and increases monotonously from 0 to 1 as
) of the wormhole and increases monotonously from 0 to 1 as

Figure 1. Kruskal diagram of the  of the maximally extended space-time of the quantum-mechanical asymptotically anti-de Sitter Morris Thorne wormhole whose classical analogous is the classical asymptotically flat Morris Thorne wormhole. Null geodesics are at
of the maximally extended space-time of the quantum-mechanical asymptotically anti-de Sitter Morris Thorne wormhole whose classical analogous is the classical asymptotically flat Morris Thorne wormhole. Null geodesics are at  degrees to the vertical. The regions where V and W simultaneously have the same sign are forbidden.
degrees to the vertical. The regions where V and W simultaneously have the same sign are forbidden.
one moves rightward from the throat to the right mouth), and its metric can be maximally extended to smooth out its apparent singularity at  (Figure 1),
(Figure 1),

(18)
(with
 ,
,  where
where

and
 )these wormholes cannot insert their mouths into the asymptotically flat regions of larger universes because of obvious topological reasons. It is for this topological obstruction that the asymptotically anti-de Sitter wormholes could not enter the big trip phenomenon in a multiverse scenario [5,17-19]. Nevertheless, asymptotically anti-de Sitter wormholes can still undergo a swelling process when accreting phantom energy though their throat radius can never exceed the size of the universe where it originally existed. Let us in fact consider the process of dark energy accretion onto one such wormholes. Then, following the procedure put forward elsewhere [7-9], one can finally derive for the variation rate of the throat radius the expression
)these wormholes cannot insert their mouths into the asymptotically flat regions of larger universes because of obvious topological reasons. It is for this topological obstruction that the asymptotically anti-de Sitter wormholes could not enter the big trip phenomenon in a multiverse scenario [5,17-19]. Nevertheless, asymptotically anti-de Sitter wormholes can still undergo a swelling process when accreting phantom energy though their throat radius can never exceed the size of the universe where it originally existed. Let us in fact consider the process of dark energy accretion onto one such wormholes. Then, following the procedure put forward elsewhere [7-9], one can finally derive for the variation rate of the throat radius the expression

 (19)
(19)
where Q is positive constant, P and 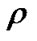 respectively are the pressure and energy density of dark energy,
respectively are the pressure and energy density of dark energy,
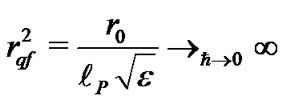 (20)
(20)
is the quantum-mechanical extension of the usual asymptotic flatness. It therefore corresponds to the value of the radial coordinate that makes flat the metric classically;  is a given function defined in terms of the components of the stress-energy tensor
is a given function defined in terms of the components of the stress-energy tensor  [13], and we have used coordinates so that
[13], and we have used coordinates so that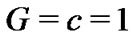 . In the present formalism there is not anything like an asymptotically flat space-time because of the existence of the entanglement energy density which in turn is the origin of the asymptotically anti-de Sitter wormholes. Evaluating then this expression at
. In the present formalism there is not anything like an asymptotically flat space-time because of the existence of the entanglement energy density which in turn is the origin of the asymptotically anti-de Sitter wormholes. Evaluating then this expression at , that is at values of the radial coordinate that approach infinity, we get the simpler rate
, that is at values of the radial coordinate that approach infinity, we get the simpler rate
 (21)
(21)
Now, for a general equation of state  and a simple quintessence field where [14]
and a simple quintessence field where [14]

(22)
with , one may integrate the above rate equation to finally have
, one may integrate the above rate equation to finally have
 (23)
(23)
with  the initial radius of the wormhole throat.
the initial radius of the wormhole throat.
For dark energy with  we see that the throat radius slowly decreases, tending to a constant radius
we see that the throat radius slowly decreases, tending to a constant radius as
as . In the case that the quintessence field behaved like phantom energy,
. In the case that the quintessence field behaved like phantom energy,  , the radius of the wormhole throat exponentially increased to reach an infinite value just at the big rip singularity time,
, the radius of the wormhole throat exponentially increased to reach an infinite value just at the big rip singularity time, . Therefore, an asymptotically anti-de Sitter Lorentzian wormhole does not give rise to the phenomenon of big trip, which requires the wormhole size to blow up before reaching the big rip singularity (Figure 2). In the most consistent situation where we use the solution
. Therefore, an asymptotically anti-de Sitter Lorentzian wormhole does not give rise to the phenomenon of big trip, which requires the wormhole size to blow up before reaching the big rip singularity (Figure 2). In the most consistent situation where we use the solution  [3-6] the increasing of the wormhole throat will take place in a rather quick fashion but yet it only tends to infinity as time does too. In this way, it also follows that neither in this case we find the big trip phenomenon Thus, all situations involving a big trip that can be eventually considered would require the presence of wormholes which are asymptotically flat, not those that are asymptotically anti-de Sitter.
[3-6] the increasing of the wormhole throat will take place in a rather quick fashion but yet it only tends to infinity as time does too. In this way, it also follows that neither in this case we find the big trip phenomenon Thus, all situations involving a big trip that can be eventually considered would require the presence of wormholes which are asymptotically flat, not those that are asymptotically anti-de Sitter.
One can finally remark that, quite the opposite to what happens with phantom energy accretion, would be expected to occur in the semiclassical thermal process that leads to the vanishing of an AdS Morris-Thorne quantum wormhole. In fact, by extending the results derived for the case of the spherically symmetric Morris-Thorne wormhole by using the so called 2 + 2 Hayward formalism [20] to the present case, we finally obtain that our quantum-mechanical AdS Morris-Thorne wormhole should be characterized by an entropy given by
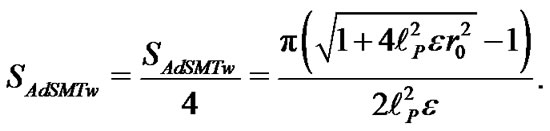 (24)
(24)
It can also be derived that these Lorentzian quantum wormholes are able to typically emit, through a semiclassical process, phantom like radiation at a negative temperature which is associated with a positive definite surface gravity  by
by
 (25)
(25)
Of course, Equations (24) and (25) reduce to their asymptotically flat Morris-Thorne values [20] in the limit where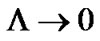 .
.
Summing up, we have derived a quantum-echanically originated asymptotically anti-de Sitter Lorentzian wormhole metric which cannot enter any big trip phenomena because of 1) the topological obstruction that the negative cosmological constant would oppose to a smooth insertion of the asymptotic wormhole regions on the universes that makes up the multiverse, and 2) a late quantum-mechanically induced swelling of the throat that postpones the emergence of the wormhole size divergence exactly to the moment at which the big rip singularity takes place. Such a wormhole shares with its asymptotically flat classical relative the essential nature of its semiclassical thermal properties, including a negative temperature and a phantom like radiation, even though its thermodynamical formulas all obviously depend on the cosmological constant  as well.
as well.
The results derived in the current paper appears to quantum-mechanically prevent the emergence of the big trip phenomena which is left to just be a classical artifact, a quantum effect that was expected to take place due to be instead induced by the bigness reached by both the wormhole throat size and the universe itself.
This work was supported by MEC under research project no. FIS2008-06332. The author also acknowledges Alberto Rozas-Fernández from IFF and Carmen L. Sigüenza of the Estación Ecológica de Biocosmologa de Medelln, Spain, for useful discussions and comments.

Figure 2. Evolution of the radius of an asymptotically anti-de Sitter wormhole throat,  , induced by accretion of phantom energy. At time
, induced by accretion of phantom energy. At time , the negative exotic mass becomes infinite and then starts steadily decreasing while the universe contracts, always keeping a smaller radius than that of the universe. There is no big trip for these wormholes but just an identification of the throat with the universe when this reaches an infinite size. Thus there could be no disruption of the causal evolution of the whole universe. Because the big rip should be dominated by still unknown quantum-gravity effects that presumably prevents the classical singularity, one is tempted to conjecture that at the big rip the universe becomes a quantum universe which is undistinguishable of the throat of a asymptotically antide Sitter wormhole.
, the negative exotic mass becomes infinite and then starts steadily decreasing while the universe contracts, always keeping a smaller radius than that of the universe. There is no big trip for these wormholes but just an identification of the throat with the universe when this reaches an infinite size. Thus there could be no disruption of the causal evolution of the whole universe. Because the big rip should be dominated by still unknown quantum-gravity effects that presumably prevents the classical singularity, one is tempted to conjecture that at the big rip the universe becomes a quantum universe which is undistinguishable of the throat of a asymptotically antide Sitter wormhole.
4. Acknowledgements
This work was supported by MEC under research project no. FIS2008-06332. The author also acknowledges Alberto Rozas-Fernandez from IFF and Carmen L. Siguenza of the Estacion Ecologica de Biocosmologia de Medellin, Spain, for useful discussions and comments.
[1] E. J. Copeland, M. Sami and S. Tsujikawa, “Dynamics of Dark Energy,” International Journal of Modern Physics D, Vol. 15, No. 11, 2006, pp. 1753-1953. doi:10.1142/S021827180600942X
[2] A. H. Guth, “Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems,” Physical Review D, Vol. 23, No. 2, 1981, p. 347-356. doi:10.1103/PhysRevD.23.347
[3] P. F. González-Díaz, “Dark Energy without Dark Energy,” AIP Conference Proceedings, Vol. 878, 2006, p. 227;
[4] P. F. González-Daz and Alberto Rozas-Fernández, Physics Letters B, Vol. 641, 2006, p. 134;
[5] P. F. González-Daz, Physical Review D, Vol. 69, 2004, Article ID 103512.
[6] P. F. González-Díaz and A. Rozas-Fernández, “Quantum Cosmic Models and Thermodynamics,” Classical and Quantum Gravity, Vol. 25, No. 17, 2008, Article ID 175023. doi:10.1088/0264-9381/25/17/175023
[7] P. F. González-Díaz, Physical Review Letters, Vol. 93, 2004, Article ID 071301;
[8] P. F. González-Díaz, Physics Letters B, Vol. 632, No. 159, 2006[9] P. F. González-Díaz, Physics Letters B, Vol. 635, No. 1, 2006.
[10] V. Faraoni and W. Israel, “Dark Energy, Wormholes, and the Big Rip,” Physical Review D, Vol. 71, No. 6, 2005, Article ID 064017. doi:10.1103/PhysRevD.71.064017
[11] A. V. Yurov, V. A. Yurov, and S. D. Vereshchagin, astro-ph/0503433.
[12] V. Faraoni, “No ‘Big Trips’ for the Universe,” Physics Letters B, Vol. 647, No. 5-6, 2007, pp. 309-312. doi:10.1016/j.physletb.2007.02.048
[13] P. F. González-Díaz and P. Martn-Moruno, Proceeding sof the 11th Marcel Grossmann Meeting on general relativity, In: H. Kleinert, R. T. Jantzen and R. Ruffini, Eds., World Scientific, New Jersey, 2008, pp. 2190-2192. arXiv:0704.1731.
[14] P. F. González-Díaz, “Wormholes and Ringholes in a Dark-Energy Universe,” Physical Review D, Vol. 68, No. 8, 2003, Article ID 084016. doi:10.1103/PhysRevD.68.084016
[15] E. Babichev, V. Dokuchaev and Yu. Eroshenko, Physical Review Letters, Vol. 93, 2004, p. 434, Article ID 021102.
[16] M. S. Morris and K. S. Thorne, “Wormholes in Spacetime and Their Use for Interstellar Travel: A Tool for Teaching General Relativity,” American Journal of Physics, Vol. 56, No. 5, 1988, p. 395. doi:10.1119/1.15620
[17] H. Everett, “Relative-State Formulation of Quantum Mechanics” Reviews of Modern Physics, Vol. 459, No. 29, 1957, pp. 454-462;
[18] A. Lin, Modern Physics Letters A, Vol. 81, 1986;
[19] S. Robles-Pérez and P. F. González-Díazm, Physical Review D, Vol. 81, 2010, Article ID 083529.
[20] P. Martn-Moruno and P. F. González-Díaz, “Thermal Radiation from Lorentzian Traversable Wormholes,” Physical Review D, Vol. 80, No. 6, 2009, Article ID 024007; P. F. González-Daz, Physical Review D, Vol. 82, 2010, Article ID 044016.