1. Introduction
There are six currently recognized conservation laws in physics. The first two (energy and momentum or simply 4-momentum) are well verified and elegantly included into General Relativity as the stress-energy-momentum tensor 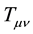 [1] . The third conservation law, angular momentum, has been experimentally confirmed from nuclear to atomic to cosmological scales.
[1] . The third conservation law, angular momentum, has been experimentally confirmed from nuclear to atomic to cosmological scales.
The fourth conservation law, charge conservation, is experimentally observed, but it shares a unique position among all six conservation laws, because it can be derived directly without any other assumptions once the E & M field tensor is determined. Thus this conservation law is automatically created by the structure of modern physics.
The fifth and sixth conservation laws (baryon number and lepton number) are purely based on experimental observations of elementary particle interactions and lead to conclusions such as: “The proton does not decay since it is the lowest mass baryon.” Sensitive tests for proton decay have agreed with this conclusion [2] .
2. Charge Conservation Is Unique
We mentioned above that charge conservation is not just an experimental conservation equation like energy or momentum or baryon number, but can be itself derived from the basic physical theory. We summarize that derivation here for clarity because it leads directly to many more conservation laws.
The key principle is that the current density is derived as the divergence of an antisymmetric tensor. That tensor is called the electromagnetic field tensor 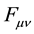 shown in Equation (1), where E and B are the familiar electric and magnetic fields.
shown in Equation (1), where E and B are the familiar electric and magnetic fields.
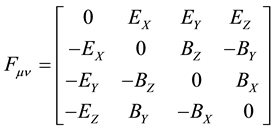 (1)
(1)
The charge density 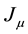 is then defined as the divergence of
is then defined as the divergence of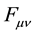 , as shown in Equation (2).
, as shown in Equation (2).
 (2)
(2)
To show that 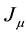 is a conserved quantity, we again take its divergence in Equation (3) and recognize that since the E & M field tensor
is a conserved quantity, we again take its divergence in Equation (3) and recognize that since the E & M field tensor 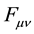 is antisymmetric, we can switch the indices of
is antisymmetric, we can switch the indices of 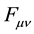 by adding a minus sign in Equation (3). Then we use the commutation of partial derivatives to switch the
by adding a minus sign in Equation (3). Then we use the commutation of partial derivatives to switch the 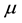 and
and 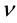 raised derivatives, and we return to minus the divergence of the current density.
raised derivatives, and we return to minus the divergence of the current density.
If the divergence of the current density equals its own negative, then it equals zero as summarized in Equation (4). This is the definition of a conserved quantity, when we can define a 4-vector such as 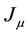 whose divergence vanishes. The conserved quantity is the time component
whose divergence vanishes. The conserved quantity is the time component 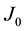 (usually denoted by
(usually denoted by 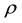 and called charge density) summarized in Equation (5), and the vector component shows the flow of charge density.
and called charge density) summarized in Equation (5), and the vector component shows the flow of charge density.
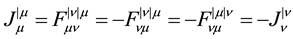 (3)
(3)
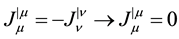 (4)
(4)
![]() (5)
(5)
Equation (6) shows a more familiar form of the current conservation law. It says that the time derivative of the charge density matches the divergence of the current density. Here we switch to the more familiar raised index so that the derivatives are simply the normal derivatives. Here 0 is the time component of J (charge density![]() ) and
) and![]() , the three spatial coordinates for the current density
, the three spatial coordinates for the current density
![]() (6)
(6)
3. Now Generalize
Since charge conservation can be derived from the basic theory of electromagnetism, we call charge conservation an “automatic conservation law”. It comes about simply because current density is the divergence of an antisymmetric tensor. Despite being automatic, it has been extremely useful in physics.
But now we can get another conservation law for an entirely different type of charge by creating any other antisymmetric second rank tensor. Suppose we contract the E & M field tensor with itself to get a scalar term![]() , invariant in all coordinate systems as shown in Equation (7).
, invariant in all coordinate systems as shown in Equation (7).
![]() (7)
(7)
Now multiply the usual E & M field tensor by the scalar field![]() , and we have a new antisymmetric E & M tensor. It too will generate its own conserved charge we call
, and we have a new antisymmetric E & M tensor. It too will generate its own conserved charge we call![]() , quite different from the usual charge J0 as shown in Equation (8).
, quite different from the usual charge J0 as shown in Equation (8).
![]() (8)
(8)
![]() is not just a scaled version of the standard current density
is not just a scaled version of the standard current density![]() , but weights the current density by the scalar E & M density
, but weights the current density by the scalar E & M density ![]() and then adds the dot product of the electric field
and then adds the dot product of the electric field ![]() times the gradient of the scalar E & M density
times the gradient of the scalar E & M density![]() . This new charge density is thus a completely different conserved charge density. Furthermore, since this charge comes from an antisymmetric tensor, the same derivation that supports normal charge as a conservation law will support this new charge as an additional conservation law.
. This new charge density is thus a completely different conserved charge density. Furthermore, since this charge comes from an antisymmetric tensor, the same derivation that supports normal charge as a conservation law will support this new charge as an additional conservation law.
We conclude that every elementary particle must have a second independent electro-magnetic charge associated with it that must be conserved under all interactions.
4. Generalize to Any Power
This same derivation could be used for any power of the E & M scalar density![]() , and each one will produce a rigorously conserved charge different from the others. Thus there will be a string of charges, we call hypercharges, different from the conventional charge which characterize each elementary particle and which all must be conserved under every type of interaction.
, and each one will produce a rigorously conserved charge different from the others. Thus there will be a string of charges, we call hypercharges, different from the conventional charge which characterize each elementary particle and which all must be conserved under every type of interaction.
5. A Gravity-E & M Conservation Law
Suppose we replace the scalar E & M field ![]() with the fully contracted Riemann curvature tensor R [1] , which is a well known scalar involving the gravitational field. Now we will get a conservation law for gravity-E&M interactions that applies to every possible gravitational solution with E & M fields present. Any solution for an electrically charged black hole would have to satisfy this hypercharge conservation equation.
with the fully contracted Riemann curvature tensor R [1] , which is a well known scalar involving the gravitational field. Now we will get a conservation law for gravity-E&M interactions that applies to every possible gravitational solution with E & M fields present. Any solution for an electrically charged black hole would have to satisfy this hypercharge conservation equation.
![]() (9)
(9)
6. Strong-Weak-E & M Conservation Law
Suppose we consider the stress-energy-momentum tensor ![]() [1] , which is used as the source for gravitation. It includes strong, weak and E & M contributions. Its contracted form is called
[1] , which is used as the source for gravitation. It includes strong, weak and E & M contributions. Its contracted form is called![]() , which we can use instead of
, which we can use instead of ![]() to multiply the antisymmetric tensor
to multiply the antisymmetric tensor![]() . Now we have a new antisymmetric tensor which will give us a new conserved charge that represents the interaction between all those fields as shown in Equation (10). Any problem involving mass and electric fields will have to satisfy this hypercharge conservation equation.
. Now we have a new antisymmetric tensor which will give us a new conserved charge that represents the interaction between all those fields as shown in Equation (10). Any problem involving mass and electric fields will have to satisfy this hypercharge conservation equation.
![]() (10)
(10)
Once again, by varying the power applied to![]() , we get an infinite number of stress-energy-momentum-E & M charge densities―all of which must be exactly conserved according to our current set of physical laws.
, we get an infinite number of stress-energy-momentum-E & M charge densities―all of which must be exactly conserved according to our current set of physical laws.
7. Not So Demanding as It Seems
We have shown that there is an infinite set of independent conservation laws coupling every known field into every other known field. Overall it seems so restrictive that we might wonder how the universe moves at all. However, the benefit of conservation laws like this is that they are automatic. As the fields change, the symmetries enforce these conservation laws. Thus one might question how useful they are.
8. Why Haven’t We Seen These Other Conservation Laws?
The usual charge density produces a ![]() field that can be measured macroscopically, just as can mass and energy. The higher order charges we derived above are much shorter range since they are multiplied by the function
field that can be measured macroscopically, just as can mass and energy. The higher order charges we derived above are much shorter range since they are multiplied by the function ![]() or
or![]() . The resulting hypercharge density drops off as
. The resulting hypercharge density drops off as ![]() or faster depending on the particle or field. Because of their very short range, these new conservation laws do not create any effect macroscopically. Thus they would be expected to show up only indirectly when we see conservation laws appearing for no other obvious reason.
or faster depending on the particle or field. Because of their very short range, these new conservation laws do not create any effect macroscopically. Thus they would be expected to show up only indirectly when we see conservation laws appearing for no other obvious reason.
9. Elementary Particles
All these charge densities have the common property that for elementary particles they drop to zero rapidly when the E & M field, strong and weak fields drop to zero. Thus we find that charge is a very useful concept for an elementary particle because it is a well isolated system of non-zero fields. Since charge is globally conserved, the isolation of each elementary particle ensures that each particle has well defined charges and that every interaction between elementary particles conserves total charge.
Now, however, we see that each elementary particle does not have just one charge but many more additional hypercharges associated with it. Since the internal field structure of a proton is very different from an electron, we would assume that the higher order charges would also be quite different. This factor alone could prevent a proton from decaying into a muon or a positron unless some third particle could carry away the exact difference in hypercharge between them.
We conclude baryon and lepton conservation have the qualities that we would expect from hypercharge conservation. The do not come from any primary principle except that they are experimentally observed not to decay out of their families. If each type of particle (lepton, baryon for two) has its own unique spectrum of hypercharge, then one type cannot decay into another type unless there is a third particle (or set of particles) that can carry away the exact difference in hypercharges. The observation that higher mass baryons do decay indicates that the family of baryons share a unique and common internal hypercharge structure. The same will be true for the family of leptons.
10. Summary
We have shown rigorously that our current models of physics predict a vast set of different conserved charges, called hypercharges, which couple together every known field. We have concentrated more on the E & M hypercharges here, because they are more familiar, but there will also be strong and weak hypercharges. We conclude that elementary particles are isolated islands of fields―strong, weak and electromagnetic―each with their own charge and hypercharges, which must all be conserved under every type of interaction.
Since there appear to be so many degrees of freedom that must be conserved in any decay of elementary particles, this level of constraint suggests that there may be forms of radiation that can carry away excess hypercharge to enable some of the decays and interactions to proceed. The other option is that only a few profiles of conserved charges are stable and become what we call particles. Since each family has such a different hypercharge structure from the other families, one type cannot change into the other without some process that adjusts the internal charge profiles.
We suggest that baryon conservation and lepton conservation are simply two more automatic charge conservation laws involving fields with shorter ranges than electromagnetism.