Effect of Base Width and Stiffness of the Structure on Period of Vibration of RC Framed Buildings in Seismic Analysis ()
1. Introduction
Estimation of seismic base shear requires the fundamental natural period of vibration T of the building. However for the building configuration adopted and the construction material chosen, it is not always possible to exactly determine from theoretical considerations, that is, through detailed dynamic analysis. Hence, empirical formulae obtained through experimentally observed behavior of buildings are utilized [1] - [3] . The stiffness contribution of many non structural elements, such as in-fill masonry panels [4] [5] , also considered to derive period formula in different countries. For this reason, the empirical expression for T may be specific to each country. The approximate fundamental natural period of vibration (Ta) in second of a moment resisting frames building without brick infill panels may be estimated by empirical expression given in Indian seismic code IS1893 (Part-1)-2002 [6] .
 for RC frame building (1.1)
for RC frame building (1.1)
 for steel frame building (1.2)
for steel frame building (1.2)
 for all other buildings. (1.3)
for all other buildings. (1.3)
In past, most countries used to allow estimation of T by any “properly” substantiated method of analysis. This may, in some situations, lead designers to arrive at unusually large estimation of T, as a result, lower seismic design forces from dynamic analysis of bare skeletal frame ignoring nonstructural elements, such as partitions and un-reinforced brick filler walls. A higher estimate of T will lead to lower design forces.
Recent Indian seismic design code IS1893 (Part-1)-2002 allows the estimation of T by any of the following methods:
・ Experimental observations on similar buildings (which almost never happens in practice).
・ Any rational method of analysis (referring to dynamic analysis), or
・ Using the empirical expressions prescribed in the code IS1893 (Part-1)-2002.
The fundamental period can be evaluated using simplified expressions (1.1) to (1.3) found in codes, which are based on earthquake recordings in existing buildings, laboratory tests, numerical or analytical computations. These technical codes provide expressions which depend on basic parameters such as building height or number of storeys. Building periods predicted by these expressions are widely used in practice although it has been pointed out by Amanat and Hoque (2006) [7] and Verderame, Iervolino and Manfredi (2010) [8] that there is scope for further improvement in these equations since the height alone is inadequate to explain period variability. It is also known that the period of a reinforced concrete (RC) frame structure differs depending on whether the longitudinal or transverse direction of the structure is considered.
The aim of this study is to find the effect of base width and stiffness of the structure in order to predict the fundamental period of vibration of reinforced concrete buildings with moment resisting frames. A few examples of dynamic analysis are presented in this study in order to show that the base width should also be incorporated in the formula to evaluate period of vibration; another point of great interest is to understand the effect of stiffness of the structure in the evaluation of period of vibration.
2. Literature Study
The value of the fundamental period needs to be as accurate as possible in earthquake resistant designs, as lower the value of time period, higher will be the base shear and vice versa, with a special emphasis on designs which are based on either linear static (or lateral force) methods or performance level. Buildings are usually designed for seismic resistance using elastic analysis, but most will experience significant inelastic deformations under large earthquakes.
Thus, building codes extract seismic loads of inelastic designs from a linear spectrum, which is dependent on the fundamental period of structure, and ground zone type. In other words, in current seismic code provisions, seismic forces estimation using design spectra requires either implicitly the use of empirical equations for the fundamental period determination or more specifically detailed dynamic analysis.
Since the predicted fundamental period is used to obtain the expected seismic load affecting the structure, a precise estimation of it is important for the safety of the applied procedure in the design steps and consequently in the future performance of the structure after it is constructed. The fundamental period of vibration required for the simplified design of RC structures has been calculated for many years using a simplified formula relating the period to the height of the building. One of the first formulae of this type was presented over 30 years ago in ATC3-06 (ATC, 1978) [9] given as
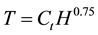 (2.1)
(2.1)
where:
H―height of the structure [m] and;
Ct―constant depending on the structure type.
The coefficient Ct is calibrated in order to achieve the best fit to experimental data.
Crowley and Pinho [10] used a computer solution SeismoStruct (Seismosoft Ltd|Via Panoramica 1910, 98100 Messina, Italy) to model RC frames corresponding to actual buildings (three to eight stories) from five different European countries exposed to earthquake action (Greece, Italy, Portugal, Romania, and ex-Yugoslavia). The two dimensional RC frames were modeled as bare frames, fully infilled frames and infilled frames with openings, and a weighted average of the period of vibration of these types of frames was then calculated by taking into account their frequency of occurrence within the building stock. The equations for calculating the period of uncracked infilled buildings using a weighted mean period of vibration for each frame was represented as
 (2.2)
(2.2)
To derive period formula for fully infilled frames and the infilled frames with openings, the same models with reduced member stiffness were used. The study results in a simplified period-height equation for use in the assessment of existing RC buildings, taking due account of the presence of infill panels.
 (2.3)
(2.3)
M. Hadzima et al. [11] seven different equations proposed in their study in order to determine more accurate expressions for the elastic period they considered seven basic expressions which, in addition to the number of floors, take into consideration each of the following:
・ The number of bays parallel to the considered direction;
・ The ratio between the number of bays in the longitudinal and transversal directions;
・ The product between the number of bays in the longitudinal and transversal directions.
Following are the expressions proposed to evaluate period of vibration:
 (2.4)
(2.4)
 (2.5)
(2.5)
 (2.6)
(2.6)
 (2.7)
(2.7)
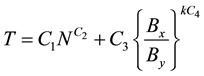 (2.8)
(2.8)
 (2.9)
(2.9)
 (2.10)
(2.10)
where N is the number of storeys, B is the number of bays of the building parallel to the considered direction, Bx is the number of bays in longitudinal direction, By is the number of bays in transversal direction, k is a constant which has a value of 1 when the period in the longitudinal direction is to be determined and a value of 1 when the period in the transversal direction is to be determined and C1, C2, C3 and C4 are (unknown) parameters that need to be determined. The parameters of the expressions are determined by performing nonlinear regression analysis.
Goel and Chopra (1997) collected data measured from eight Californian earthquakes, from 1971 (San Fernando earthquake) until 1994 (Northridge earthquake) and different formulas were proposed resulting from semi empirical analysis, with the best-fit plus 1 standard deviation recommended for displacement-based assessment, whilst the best-fit minus 1 standard deviation recommended for conservative force-based design [12] :
 (2.11)
(2.11)
 (2.12)
(2.12)
where H is the height of the structure [m].
Gerardo M. 2010 [8] evaluated elastic period for both main directions of the buildings of the considered sample, and regression analysis is employed to capture the dependency of the elastic dynamic properties of the structures as a function of mass and stiffness, based on the results of the analyses a power-law regression was carried out as a function of height. In the comparison with Eurocode 8 formulas existing buildings show systematically larger periods for those herein analyzed. In particular, gravity loads designed buildings, featuring a 3D structural system, seem to require a twofold definition of period referring to the two directions. Therefore, height alone seems inadequate to explain period variability and the results of this study suggest that. Also a global parameter (e.g., plan area) should be added in simplified relationships for rapid period evaluation. Therefore, an expression which includes also the plan area is considered in the following equations.
 (2.13)
(2.13)
where S is the product of the two principal plan dimensions of the building Lx and Ly.
3. Methodology
Here in this paper a 25 story RC frame buildings square shaped in plan is analyzed using computerized solution STAAD V8i [13] with the following building configuration.
1) Type of structure―Multistory rigid jointed plane frames.
2) No of storey―G + 24, Twenty five stories.
3) Seismic zones―III.
4) Floor height―3.6 m.
4b) Depth of foundation―2.0 m.
5) Building height―92.0 m (90.0 + 2.0).
6) Building details―As per Table 1 & Figure 1 & Figure 2.
7) Size of beams―0.30 m × 0.60 m.
8) Walls―a) External―200 mm.
b) Internal―100 mm.
9) Thickness of slab―150 mm.
10) Imposed load [14] ―4.00 kN/m2.
11) Floor finish―1.00 kN/m2.
12) Water proofing―2.500 kN/m2.
13) Specific wt. of RCC―5.00 kN/m3.
14) Specific wt. of infill―20.00 kN/m3.
15) Materials used―Concrete M-25 and reinforcement Fe-415.
16) Earthquake load―As per IS1893 (Part-1)-2002.
17) Type of soil―Type-II, medium soil as per IS-1893.
18) ![]()
(Ec is short term static modulus of elasticity in N/mm2).
19) ![]()
(Fck is characteristic cube strength of concrete in N/mm2).
20) Static analysis―Equivalent static lateral force method.
21) Dynamic analysis―Using response spectrum method.
22) Software used―STAAD-Pro for both static and dynamic analysis.
23) Fundamental natural period of building―As per IS1893 (Part-1)-2002.
24) Zone factor Z―As per IS1893 (Part-1)-2002 for different zones as per clause 6.4.2.
As mentioned in Table 1, total 36 numbers of square shaped building in plan and 92.00 m in height i.e. 25 (G + 24) storied buildings with the different base dimensions (L × B in Figure 1) ranging from 24 m × 24 m to 72 m × 72 m having 6 panels of bay width (a in Figure 1) 4 m to 12 m each are analyzed in this study to examine the effect of base dimensions in the period of vibration of the building, for mentioned building geometries of the building each building configuration is again analyzed by changing the size of the columns from 1.0 m × 1.0 m, 0.75 m × 0.75 m 0.6 m × 0.6 m and 0.5 m × 0.5 m.
Here in this study 20 modes of vibration are considered to get 90% participation. Fundamental period of vibration can be determined by using code based formulae which are empirical formulas based on building height and fundamental mode of vibration of building may be determined by one of the methods of dynamic analysis mentioned in IS code.
4. Results
In this paper 36 buildings with different base dimensions are analyzed, keeping the height of the building same i.e. 92 m, it is observed in the analysis that, cut off modes required to be 20 to get the 90% participation. Here it can easily be observed that the time period of the building based on the code based formula comes out to be 2.1915 sec without considering infill walls, as the same are not modeled in the analysis. Period of the building so calculated by the code formula will remain same in all the 36 cases which are compared with the value of time period derived from the dynamic analysis, the value of time period for the first mode of vibration are compered in the succeeding tables.
5. Conclusions
Results of the analysis are depicted in Tables 2-6, in which values of the fundamental period of vibration derived from the analysis are tabulated along with the base dimensions. Separate tabulations are made for column dimensions 1.00 × 1.00 m to 0.50 × 0.50 m. Considering the base case as building with base dimension of 24 m, values of the time period of different buildings are compared and percentage variations are depicted in these tables. Similarly percentage variations of base dimension are also tabulated.
From the Table 2, it can be observed that the value of Tmax i.e. fundamental period of vibration corresponding to first mode of vibration varies from 3.738 sec to 12.6483 sec for a building with base width of 24 m and 72 m respectively having column size as 1.0 m × 1.0 m. Similarly from the Table 5, it can be observed that the
![]()
Table 2. Comparison of time period with base dimension (column size 1.0 m × 1.0 m).
![]()
Table 3. Comparison of time period with base dimension (column size 0.75 m × 0.75 m).
![]()
Table 4. Comparison of time period with base dimension (column size 0.60 m × 0.60 m).
![]()
Table 5. Comparison of time period with base dimension (column size 0.50 m × 0.50 m).
![]()
Table 6. Comparison of time period with stiffness variation (base case col size 1.00 × 1.00 m).
value of Tmax i.e. fundamental period of vibration varies from 4.723 sec to 15.023 sec for a building with base width of 24 m and 72 m respectively having column size as 0.50 m × 0.50 m, against the time period of 2.1915 sec derived on the basis of code based formula. It is observed that values of time period which comes out of dynamic analysis are higher than those derived from code base formula and also values of period of vibration increase with increase in base dimension, which ultimately reduces the base shear. Considering the base case as a building with base width of 24 m, variation in time period comes out to be 22.21% to 238.66% whereas in base dimension is observed to be 25% to 200%. Hence it can be concluded that percentage variation in time period is almost identical to the percentage variation of base dimension. Similar results are tabulated in Tables 3-5.
Table 6 depicts the changes observed in value of period of vibration by changing column dimensions from 1.0 m × 1.0 m to 0.50 m × 0.50 m. It is observed that time period increases by almost 26.47% for 24 m wide building to 18.78% for 72 m wide building.
In view of the results obtained in the analysis, values of the time period of vibration differ substantially, and the difference comes out to be on higher side, which results in reduction in base shear and makes the structure economical. Further conclusions can be drawn for the changes made in column dimensions i.e. reduction in column sizes increase in the value of time period. Hence period formulae mentioned in seismic codes need to be reviewed with respect to base width and stiffness of the structure.
NOTES
*Authors have presented this paper in SEC2014 at IIT Delhi.