Gravitation and Electromagnetism Conciliated Following Einstein’s Program ()
1. Introduction
The conciliation of gravitation with electromagnetism is one of the most present resisting problems in physics. The main difficulty lies in the fact that, until now, gravitation is still described by general relativity, in a classical and determinist framework, while electromagnetism, incorporated in the standard model, is described by a quantum field, in a probabilistic framework.
For the physicists, the whole universe is nowadays theoretically described by the standard model, which forms a consistent system. It is constituted by matter interacting through three different kinds of forces. All are composed of fundamental particles which derive from relativist quantum fields, and behave either as waves or as particles. The standard model has been validated in 2012 by the B.E.H, or Higgs, boson detection, representing its crowning. Since it does not include gravitation, it describes only a partial aspect of the universe. It is admitted as posterior to Planck’s era.
By comparison, gravitation is well described by general relativity, based on a continuous field [1] -[5] . It has been largely confirmed by numerous experiments and by its theoretical consequences and practical applications. The graviton, as the quantum particle mediating for gravitation interaction, has not yet been detected and validated [6] [7] . Consequently, until having proof to the contrary, gravitation remains well described by general relativity, in a classical framework.
In extension of general relativity and of his different discoveries, including in quantum physics, such as the stimulated emission, Einstein had proposed a consistent approach for physics, symmetrical to the standard model [1] . He privileged a continuous field, leaning on physical representations of phenomena, before their more precise mathematical description.
It has been supported, and validated, by the International Legal Metrology Organization. In one hand, the speed of light in vacuum is admitted as a “pure”, or primary, fundamental constant in experimental physics, with its numerical value strictly fixed. In other hand, the standard for measures of time is based on the period an electromagnetic oscillation.
In a previous article [8] , we showed how the Einstein’s program forms a consistent system for universe description, beside the standard model. It allows us to complete the universe grasp, like both eyes give us access to tridimensional vision, or both ears to stereophonic audition. It founds upon a scalar field propagating at light velocity. Matter corresponds to standing waves, and electromagnetism, as a quantum interaction, to their adiabatic variations. Classical domain restricts to the geometrical optics approximation, when frequencies are infinitely high, and then hidden [9] - [12] .
In this article we propose to show how the Einstein’s program permits to conciliate gravitation and electromagnetism. Since both act as interactions of matter, they derive from variations of its energy E = mc2. Electromagnetic interaction energy corresponds to the mass variation dE = c2dm, while gravitation energy is linked to variation of the light velocity dE = mdc2. Contrarily to gravitation, only electromagnetic interaction energy dE = hdν = mdc2, derives directly from the wave character of matter with E = hν = mc2, as an adiabatic variation.
2. History
The historical development of interaction properties of matter with gravitation, and of interaction properties of charges with electromagnetism, showed from the beginning, how they were all closely linked together.
Gravitation was the first interaction, discovered and formalized in the 17th century. The Newton’s attractive force
F = Gmm'/r2 (1)
exerted between two localized masses m, m', separated by a distance r, introduced in physics the concept of force, applied respectively to point-like gravity centers, together with the concept of particle. Afterward, one century later, the problem of harmonizing electromagnetism began to arise, when the Coulomb’s force
F = kqq'/r2 (2)
between electric charges q, q', revealed similar to (1), beyond the fact that it is attractive or repulsive, depending the signs of the charges. Both equations form parts of the same Newtonian field, acting instantaneously between two point particles in vacuum. In addition, the charges have necessarily matter as support.
Special Relativity replaced the instantaneous action at a distance between particles, by an action propagating at speed of light c, emphasizing that it occurred in vacuum. Henceforth, the speed of light plaid a fundamental role in physics, particularly in the space-time framework, as a link between space and time coordinates.
However, in spite of its extension feature, in Einstein’s equation of General Relativity,
Rij − gijR/2 = χTij (3)
the local variations of space-time properties, characterized by the metric tensor gij, leading to a curvature R, prevented to maintain it still empty. (Despite its usefulness, we did not consider the cosmologic constant Λ, since the additional term gijΛ may figure either in any side, according to its physical consequences). The left side of (3), which is the principal feature of the theory, describes the gravitation properties of space-time, through a classical continuous field propagating at light velocity c, as resulting from the tensors gij and its derivative Rij. They arise themselves from the matter-energy tensor Tij of the right side, acting as sources, globally in motion with a speed v strictly inferior to c, and gathering different phenomenological and theoretical properties of matter-energy, through masses and interactions.
Einstein’s equation law for gravitation (3) derives directly as an extension of Newton’s law (1). (It is known that (1) arises as an approximation of (3), remaining largely sufficient for usual terrestrial, and even spatial, applications for moving matter. It becomes insufficient for GPS because it concerns electromagnetic rays propagation). Nevertheless, passing over from (1) to (3) was conditioned by the transformation of Coulomb’s equation (2) on behalf of static Poisson’s equation ∆V = −4πρ for electricity, after introducing a space-distributed potential V in place of force F, and continuous charge density ρ, in place of point-like charge q. It led to the Maxwell’s equations. According to Einstein, “The formulation of these equations is the most important event in physics since Newton’s time, not only because of their wealth of content, but also because they form a pattern for a new type of law… The characteristic features of Maxwell’s equations, appearing in all other equations of modern physics, are summarized in one sentence. Maxwell’s equations are laws representing the structure of the field.” [2] . Nowadays, it still appears that, “One could believe that it would be possible to find a new and secure foundation for all physics upon the path which had been so successfully begun by Faraday and Maxwell. Accordingly, the revolution begun by the introduction of the field was by no means finished” [1] .
At the present time, in view of physics unification into the standard model of particles, gravitation remains, after almost one century of efforts, the last one to be quantified, in order to rejoin the three others. Einstein’s Equation (3) gathers together separately in either side, without fusing them, not only gravitation and electromagnetism but also opposite entities, like fields propagating at light velocity c, and localized matter-energy.
This is why, despite of his awareness of general relativity achievement, Einstein was “dissatisfied with the dualism of a theory admitting two kinds of fundamental physical reality: on the one hand the field and on the other hand the material particles. It is only natural that attempts were made to represent the material particles as structures in the field, that is, as places where the fields were exceptionally concentrated. Any such representation of particles on the basis of the field theory would have been a great achievement... This theory having brought together the metric and gravitation would have been completely satisfactory of the world had only gravitational fields and no electro-magnetic fields. Not it is true that the latter can be included within the general theory of relativity by taking over and appropriately modifying Maxwell’s equations of the electro-magnetic field, but they do not then appear like the gravitational fields as structural properties of the space-time continuum, but as logically independent constructions. The two types of field are causally linked in this theory, but still not fused to an identity.” [1] .
3. The Einstein’s Program
In extension of general relativity and of his different discoveries, including in quantum physics, such as the stimulated emission, Einstein had proposed a consistent approach for physics, which appears at the present time, as symmetrical to the standard model: “We have two realities: matter and field… We cannot build physics on the basis of the matter concept alone. But the division into matter and field is, after the recognition of the equivalence of mass and energy, something artificial and not clearly defined. Could we not reject the concept of matter and build a pure field physics?… We could regard matter as the regions in space where the field is extremely strong. In this way a new philosophical background could be created… Only field-energy would be left, and the particle would be merely an area of special density of field-energy. In that case one could hope to deduce the concept of the mass-point together with the equations of the motion of the particles from the field equations― the disturbing dualism would have been removed… One would be compelled to demand that the particles themselves would everywhere be describable as singularity free solutions of the completed field-equations. Only then would the general theory of general relativity be a complete theory.” [1] .
As a general manner, new technologies evolve in accordance with the Einstein’s program, when they are substituting, progressively and almost systematically, mechanical devices by electronic devices, based upon electromagnetic field in place of matter. For instance, instead of printing documents on paper, they are rather numerically recorded. What is more specific is that, decades after the Einstein’s program was set, physicists had begun to bring it into effect, when they replaced international standards of length and time, based on matter since two centuries, by electromagnetic standards, based on the period of a continuous field propagating at the speed of light. As far back as 1905, when Einstein established special relativity theory, he used a light ray, and not a material rod, to measure the distance of a moving body. He anticipated the international standard of length adopted in 1960 by the International Legal Metrology Organization. Now it derives from the second, defined by the radiation period of the cesium 133 atom, and by, the speed of light in vacuum, admitted as fundamental, with its numerical value strictly fixed. This allows to measure durations with 10−18 precision. Such measures, carried out by electromagnetic frequencies reduction ratio, are the more precise in physics at the present time [13] [14] .
Thus, not only the Einstein’s program gave numerous proofs of its validity, but it presents itself as precise means to investigate the problem of gravitation and electromagnetism conciliation. The more especially as gravitation has strongly resisted to its quantification, since almost one century. For this purpose we point out two of their main characteristic features.
The first one is explicit in the program, and was emphasized by Einstein since 1905 in special relativity: the speed of light c. Its basic role in whole experimental and theoretical physics has been legally confirmed in international standards, as a “pure” or primary fundamental constant, with its value numerically fixed. It is the speed of propagation in vacuum for gravitation and electromagnetism interactions. On another hand, the legal standard of time leans on a frequency of oscillation of a field propagating at the speed of light.
4. Electromagnetism and Special Relativity
4.1. Standing Field Kinematics
In previous works [15] [16] , we showed how kinematic properties for standing waves of a scalar field propagating at light velocity c, with constant frequency w and velocity v, are formally identical with mechanic properties of isolated matter. The Lorentz transformation, which plays a fundamental role in special relativity, is specific of standing waves.
Starting from a scalar field e propagating at light velocity c, we are assured that all following consequences are relativistic. The general harmonic solutions of the d’Alembertian’s equation
e = De − (1/c2)(¶2e/¶t2) = 0, ¶m¶me = 0 (4)
may be reduced to two kinds of elementary ones, according to their kinematic, or their geometric, properties. In the first case, we find progressive waves propagating at speed of light in opposite direction, like cos(w0t0 ± k0x0), and standing waves with separated variables x0, t0, and distinct functions of space u0(k0x0), and of time y0(w0t0), e0(x0, t0) = u0(k0x0)y0(w0t0) = cos(w0t0)cos(k0x0), with frequency w0 = k0c. Since they oscillate locally, they define then a rest system for coordinates (x0, t0). Since the functions u(k0x0) and y0(w0t0) are independent, the frequency w0 is necessarily constant in (1/u0)D0u0 = (1/y0)(¶2y0/c2¶t02) = −k02 = −w02/c2 = constant. Progressive and standing waves can be considered either as basic, or as composed from others since
cos(w0t0 + k0x0) + cos(w0t0 − k0x0) = 2cos(w0t0)cos(k0x0), (5)
cos(w0t0)cos(k0x0) + sin(w0t0)sin(k0x0) = cos(w0t0 − k0x0) (6)
when the frequencies of opposite progressive waves are different in a system of reference (x, t),
cos(w1t − k1x) + cos(w2t + k2x) = 2cos(wt − bkx)cos(kx − bwt), (7)
by identification with (5), they form a standing wave with main frequency 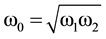 at rest. It becomes w = (w1 + w2)/2 = kc, when in motion with a speed v = bc = (w1 − w2/w1 + w2)c, leading to the Lorentz transformation between the systems of reference(x0, t0) and (x, t), and to its whole consequences.
at rest. It becomes w = (w1 + w2)/2 = kc, when in motion with a speed v = bc = (w1 − w2/w1 + w2)c, leading to the Lorentz transformation between the systems of reference(x0, t0) and (x, t), and to its whole consequences.
The geometric properties of standing waves are described by the function of space u(k0x0), obeying Helmholtz’s equation D0u0 + k02u0 = 0. Its solutions verify Bessel spherical functions, and particularly its simplest elementary solution, with spherical symmetry, finite at origin of the reference system, and representing a lumped function,
u0(k0r0) = (sink0r0)/(k0r0), (8)
In geometrical optics approximation, when the frequency is very high and tends towards infinity w0 = k0 ® µ, the space function u0 tends towards Dirac’s distribution u0(k0r0) ® d(r0). The standing wave of the field behaves as a free classical material particle isolated in space.
From a kinematical point of view, the central extremum of an extended standing wave, either at rest or in motion, is appropriate to localize its position x0, exactly like the centre of mass for a material system. It verifies
Ñ0u0(x0) = 0. (9)
The four-dimensional Minkowski’s formalism traduces invariance properties of standing waves at rest, when they move uniformly. Confirmation is found into invariant quantities obtained from four-quantities, such as coordinates xmxm = x02 or xmxm = c2t02, and functions umum = u2(x0) or ymym = y2(t0). Their space-like or time-like characters are absolute, depending of their refering quantities defined in the rest system, in which the separation with respect to space or time occurs.
In order to point out their constant frequency, we express them as
e(wt, kx) = u(kx, bwt)expi(wt − bkx) φ = wt − bkx (10)
In special and general relativity, the equations are based on particles, as singularities, moving on trajectories. They lean then directly upon geometrical optics approximation. The periodic equations, generic of standing fields, are hidden. The space coordinates xα, involved in the metric, are point-like dynamical variables, and not field variables r which would describe an extended repartition in space.
4.2. Standing Field Dynamics
All above equations are unlimited with respect to space and time, since x or t may become infinite. Usually, one imposes boundary conditions, in which matter acts either as a source fixing the frequency w, or as a detector annealing it, as well as a geometrical space boundary fixing the wavelength λ through k = 2π/λ. This is not felicitous from relativistic consistency, since space and time operate separately. In addition, matter is heterogeneous with regard to field. In order to remain in homogeneous frame, we rather consider boundaries provided by wave packets. Two progressive waves with different frequencies w1, w2 propagating in the same direction at light velocity, give rise to a wave packet propagating in the same direction at light velocity, with a main wave with frequency w = (w1 + w2)/2, modulated by a wave with frequency bw = (w1 − w2)/2 = Dw/2 = Dkc/2 and wavelength Λ = 2p/bk and period T = Λ/c. Since b < 1, the modulation wave acts as an envelope with space and time extensions Dx = Λ/2, Dt = T/2, leading to well known Fourier relations DxDk = 2p and DtDw = 2p.
Then, Fourier relations represent homogeneous boundary conditions for the scalar field e. From a physical point of view, they must be compulsory associated with the d’Alembertian’s Equation (4) in order to complete them, and to emphasize that the field cannot extend to infinity with respect to space and time.
When the frequencies difference bw = (w1 − w2)/2 = Dw/2 << w is very small, it can be considered as a perturbation with respect to the main frequency, bw = δw. Then a wave packet can be assimilated to a progressive monochromatic wave with frequency Ω = w ± δw, inside the limits fixed by the component frequencies w1 = w + δw and w2 = w − δw. By difference with standing waves frequencies, which must be constant and monochromatic, progressive fields solutions of (4), may be more complex, with frequencies varying with space and time. An almost monochromatic wave is characterized by a frequency Ω(x, t), varying very slowly around a constant w
Ω(x, t) = K(x, t)c = w ± δΩ(x, t) δΩ(x, t) << w w = constant. (11)
From a physical point of view, we recognize the definition of an adiabatic variation for the frequency [17] . We can then expect that all following properties of almost fields occur inside such a process. Instead of admitting constant frequencies w of elementary waves propagating all over space-time as given data, we rather consider that it represents the mean value, all over the field, of different varying frequencies Ω(x, t). In other words, the modulation waves with perturbation frequency δΩ(x, t), propagating at light velocity, behave as interactions between main waves, leading that their frequency w remains practically constant all over the space-time.
From a mathematical point of view, almost fields properties derive from monochromatic ones, through the variation of constants method (Duhamel principle). Accordingly, following (10), an almost standing wave obeys,
e(x, t) = U(x, t)expiɸ(x, t) ɸ(x, t) = W(x, t)t − K(x, t)x + 2np, (12)
where products of second order dWdt » 0 and dKdx » 0, defined modulo 2p, are neglected at first order of approximation. This is equivalent to incorporate, in almost monochromatic solutions, the boundary conditions defined by Fourier relations.
dɸ(x, t) = W(x, t)dt − K(x, t)dx » wdt − kdx. U(x, t) = u(x, t) ± dU(x, t) (13)
According to (4), e(x, t) in (12) verifies,
¶m¶mU − U¶mj¶mj = 0 or ¶2U/c2¶t2 − Ñ2U − U[(¶j/c¶t)2 − (Ñj)2] = 0 (14)
¶m(U2¶mj) = 0 or ¶(U2W)/c2¶t + Ñ(U2bK) = 0 (15)
These relations apply to progressive waves for b = ±1, to standing waves at rest for b = 0 and in motion for b < 1, to monochromatic waves for w and k constant, to almost monochromatic waves for varying W(x, t) et K(x, t).
They lead to dynamical properties for energy-momentum conservation, and to least action principles, for standing fields and almost standing fields [9] -[12] .
For a standing wave, either at rest or in motion, the frequency is constant δΩ(x, t) = 0, so that (15) reduces to
¶u02/¶t0 = 0. ¶u2/¶t + Ñu2v = 0 or ¶mwm = 0 (16)
where wm = (u2, u2v/c) = u0(x0)2(1, v/c)/ is a four-dimensional vector. This continuity equation for u2
is a four-dimensional vector. This continuity equation for u2
is formally identical with Newton’s equation continuity for matter-momentum density
¶µ/¶t + ѵv = 0. with u2 = µc2, (17)
We are then led to admit, by transposition, that u2 represents the energy density of the standing field.
Following relations (8) and (9), in the spherical symmetry case, and for its kinematical behavior, the space function u0 can be reduced to its point-like centre of energy density whose position x0 is such that
Ñ0u02 = 0 Ñu2 + (¶u2v/c2¶t) = 0 Ñ × v = 0 or pmn = ¶mwn − ¶nwm = 0, (18)
Since u2 is a standing wave energy density spread in space, and then a potential energy density, −Ñu2 = −ÑwP = F is a density force, and ¶u2v/c2¶t a density momentum. Then pmn is a four-dimensional force density.
Equation (18), where energy density wm is a four-dimensional gradient ¶ma, is mathematically equivalent to the least action relation
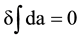
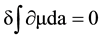 with wm = ¶ma. (19)
with wm = ¶ma. (19)
When transposing the mass density µ = u2/c2, and taking into account the two identities ÑP2 = 2(PÑ)P + 2P ´ (Ñ ´ P) and dP/dt = ¶P/¶t + (vÑ)P for c and v constant, after integration with respect to space, we get the equation for matter
dp/dt = −Ñmc2 + {Ñ(mv)2}/2m dp/dt = ÑLm = −Ñm0c2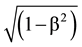 . (20)
. (20)
We retrieve the relativistic Lagrangian of mechanics for free matter Lm = −m0c2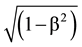 [18] .
[18] .
4.3. Electromagnetism
For of an almost standing wave, the continuity equation applies that the total energy density W = U2W = w + dW, is sum of the mean standing wave w and of the interactions dW. The relations (18) become
Pmn = ¶mWn − ¶nWm = 0 or Pmn = pmn + dPmn = 0 (21)
By difference with the null four-dimensional density force pmn for a standing wave, only the total density force Pmn for an almost standing wave vanishes. In the first case, this asserts the space stability of an isolated standing wave, while in the second case, the space stability concerns the whole almost standing wave. It behaves as a system composed of two sub-systems, the mean standing field with high frequency W(x, t) » w, and the interaction field with low frequency dW(x, t), each one exerting an equal and opposite density force pmn = −dPmn against the other.
In (18), the vanishing four-dimensional force density tensor pmn of a standing wave, asserts that the energy-momentum density four-vector wm is four-parallel, or directed along the motion velocity v. By comparison, for an almost standing wave, the total energy-momentum density tensor Pmn which still vanishes, asserts also that the total energy-momentum density four-vector Wm is four-parallel, or directed along the motion velocity v. However, the mean energy-momentum density tensor pmn, no longer vanishes in (21) as previously in (18): the mean energy-momentum density four-vector wm is then no longer parallel. This comes from the opposite density force dPmn exerted by the interaction.
It appears that an almost standing wave behaves as a whole system in motion which can be split in two sub-systems, the mean standing wave and the interaction field. Both are moving with velocity v, while exerting each other opposite forces in different directions, including perpendicularly to the velocity v. The perturbation field, arising from local frequency variations dW(x, t), introduces orthogonal components in interaction density force and momentum.
The relations (20), generalized by the constants variation method for the mass M(x, t) = m ± dM(x, t), become
ÑMc2 + ¶P/¶t = 0 Ñ × P = 0 dP/dt = −ÑMc2 + (ÑP2)/2M. (22)
The density force dPmn ¹ 0 exerted by the interaction is formally identical with the electromagnetic tensor Fmn = ¶mAn − ¶nAm ¹ 0. We can set them in correspondence dPmn = eFmn, through a constant charge e, in which dM(x, t) = eV(x, t)/c2 and dP(x, t) = eA(x, t)/c. The double sign for mass variation corresponds to the two signs for electric charges, or to emission and absorption of electromagnetic energy by matter. We retrieve the minimum coupling of classical electrodynamics, Pm(x, t) = pm + eAm(x, t)/c, with M(x, t)c2 = mc2 + eV(x, t), and P(x, t) = p + eA(x, t)/c where electromagnetic energy exchanged with a particle is very small with respect to ist own energy eAm(x, t)/c = dPm(x, t) << pm [18] . Electromagnetic interaction is then directly linked to frequencies variations of the field e.
From (22) we derive then the relativistic Newton’s equation for charged matter with the Lorentz force
dP/dt = −Ñm0c2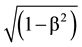 + e(E + v × H/c). (23)
+ e(E + v × H/c). (23)
4.4. Adiabatic Invariance
For an almost standing wave, in place of (16), we get from (13) and (15), to first order approximation,
[¶U2/¶t + ÑU2v]/U2 + d[¶W/¶t + ÑWv]/W = 0 or (¶nWn)/W + d(¶nWn)/W = 0. (24)
where W = w ± dW = µc2 = µc2 ± dµc2 is energy density, Wn = wn ± dWn = (µc2, µvc) four-dimensional energy density, Ω = w ± δΩ the frequency and Wn = (W, Wv/c) the four-dimensional frequency. These relations imply that
W = IW and Wn = IWn (25),
when we take into account the double sign in frequency variation dW. The constant I is an adiabatic invariant density. In first approximation, they reduce to energy-momentum densities, and to their variations, relations
wn = Iwn or µc2 = Iw µv = Ibk (26)
dWn = IdWn or dµc2 = IdW dµv = IdbK (27)
Integrations of µ and I densities with respect to space, lead to relations between four-energy and four-frequency
En = (mc2, pc) = m0c2un = Hwn = H(w, kc) = Hw0un un = (1, v/c) m0c2 = Hw0 (28)
through the adiabatic invariant H. Since the Planck’s constant h behaves as an adiabatic invariant [17] , these relations show h proximity with electromagnetism, more especially as they both lean upon slight frequency variations. However, their rigorous connections remain unsolved since h applies to all particles with different masses, while this does not seem to occur for H, after integration of I with respect to space. Consequently, even if, from historical point of view, Planck’s constant h was introduced in direct connection with electromagnetism, through black-body radiation, these relations pave only the way to a more complete approach.
5. Gravitation and General Relativity
All above, starting from the d’Alembertian Equation (4) for a scalar field e propagating with a constant velocity c in vacuum, we derived almost standing waves properties, characterized in a rest system (x0, t0) by separated space and time variables e0(x0, t0) = u0(k0x0)y0(w0t0), and a constant frequency w0 = k0c. The Lorentz transformation expresses that its stability remains in uniform motion with speed v.
Before its application to mechanics, and more generally to special relativistic physics, the Lorentz transformation determined the structure of Maxwell’s equations in vacuum. The presence of matter, as support of electric charges, modifies locally the field properties, through induced dielectric and magnetic permeability variations, so that the field velocity propagation c is no longer constant, and must be written C(x, t) [19] .
Since localized standing waves behave like matter, we may expect that, as a secondary effect, their energy density u2 = µc2 modifies very slightly the field propagation velocity, so that it remains close to its vacuum constant value, becoming C(x, t) = c ± dC(x, t), with dC(x, t) << c. The relation v = bc shows that the local variations of the motion velocity V(x, t) must follow, leading to V(x, t) = v ± dV(x, t), with dV(x, t) << v. Consequently, the Lorentz transformation (1), in which the velocities v and c are constant, appears as expressing only a local approximation limit, from a more general form with varying velocities. In order to find it, we notice that in the relation w = kc, the varying field velocity c tends toward C(x, t). It leads to varying frequency w and wave vector k in W(x, t) = K(x, t)C(x, t). Then, in a rest system, space and time terms are no longer fully separated in expression e0(x0, t0) = U0(x0, t0)Y0(x0, t0). The invariant interval s2 = c2t02 = c2t2 − x2, takes then the more general local form ds2 = gijdxidxj, introducing the formalism of general relativity, and leading to all its developments and consequences.
However, for almost standing waves, all quantities variations are very slight in comparison with their standing waves constant values. The Lorentz transformation remains locally verified for standing waves, as approximations of almost standing waves, when the velocity of propagation of the field C(x, t) reduces to c.
Inversely, dynamical properties of almost standing waves arise from those of standing waves, through variation of constants method for velocities C and V, while the mass density m = u2/c2 of the standing wave limit remains unaffected in first approximation, according to (13) in the continuity Equation (16) written in the form (20)
d(mV)/dt = −ÑmC2 + Ñ(mV)2/2m mdV/dt = −mÑ(C2 − V2/2) (29)
dV/dt = −Ñ(C(x, t)2 − V(x, t)2/2) dV/dt0 = −Ñ0C2(x0, t0) = −Ñ0F(x0, t0). (30)
The acceleration of an almost standing wave, either at rest or in motion, is locally independent of its energy density, equivalent to mass density of matter. This characterizes gravitation interaction [18] . The gravitational potential F(x, t) = C2(x, t) is formally identical with the square of the local velocity of propagation of the field.
The relations (29) are consistent with physical origin of gravitation, exposed in 1912 by Einstein, in a preliminary article on general relativity of 1915, on Light velocity and static gravitation field, [20] . He established the equation Dc = 0 in vacuum, generalizing the Poisson equation DF = 0 for the gravitation potential.
6. Gravitation and Electromagnetism Conciliation
By integration of mass density m all over space, the relation (26) leads to general classical equation [7]
dP/dt = −ÑMC2 + Ñ(MV)2/2M. then E0 = M0(x0, t0)C2(x0, t0) = constant (31)
when the mass M is constant, the variations of velocities, C of the field, and V of the matter, lead to the gravitation force in (28), and to the gravitational Lagrangian LG = −MF(x, t) + Mv2/2, in an inertial frame of relativistic mechanics, which remains locally valid in general relativity [18] . When the velocities C of the field and V of the matter are constant, the variations dM(x, t) = eV(x, t)/c2 of the mass M derive from electromagnetic interactions, leading to the relativistic mechanical Lagrangian of charged matter
dP/dt = −MÑ(C2 − V2/2) − (C2 − V2)ÑM = −ÑLG − ÑLm = −ÑL. (32)
The total Lagrangian L, is then the sum of gravitational LG and charged mechanical Lm Lagrangians.
dE0 = d(M0C2) = M0dC2 + C2dM0 = dEG + dEm dEn = dEnG + dEnm (33)
For matter at rest, and in uniform motion, interaction energies of electromagnetic charged matter dEm and of gravitation dEG , derive from its total energy E0 = M0C2. However, contrarily to gravitation, only electromagnetic energy is quantified dEm = hdW, according to (28).
7. Concluding Remarks
Following Einstein’s program, founded on a scalar field propagating at speed of light, one can derive main physical properties of matter and of gravitational and electromagnetic interactions. Matter corresponds to standing waves, while interactions correspond to progressive waves. When frequencies are infinitely high, they render oscillations inaccessible with time, since they are too rapid, and inaccessible with space, since the wavelengths are too small. Only mean effects appear. Physical phenomena exhibit then, theoretically and experimentally, as particles. Classical relativist equations of mechanics correspond to geometrical optics approximation.
In mechanics and electromagnetism domains, the very slight local variations, or local adiabatic variations, of almost standing waves frequency, lead to variations of energy density, or to equivalent mass density, while the field velocity c and motion velocity v = dx/t, are locally constant. The underlying invariance structure with respect to motion, is expressed by local Lorentz tranformation, with invariant interval ds2 = c2dt02 = c2dt2 − dx2.
We retrieve then the main classical relativist relations for matter, such as the variational principle and the energy-momentum conservation laws, and particularly its energy E = mc2. The variations of frequencies lead to the quantum relation E = hν for matter (second quantification), and dE = hdν for electromagnetic interaction (first quantification), as well as to Fourier relations, homogeneous to the field, leading to the Heisenberg relations, homogeneous to matter. They lead also to an interaction which is formally identical with electromagnetism.
The variations of light velocity lead to an interaction, formally identical with gravitation. In gravitational domain, the whole equivalent mass of an almost standing wave, or the total mass of matter, including interaction energy, is submitted to local variations of the field velocity C(x, t) and of motion velocity V(x, t). The underlying invariance structure with respect to motion, is expressed by the local invariant interval ds2 = gijdxi dxj, of general relativity.
The Einstein’s program permits to conciliate gravitation and electromagnetism. Since they act as interactions of matter, both derive from variations of its energy E = mc2: electromagnetism from mass m variation, and gravitation from light velocity c variation. Electromagnetism alone, but not gravitation, derives from the frequency ν variation of the matter energy E = hν = mc2, leading to its quantification.
This would get an insight into theoretical difficulties encountered to incorporate gravitation in standard model of particles, and into experimental difficulties to detect the graviton as mediating quantum particle.