1. Introduction
After a thorough discussion of the terminology used in this article, such as the logarithmic and power form of abelian type invariants in Section 2, and multilayered transfer target types (TTTs), ordered and accumulated index-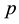 abelianization data (IPADs) up to the third order in Section 3, we state the main results on IPADs of exceptional form in Section 3.1, and on IPADs in parametrized infinite sequences in Section 3.2. These main theorems give all possible IPADs of number fields
abelianization data (IPADs) up to the third order in Section 3, we state the main results on IPADs of exceptional form in Section 3.1, and on IPADs in parametrized infinite sequences in Section 3.2. These main theorems give all possible IPADs of number fields  with 3-class group
with 3-class group  of type
of type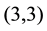 .
.
Before we turn to applications in extreme computing, that is, squeezing the computational algebra systems PARI/GP [1] and MAGMA [2] -[4] to their limits in Section 5, where we show how to detect malformed IPADs in Section 5.1, and how to complete partial 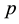 -capitulation types in Section 5.2, we have to establish a com- ponentwise correspondence between transfer kernel types (TKTs) and IPADs in Section 4 by exploiting details of proofs which were given in [5] .
-capitulation types in Section 5.2, we have to establish a com- ponentwise correspondence between transfer kernel types (TKTs) and IPADs in Section 4 by exploiting details of proofs which were given in [5] .
Iterated IPADs of second order are used in Section 6 for the indirect calculation of TKTs in Section 6.1, and for determining the exact length 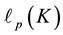 of the
of the 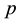 -class tower of a number field K in Section 6.2. These
-class tower of a number field K in Section 6.2. These
sophisticated techniques prove  for quadratic number fields
for quadratic number fields  with
with
 (the first real quadratic fields) and
(the first real quadratic fields) and 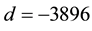 (the first tough complex quadratic field after the easy
(the first tough complex quadratic field after the easy 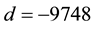 ( [6] , Cor.4.1.1), which resisted all attempts up to now.
( [6] , Cor.4.1.1), which resisted all attempts up to now.
Finally, we emphasize that IPADs of infinite ![]() -class towers reveal an unknown wealth of possible fine structure in Section 7 on complex quadratic fields
-class towers reveal an unknown wealth of possible fine structure in Section 7 on complex quadratic fields ![]() having a 3-class group
having a 3-class group ![]() of type
of type![]() .
.
2. Abelian Type Invariants
Let ![]() be a prime number and
be a prime number and ![]() be a finite abelian
be a finite abelian ![]() -group. According to the main theorem on finitely generated abelian groups, there exists a non-negative integer
-group. According to the main theorem on finitely generated abelian groups, there exists a non-negative integer![]() , the rank of
, the rank of![]() , and a sequence
, and a sequence ![]() of positive integers such that
of positive integers such that ![]() and
and
![]() (1)
(1)
The powers![]() ,
, ![]() , are known as the elementary divisors of
, are known as the elementary divisors of![]() , since
, since ![]() for each
for each![]() . It is convenient to collect equal elementary divisors in formal powers with positive exponents
. It is convenient to collect equal elementary divisors in formal powers with positive exponents ![]() such that
such that![]() ,
, ![]() , and
, and
![]()
The cumbersome subscripts can be avoided by defining ![]() for each
for each![]() . Then
. Then
![]() (2)
(2)
and we can define:
Definition 2.1. The abelian type invariants (ATI) of ![]() are given by the sequence
are given by the sequence
![]() (3)
(3)
of strictly increasing positive integers ![]() with multiplicities
with multiplicities ![]() written as formal exponents indicating iteration.
written as formal exponents indicating iteration.
Remark 2.1. The integers ![]() are the
are the ![]() -logarithms of the elementary divisors
-logarithms of the elementary divisors![]() .
.
1) For abelian type invariants of high complexity, the logarithmic form in Definition 2.1 requires considerably less space (e.g. in Section 7, Table 2) than the usual power form
![]() (4)
(4)
2) For brevity, we can even omit the commas separating the entries of the logarithmic form of abelian type invariants, provided all the ![]() remain smaller than 10.
remain smaller than 10.
3) A further advantage of the brief logarithmic notation is the independence of the prime![]() , in particular when
, in particular when ![]() -groups with distinct
-groups with distinct ![]() are being compared.
are being compared.
4) Finally, since our preference is to select generators of finite ![]() -groups with decreasing orders, we agree to write abelian type invariants from the right to the left, in both forms.
-groups with decreasing orders, we agree to write abelian type invariants from the right to the left, in both forms.
Example 2.1. For instance, if![]() , then the abelian type invariants
, then the abelian type invariants ![]() in logarithmic form corre- spond to the power form
in logarithmic form corre- spond to the power form ![]() and
and ![]() corresponds to
corresponds to![]() .
.
Now let ![]() be an arbitrary finite
be an arbitrary finite ![]() -group or infinite topological pro-
-group or infinite topological pro-![]() group with derived subgroup
group with derived subgroup ![]() and finite abelianization
and finite abelianization![]() .
.
Definition 2.2. The abelian type invariants of the commutator quotient group ![]() are called the abelian quotient invariants (AQI) of
are called the abelian quotient invariants (AQI) of![]() , that is,
, that is,![]() .
.
3. Index-p Abelianization Data
Let ![]() be a fixed prime number and
be a fixed prime number and ![]() be a number field with
be a number field with ![]() -class group
-class group ![]() of order
of order![]() , where
, where ![]() denotes a non-negative integer.
denotes a non-negative integer.
According to the Artin reciprocity law of class field theory [7] , ![]() is isomorphic to the commutator
is isomorphic to the commutator
quotient group ![]() of the Galois group
of the Galois group ![]() of the maximal unramified pro-
of the maximal unramified pro-![]()
extension ![]() of
of![]() .
. ![]() is called the
is called the ![]() -class tower group (briefly
-class tower group (briefly ![]() -tower group) of
-tower group) of![]() . The fixed field of the commutator subgroup
. The fixed field of the commutator subgroup ![]() in
in ![]() is the maximal abelian unramified
is the maximal abelian unramified ![]() -extension of
-extension of![]() , that is the (first) Hilbert
, that is the (first) Hilbert ![]() -class field
-class field ![]() of
of ![]() with Galois group
with Galois group
![]() . The derived subgroup
. The derived subgroup ![]() is a closed (and
is a closed (and
open) subgroup of finite index ![]() in the topological pro-
in the topological pro-![]() group
group![]() .
.
Definition 3.1. For each integer![]() , the system
, the system
![]() (5)
(5)
of intermediate fields ![]() with relative degree
with relative degree ![]() is called the
is called the ![]() -th layer of abelian un-ramified
-th layer of abelian un-ramified ![]() -extensions of
-extensions of![]() . In particular, for
. In particular, for![]() ,
, ![]() forms the bottom layer
forms the bottom layer![]() , and for
, and for![]() ,
, ![]() forms the top layer
forms the top layer![]() .
.
Now let ![]() be a fixed integer and suppose that
be a fixed integer and suppose that ![]() belongs to the
belongs to the ![]() -th layer. Then the
-th layer. Then the
Galois group ![]() is of finite index
is of finite index ![]() in the
in the ![]() -tower group
-tower group ![]() of
of ![]()
and the quotient ![]() is abelian, since
is abelian, since ![]() contains the commutator subgroup
contains the commutator subgroup
![]() of.
of.
Definition 3.2. For each integer![]() , the system
, the system
![]() (6)
(6)
of intermediate groups ![]() with index
with index ![]() is called the
is called the ![]() -th layer of normal subgroups of
-th layer of normal subgroups of ![]() with abelian quotients
with abelian quotients![]() . In particular, for
. In particular, for![]() ,
, ![]() forms the top layer
forms the top layer![]() , and for n = v,
, and for n = v, ![]() forms the bottom layer
forms the bottom layer![]() .
.
A further application of Artin’s reciprocity law [7] shows that
![]() (7)
(7)
for every subgroup ![]() and its corresponding extension field
and its corresponding extension field![]() , where
, where ![]() is fixed (but arbitrary).
is fixed (but arbitrary).
Since the abelianization ![]() forms the target of the Artin transfer homomorphism
forms the target of the Artin transfer homomorphism ![]() from G to H [8] , we introduced a preliminary instance of the following terminology in ( [9] , Dfn. 1.1, p. 403).
from G to H [8] , we introduced a preliminary instance of the following terminology in ( [9] , Dfn. 1.1, p. 403).
Definition 3.3. For each integer![]() , the multiplet
, the multiplet![]() , where each member
, where each member ![]() is interpreted rather as its abelian type invariants, is called the
is interpreted rather as its abelian type invariants, is called the ![]() -th layer of the transfer target type (TTT) of the pro-
-th layer of the transfer target type (TTT) of the pro-![]() group
group![]() ,
,
![]() (8)
(8)
Similarly, the multiplet![]() , where each member
, where each member ![]() is interpreted rather as its
is interpreted rather as its
abelian type invariants, is called the ![]() -th layer of the transfer target type (TTT) of the number field
-th layer of the transfer target type (TTT) of the number field![]() ,
,
![]() (9)
(9)
Remark 3.1.
1) If it is necessary to specify the underlying prime number![]() , then the symbol
, then the symbol![]() , resp.
, resp.![]() , can be used for the TTT.
, can be used for the TTT.
2) Suppose that![]() . If an ordering is defined for the elements of
. If an ordering is defined for the elements of![]() , resp.
, resp.![]() , then the same ordering is applied to the members of the layer
, then the same ordering is applied to the members of the layer![]() , resp.
, resp.![]() , and the TTT layer is called ordered. Otherwise, the TTT layer is called unordered or accumulated, since equal components are collected in powers with formal exponents denoting iteration.
, and the TTT layer is called ordered. Otherwise, the TTT layer is called unordered or accumulated, since equal components are collected in powers with formal exponents denoting iteration.
3) In view of the considerations in Equation (7), it is clear that we have the equality
![]() (10)
(10)
in the sense of componentwise isomorphisms.
Since it is increasingly difficult to compute the structure of the ![]() -class groups
-class groups ![]() of extension fields
of extension fields ![]() in higher layers with
in higher layers with![]() , it is frequently sufficient to make use of information in the first layer only, that is the layer of subgroups with index
, it is frequently sufficient to make use of information in the first layer only, that is the layer of subgroups with index![]() . Therefore, Boston, Bush and Hajir [10] invented the following first order approximation of the TTT, a concept which had been used in earlier work already [11] - [15] , without explicit terminology.
. Therefore, Boston, Bush and Hajir [10] invented the following first order approximation of the TTT, a concept which had been used in earlier work already [11] - [15] , without explicit terminology.
Definition 3.4. The restriction
![]() (11)
(11)
of the TTT![]() , resp.
, resp.![]() , to the zeroth and first layer is called the index-
, to the zeroth and first layer is called the index-![]() abelianization data (IPAD) of
abelianization data (IPAD) of![]() , resp.
, resp.![]() .
.
So, the complete TTT is an extension of the IPAD. However, there also exists another extension of the IPAD which is not covered by the TTT. It has also been used already in previous investigations by Boston, Bush and Nover [12] [14] [15] and is constructed from the usual IPAD ![]() of
of![]() , firstly, by observing that
, firstly, by observing that
![]() can be viewed as
can be viewed as ![]() and, secondly, by extending each
and, secondly, by extending each ![]()
to the IPAD ![]() of
of![]() .
.
Definition 3.5. The family
![]() (12)
(12)
is called the iterated IPAD of second order of![]() , resp.
, resp.![]() .
.
The concept of iterated IPADs as given in Dfn. 3.5 is restricted to the second order and first layers, and thus is open for further generalization (higher orders and higher layers). Since it could be useful for 2-power extensions, whose absolute degrees increase moderately and remain manageable by MAGMA [4] or PARI/GP [1] , we briefly indicate how the iterated IPAD of third order could be defined:
![]() (13)
(13)
3.1. Sporadic IPADs
In the next two central theorems, we present complete specifications of all possible IPADs of pro-![]() groups
groups ![]() for
for ![]() in the simplest case of an abelianization
in the simplest case of an abelianization ![]() of type
of type![]() . We start with pro-3 groups
. We start with pro-3 groups ![]() whose metabelianizations
whose metabelianizations ![]() are vertices on sporadic parts of coclass graphs outside of coclass trees ( [9] , Section 2, p. 410), ( [16] Section 10).
are vertices on sporadic parts of coclass graphs outside of coclass trees ( [9] , Section 2, p. 410), ( [16] Section 10).
Since the abelian type invariants of the members of TTT layers will depend on the parity of the nilpotency class ![]() or coclass
or coclass![]() , a more economic notation, avoiding the tedious distinction of the cases odd or even, is provided by the following definition ( [5] , Section 3).
, a more economic notation, avoiding the tedious distinction of the cases odd or even, is provided by the following definition ( [5] , Section 3).
Definition 3.6. For an integer![]() , the nearly homocyclic abelian 3-group
, the nearly homocyclic abelian 3-group ![]() of order
of order ![]() is de- fined by its type invariants
is de- fined by its type invariants![]() , where the quotient
, where the quotient ![]() and the remainder
and the remainder ![]() are determined uniquely by the Euclidean division
are determined uniquely by the Euclidean division![]() . Two degenerate cases are included by putting
. Two degenerate cases are included by putting ![]() the cyclic group
the cyclic group ![]() of order 3 and
of order 3 and ![]() the trivial group of order 1.
the trivial group of order 1.
In the following theorems, we use the identifiers in the SmallGroups Library [17] [18] .
Theorem 3.1. (First Main Theorem on![]() ,
, ![]() , and
, and ![]() of small class)
of small class)
Let ![]() be a pro-3 group having a transfer target type
be a pro-3 group having a transfer target type ![]() with top layer com- ponent
with top layer com- ponent![]() . Let
. Let ![]() denote the defect of commutativity ([9] , 3.1.1, p.412, and 3.3.2, p. 429) of the metabelianization
denote the defect of commutativity ([9] , 3.1.1, p.412, and 3.3.2, p. 429) of the metabelianization ![]() of
of![]() . Then the ordered first layer
. Then the ordered first layer ![]() and the bottom layer
and the bottom layer ![]() are given in the following way (exceptional cases in boldface font).
are given in the following way (exceptional cases in boldface font).
1) If ![]() is of coclass
is of coclass ![]() and nilpotency class
and nilpotency class![]() , then
, then
![]() (14)
(14)
where generally![]() .
.
2) If ![]() is of coclass
is of coclass ![]() and nilpotency class
and nilpotency class![]() , then
, then
![]() (15)
(15)
where ![]() can be warranted for
can be warranted for ![]() only.
only.
However, if ![]() with
with![]() , then
, then
![]() (16)
(16)
3) If ![]() is of coclass
is of coclass ![]() and nilpotency class
and nilpotency class![]() , then
, then
![]() (17)
(17)
However, if![]() , then
, then
![]() (18)
(18)
where the irregular case can only occur for even class and coclass![]() , positive defect of commutativity
, positive defect of commutativity![]() , and relational parameter
, and relational parameter ![]() in ([5] , Equation (3.6), p. 424) or ( [9] , Equation (3.3), p. 430).
in ([5] , Equation (3.6), p. 424) or ( [9] , Equation (3.3), p. 430).
Proof. Since this proof heavily relies on our earlier paper [5] , it should be pointed out that, for a ![]() -group
-group![]() , the index of nilpotency
, the index of nilpotency ![]() is used generally instead of the nilpotency class
is used generally instead of the nilpotency class ![]() and the invariant
and the invariant ![]() frequently (but not always) replaces the coclass
frequently (but not always) replaces the coclass ![]() in that paper.
in that paper.
1) Using the association between the identifier of ![]() in the SmallGroups Library [17] [18] and the transfer kernel type (TKT) [19] , which is visualized in ([5] , Figure 3.1, p. 423) and ( [16] , Figure 3), this claim follows from ([5] , Thm. 4.1, p. 427, and Tbl. 4.1, p. 429).
in the SmallGroups Library [17] [18] and the transfer kernel type (TKT) [19] , which is visualized in ([5] , Figure 3.1, p. 423) and ( [16] , Figure 3), this claim follows from ([5] , Thm. 4.1, p. 427, and Tbl. 4.1, p. 429).
2) For![]() , resp.
, resp. ![]() with
with![]() , the statement is a consequence of ([5] , Thm. 4.2 and Tbl. 4.3, p. 434), resp. ([5] , Thm. 4.3 and Tbl. 4.5, p. 438), when the association between the identifier of
, the statement is a consequence of ([5] , Thm. 4.2 and Tbl. 4.3, p. 434), resp. ([5] , Thm. 4.3 and Tbl. 4.5, p. 438), when the association between the identifier of ![]() in the SmallGroups database and the TKT is taken into consideration, as visualized in ([5] , Figure 4.1, p. 433) and ( [16] , Figure 4).
in the SmallGroups database and the TKT is taken into consideration, as visualized in ([5] , Figure 4.1, p. 433) and ( [16] , Figure 4).
3) All the regular cases behave completely similar as the general case in Theorem 3.2, item (3), Equation (22). In the irregular case, only the bottom layer![]() , consisting of the abelian quotient invariants
, consisting of the abelian quotient invariants ![]() of the derived subgroup
of the derived subgroup![]() , is exceptional and must be taken from ( [5] , Appendix 8, Thm. 8.8, p.461). □
, is exceptional and must be taken from ( [5] , Appendix 8, Thm. 8.8, p.461). □
3.2. Infinite IPAD Sequences
Now we come to the IPADs of pro-![]() groups
groups ![]() whose metabelianizations
whose metabelianizations ![]() are members of infinite periodic sequences, inclusively mainlines, of coclass trees.
are members of infinite periodic sequences, inclusively mainlines, of coclass trees.
Theorem 3.2. (Second Main Theorem on![]() ,
, ![]() , and
, and ![]() of large class)
of large class)
Let ![]() be a pro-3 group having a transfer target type
be a pro-3 group having a transfer target type ![]() with top layer com- ponent
with top layer com- ponent![]() . Let
. Let ![]() denote the defect of commutativity ( [9] , Section 3.1.1, p. 412, and Section 3.3.2, p. 429) of the metabelianization
denote the defect of commutativity ( [9] , Section 3.1.1, p. 412, and Section 3.3.2, p. 429) of the metabelianization ![]() of
of![]() . Then the ordered first layer
. Then the ordered first layer ![]() and the bottom layer
and the bottom layer ![]() are given in the following way.
are given in the following way.
1) If ![]() is of coclass
is of coclass ![]() and nilpotency class
and nilpotency class![]() , then
, then
![]() (19)
(19)
2) If ![]() is of coclass
is of coclass ![]() and nilpotency class
and nilpotency class![]() , or c = 4 with
, or c = 4 with![]() , then
, then
![]() (20)
(20)
in dependence on the coclass tree![]() ,
, ![]() , but uniformly
, but uniformly
![]() (21)
(21)
3) If ![]() is of coclass
is of coclass ![]() and nilpotency class
and nilpotency class![]() , or
, or ![]() with
with![]() , then
, then
![]() (22)
(22)
The first member ![]() of the ordered first layer
of the ordered first layer ![]() reveals a uni-polarization (dependence on the nilpotency class
reveals a uni-polarization (dependence on the nilpotency class![]() ), whereas the other three members
), whereas the other three members![]() ,
, ![]() , show a stabilization (independence of
, show a stabilization (independence of![]() ) for fixed coclass
) for fixed coclass![]() .
.
Proof. Again, we make use of [5] , and we point out that, for a ![]() -group G, the index of nilpotency
-group G, the index of nilpotency ![]() is used generally instead of the nilpotency class
is used generally instead of the nilpotency class ![]() and the invariant
and the invariant ![]() frequently (but not always) replaces the coclass
frequently (but not always) replaces the coclass ![]() in that paper.
in that paper.
1) All components of ![]() are given in ([5] , Section 3.1, Thm. 3.1, Equation (3.4)-(3.5), p. 421) when their ordering is defined by the special selection of generators ([5] , Section 3.1, Equation (3.1)-(3.2), p. 420). There is only a unique coclass tree with 3-groups of coclass 1.
are given in ([5] , Section 3.1, Thm. 3.1, Equation (3.4)-(3.5), p. 421) when their ordering is defined by the special selection of generators ([5] , Section 3.1, Equation (3.1)-(3.2), p. 420). There is only a unique coclass tree with 3-groups of coclass 1.
2) The first component of ![]() is given in ([5] , Section 3.2, Thm.3.2, Equation (3.7), p. 424), and the last three components of
is given in ([5] , Section 3.2, Thm.3.2, Equation (3.7), p. 424), and the last three components of ![]() are given in ([5] , Section 4.5, Thm. 4.4, p. 440) and ([5] , Section 4.5, Tbl. 4.7, p. 441), when their ordering is defined by the special selection of generators ([5] , Section 3.2, Equation (3.6), p. 424). The invariant
are given in ([5] , Section 4.5, Thm. 4.4, p. 440) and ([5] , Section 4.5, Tbl. 4.7, p. 441), when their ordering is defined by the special selection of generators ([5] , Section 3.2, Equation (3.6), p. 424). The invariant ![]() ([5] , Section 4, p. 426), which counts IPAD components of rank 3, decides to which of the mentioned three coclass trees the group
([5] , Section 4, p. 426), which counts IPAD components of rank 3, decides to which of the mentioned three coclass trees the group ![]() belongs ( [9] , Figure 3.6-3.7, pp. 442-443).
belongs ( [9] , Figure 3.6-3.7, pp. 442-443).
3) The first two components of ![]() are given in ([5] , Section 3.2, Thm.3.2, Equation (3.7)-(3.8), p. 424), and the last two components of
are given in ([5] , Section 3.2, Thm.3.2, Equation (3.7)-(3.8), p. 424), and the last two components of ![]() are given in ([5] , Section 4.6, Thm. 4.5, p. 444), when their ordering is defined by the special selection of generators ([5] , Section 3.2, Equation (3.6), p. 424). For coclass bigger than 2, it is irrelevant to which of the four (in the case of odd coclass
are given in ([5] , Section 4.6, Thm. 4.5, p. 444), when their ordering is defined by the special selection of generators ([5] , Section 3.2, Equation (3.6), p. 424). For coclass bigger than 2, it is irrelevant to which of the four (in the case of odd coclass![]() ) or six (in the case of even coclass
) or six (in the case of even coclass![]() ) coclass trees the group
) coclass trees the group ![]() belongs. The IPAD is independent of this detailed information, provided that
belongs. The IPAD is independent of this detailed information, provided that![]() .
.
Finally, the bottom layer![]() , consisting of the abelian quotient invariants
, consisting of the abelian quotient invariants ![]() of the derived sub- group
of the derived sub- group![]() , is generally taken from ([5] , Appendix 8, Thm. 8.8, p. 461). □
, is generally taken from ([5] , Appendix 8, Thm. 8.8, p. 461). □
4. Componentwise Correspondence of IPAD and TKT
Within this section, where generally![]() , we employ some special terminology.
, we employ some special terminology.
Definition 4.1. We say a class of a base field ![]() remains resistant if it does not capitulate in any unramified cyclic cubic extension
remains resistant if it does not capitulate in any unramified cyclic cubic extension![]() .
.
When the 3-class group of ![]() is of type
is of type ![]() the next layer of unramified abelian extensions is already the top layer consisting of the Hilbert 3-class field
the next layer of unramified abelian extensions is already the top layer consisting of the Hilbert 3-class field![]() , where a resistant class must capitulate, according to the Hilbert/Artin/Furtwängler principal ideal theorem [8] .
, where a resistant class must capitulate, according to the Hilbert/Artin/Furtwängler principal ideal theorem [8] .
Our desire is to show that the components of the ordered IPAD and TKT [9] [19] are in a strict corre- spondence to each other. For this purpose, we exploit details of the proofs given in [5] , where generators of metabelian 3-groups G with ![]() were selected in a canonical way, particularly adequate for theore- tical aspects ([5] , Section 3.2, p. 424), ( [9] , Section 3.3.2, p. 429).
were selected in a canonical way, particularly adequate for theore- tical aspects ([5] , Section 3.2, p. 424), ( [9] , Section 3.3.2, p. 429).
Since we now prefer a more computational aspect, we translate the results into a form which is given by the computational algebra system MAGMA [4] .
To be specific, we choose the vertices of two important coclass trees for illustrating these peculiar techniques. The vertices of depth (distance from the mainline) at most 1 of both coclass trees, with roots ![]() and
and ![]() ( [9] , Figure 3.6-3.7, pp. 442-443), are metabelian 3-groups
( [9] , Figure 3.6-3.7, pp. 442-443), are metabelian 3-groups ![]() with order
with order![]() , nilpotency class
, nilpotency class![]() , and fixed coclass
, and fixed coclass![]() .
.
4.1. The Coclass Tree ![]()
Remark 4.1. The first layers of the TTT and TKT of vertices of depth at most 1 of the coclass tree ![]() ( [9] , Figure 3.6, p. 442) consist of four components each, and share the following common properties with respect to Magma’s selection of generators:
( [9] , Figure 3.6, p. 442) consist of four components each, and share the following common properties with respect to Magma’s selection of generators:
1) polarization (dependence on the class![]() ) at the first component of TTT and TKT,
) at the first component of TTT and TKT,
2) Stabilization (independence of the class![]() ) at the last three components,
) at the last three components,
3) Rank 3 at the second TTT component (![]() in [5] ).
in [5] ).
Using the class![]() , resp. an asterisk, as wildcard characters, these common properties can be summarized as follows, now including the details of the stabilization:
, resp. an asterisk, as wildcard characters, these common properties can be summarized as follows, now including the details of the stabilization:
![]() (23)
(23)
However, to assure the general applicability of the theorems and corollaries in this section, we aim at in- dependency of the selection of generators (and thus invariance under permutations).
Theorem 4.1. (in field theoretic terminology)
1) The class associated with the polarization becomes principal in the extension with rank 3.
2) The class associated with rank 3 becomes principal in both extensions of type![]() , in particular,
, in particular, ![]() cannot be a permutation and can have at most one fixed point.
cannot be a permutation and can have at most one fixed point.
In the sequel, we use designations of special TKTs which were developed in [19] - [21] .
Remark 4.2. Aside from the common properties, there also arise variations due to the polarization, which we first express with respect to Magma’s selection of generators:
1) The TKT is E.6, ![]() , if and only if the polarized extension reveals a fixed point principa- lization.
, if and only if the polarized extension reveals a fixed point principa- lization.
2) The TKT is E.14, ![]() , if and only if one of the classes associated with type
, if and only if one of the classes associated with type ![]() becomes principal in the polarized extension.
becomes principal in the polarized extension.
3) The TKT is H.4, ![]() , if and only if the class associated with rank 3 becomes principal in the polarized extension.
, if and only if the class associated with rank 3 becomes principal in the polarized extension.
4) The TKT is c.18, ![]() , if and only if the polarized extension reveals a total principalization (indicated by 0).
, if and only if the polarized extension reveals a total principalization (indicated by 0).
Corollary 4.1. (in field theoretic terminology)
1) For the TKTs E.6 and H.4, both classes associated with type ![]() remain resistant, for TKT E.14 only one of them.
remain resistant, for TKT E.14 only one of them.
2) All extensions satisfy Taussky’s condition (B) [22] , with the single exception of the polarized extension in the case of TKT E.6 or c.18, which satisfies condition (A).
3) TKT E.6 has a single fixed point, E.14 contains a 3-cycle, and H.4 contains a 2-cycle.
Proof. (of Theorem 4.1 and Corollary 4.1)
Observe that in [5] , the index of nilpotency ![]() and the invariant
and the invariant ![]() are used rather than the nilpotency class
are used rather than the nilpotency class ![]() and the coclass
and the coclass![]() . The claims are a consequence of ([5] , 4.5, Tbl. 4.7, p. 441), when we perform a transformation from the first layer TKT and TTT
. The claims are a consequence of ([5] , 4.5, Tbl. 4.7, p. 441), when we perform a transformation from the first layer TKT and TTT
![]()
with respect to the canonical generators, to the corresponding invariants
![]()
with respect to Magma’s generators. □
4.2. The Coclass Tree ![]()
Remark 4.3. The first layer TTT and TKT of vertices of depth at most 1 of the coclass tree ![]() ( [9] , Figure 3.7, p. 443) consist of four components each, and share the following common properties with respect to Magma’s choice of generators:
( [9] , Figure 3.7, p. 443) consist of four components each, and share the following common properties with respect to Magma’s choice of generators:
1) polarization (dependence on the class![]() ) at the second component of TTT and TKT,
) at the second component of TTT and TKT,
2) stabilization (independence of the class![]() ) at the other three components,
) at the other three components,
3) rank 3 does not occur at any TTT component (![]() in [5] ).
in [5] ).
Using the class![]() , resp. an asterisk, as wildcard characters, the common properties can be summarized as follows, now including details of the stabilization:
, resp. an asterisk, as wildcard characters, the common properties can be summarized as follows, now including details of the stabilization:
![]() (24)
(24)
Again, we have to ensure the general applicability of the following theorem and corollary, which must be in- dependent of the choice of generators (and thus invariant under permutations).
Theorem 4.2. (in field theoretic terminology)
1) Two extensions of type (21) reveal fixed point principalization satisfying condition (A) [22] .
2) The remaining extension of type (21) satisfies condition (B), since the class associated with the polarization becomes principal there.
Remark 4.4. Next, we come to variations caused by the polarization, which we now express with respect to Magma’s choice of generators:
1) The TKT is E.8, ![]() , if and only if the polarized extension reveals a fixed point principa- lization.
, if and only if the polarized extension reveals a fixed point principa- lization.
2) The TKT is E.9, ![]() , if and only if one of the classes associated with fixed points becomes principal in the polarized extension.
, if and only if one of the classes associated with fixed points becomes principal in the polarized extension.
3) The TKT is G.16, ![]() , if and only if the class associated with type (21), satisfying con- dition (B), becomes principal in the polarized extension.
, if and only if the class associated with type (21), satisfying con- dition (B), becomes principal in the polarized extension.
4) The TKT is c.21, ![]() , if and only if the polarized extension reveals a total principalization (indicated by 0).
, if and only if the polarized extension reveals a total principalization (indicated by 0).
Corollary 4.2. (in field theoretic terminology)
1) For the TKTs E.8 and E.9, the class associated with type (21), satisfying condition (B), remains resistant.
2) The polarized extension satisfies condition (B) [22] in the case of TKT E.9 or G.16, and it satisfies con- dition (A) in the case of TKT E.8 or c.21.
3) TKT G.16 is a permutation containing a 2-cycle, and TKT E.8 is the unique TKT possessing three fixed points.
Proof. (of Theorem 4.2 and Corollary 4.2)
In our paper [5] , the index of nilpotency ![]() and the invariant
and the invariant ![]() are used rather than the nil- potency class
are used rather than the nil- potency class ![]() and the coclass
and the coclass![]() . All claims are a consequence of ([5] , 4.5, Tbl. 4.7, p. 441), provided we perform a transformation from the first layer TKT and TTT
. All claims are a consequence of ([5] , 4.5, Tbl. 4.7, p. 441), provided we perform a transformation from the first layer TKT and TTT
![]()
with respect to the canonical generators, to the corresponding invariants
![]()
with respect to Magma’s generators. □
5. Applications in Extreme Computing
5.1. Application 1: Sifting Malformed IPADs
Definition 5.1. An IPAD with bottom layer component ![]() is called malformed if it is not covered by Theorems 3.1 and 3.2.
is called malformed if it is not covered by Theorems 3.1 and 3.2.
To verify predicted asymptotic densities of maximal unramified pro-3 extensions in the article [10] numeri- cally, the IPADs of all complex quadratic fields ![]() with discriminants
with discriminants ![]() and 3-class rank
and 3-class rank ![]() were computed by Boston, Bush and Hajir with the aid of PARI/GP [1] . In particular, there occurred 276375, resp. 122444, such fields with 3-class group
were computed by Boston, Bush and Hajir with the aid of PARI/GP [1] . In particular, there occurred 276375, resp. 122444, such fields with 3-class group ![]() of type
of type![]() , resp.
, resp.![]() .
.
Example 5.1.
A check of all 276375 IPADs for complex quadratic fields with type ![]() in the range
in the range ![]() of discriminants, for which Theorem 3.2 states that the 3-class groups of the 4 unramified cyclic cubic extensions can only have 3-rank 2, except for the unique type
of discriminants, for which Theorem 3.2 states that the 3-class groups of the 4 unramified cyclic cubic extensions can only have 3-rank 2, except for the unique type![]() , revealed that the following 5 IPADs were com- puted erroneously by the used version of PARI/GP [1] in [10] . The successful recomputation was done with MAGMA [4] .
, revealed that the following 5 IPADs were com- puted erroneously by the used version of PARI/GP [1] in [10] . The successful recomputation was done with MAGMA [4] .
1) For d = −96174803, the erroneous IPAD ![]() contained the mal-
contained the mal-
formed component ![]() instead of the correct
instead of the correct![]() . The transfer kernel type (TKT) [9] [19] [21] turned out to be F.12.
. The transfer kernel type (TKT) [9] [19] [21] turned out to be F.12.
2) For![]() , the erroneous IPAD
, the erroneous IPAD ![]() contained the
contained the
malformed component ![]() instead of the correct
instead of the correct![]() . Its TKT is H.4.
. Its TKT is H.4.
3) For![]() , the erroneous IPAD
, the erroneous IPAD ![]() contained the mal-
contained the mal-
formed component ![]() instead of the correct
instead of the correct![]() . The TKT is D.10.
. The TKT is D.10.
4) For![]() , the erroneous IPAD
, the erroneous IPAD ![]() contained the mal-
contained the mal-
formed component ![]() instead of the correct
instead of the correct![]() . This could be a TKT E.8 or E.9 or G.16.
. This could be a TKT E.8 or E.9 or G.16.
5) For![]() , the erroneous IPAD
, the erroneous IPAD ![]() contained the
contained the
malformed component ![]() instead of the correct
instead of the correct![]() . This could be a TKT E.6 or E.14 or H.4.
. This could be a TKT E.6 or E.14 or H.4.
For the last two cases, Magma failed to determine the TKT. Nevertheless, none of the discriminants
![]()
is particularly spectacular.
Example 5.2.
We also checked all 122444 IPADs for complex quadratic fields with type ![]() in the range
in the range ![]() of discriminants, Again, we found exactly 5 errors among these IPADs which had been computed by PARI/GP [1] in [10] . For the recomputation we used MAGMA [4] . The study of this extensive material was very helpful for the deeper understanding of 3-groups having abelianization of type
of discriminants, Again, we found exactly 5 errors among these IPADs which had been computed by PARI/GP [1] in [10] . For the recomputation we used MAGMA [4] . The study of this extensive material was very helpful for the deeper understanding of 3-groups having abelianization of type![]() . Systematic results in the style of Theorems 3.1 and 3.2 will be given in a forthcoming paper. The abbreviation pTKT means the punctured TKT.
. Systematic results in the style of Theorems 3.1 and 3.2 will be given in a forthcoming paper. The abbreviation pTKT means the punctured TKT.
1) For![]() , the erroneous IPAD
, the erroneous IPAD ![]() contained
contained
the malformed component ![]() instead of the correct
instead of the correct![]() . This could be a homocyclic pTKT B.2 or C.4 or D.5.
. This could be a homocyclic pTKT B.2 or C.4 or D.5.
2) For d = −79749087, the erroneous IPAD ![]() contained the mal-
contained the mal-
formed component ![]() instead of the correct
instead of the correct![]() . It is a pTKT D.11,
. It is a pTKT D.11,![]() .
.
3) For![]() , the erroneous IPAD
, the erroneous IPAD ![]() contained
contained
the malformed component ![]() instead of the correct
instead of the correct![]() . It could be a homocyclic pTKT B.2 or C.4 or D.5.
. It could be a homocyclic pTKT B.2 or C.4 or D.5.
4) For![]() , the erroneous IPAD
, the erroneous IPAD ![]() contained the
contained the
malformed component ![]() instead of the correct
instead of the correct![]() . This could be a pTKT B.2 or C.4 or D.5 in the first excited state.
. This could be a pTKT B.2 or C.4 or D.5 in the first excited state.
5) For d = −86139199, the erroneous IPAD ![]() contained the mal-
contained the mal-
formed component ![]() instead of the correct
instead of the correct![]() . This is clearly a pTKT D.11,
. This is clearly a pTKT D.11,![]() .
.
Again, none of the corresponding discriminants
![]()
is particularly spectacular.
We emphasize that, in both Examples 5.1 and 5.2, the errors of PARI/GP [1] occured in the upper limit range of absolute discriminants above 70 millions. This seems to be a critical region of extreme computing where current computational algebra systems become unstable. MAGMA [4] also often fails to compute the TKT in that range.
Fortunately, there appeared a single discriminant only for each of the 5 erroneous IPADs, in both examples. This indicates that the errors are not systematic but rather stochastic.
5.2. Application 2: Completing Partial Capitulation Types
Example 5.3. For the discriminant ![]() of the complex quadratic field
of the complex quadratic field ![]() with 3-class
with 3-class
group of type![]() , we constructed the four unramified cyclic cubic extensions
, we constructed the four unramified cyclic cubic extensions![]() ,
, ![]() , and com-
, and com-
puted the IPAD ![]() with the aid of MAGMA [4] .
with the aid of MAGMA [4] .
According to Equation (20) in Theorem 3.2, the second 3-class group G of K must be of coclass![]() , and the polarized component 54 of the IPAD shows that
, and the polarized component 54 of the IPAD shows that ![]() and thus the nilpotency class
and thus the nilpotency class ![]() and the defect of commutativity
and the defect of commutativity ![]() are given by either
are given by either![]() ,
, ![]() , or
, or![]() ,
,![]() . Further, in view of the rank-3 component
. Further, in view of the rank-3 component ![]() of the IPAD,
of the IPAD, ![]() must be a vertex of the coclass tree
must be a vertex of the coclass tree![]() .
.
When we tried to determine the 3-principalization type![]() , Magma succeeded in calculating
, Magma succeeded in calculating ![]() and
and ![]() but unfortunately failed to give
but unfortunately failed to give ![]() and
and![]() . With respect to the complete IPAD, Theorem 4.1 enforces
. With respect to the complete IPAD, Theorem 4.1 enforces ![]() (item (1)) and
(item (1)) and ![]() (item (2)), and therefore the partial result
(item (2)), and therefore the partial result ![]() is completed to
is completed to![]() . According to item (3) of Remark 4.2 or item (3) of Corollary 4.1,
. According to item (3) of Remark 4.2 or item (3) of Corollary 4.1, ![]() is of TKT H.4. Our experience suggests that this TKT compels the arrangement
is of TKT H.4. Our experience suggests that this TKT compels the arrangement![]() ,
, ![]() , expressed by the weak leaf conjecture ( [9] , Cnj. 3.1, p. 423).
, expressed by the weak leaf conjecture ( [9] , Cnj. 3.1, p. 423).
Example 5.4. For the discriminant ![]() of the complex quadratic field
of the complex quadratic field ![]() with 3-class
with 3-class
group of type![]() , we constructed the four unramified cyclic cubic extensions
, we constructed the four unramified cyclic cubic extensions![]() ,
, ![]() , and com-
, and com-
puted the IPAD ![]() with the aid of MAGMA [4] .
with the aid of MAGMA [4] .
According to Equation (20) in Theorem 3.2, the second 3-class group ![]() of
of ![]() must be of coclass
must be of coclass![]() , and the polarized component 54 of the IPAD shows that
, and the polarized component 54 of the IPAD shows that ![]() and thus the nilpotency class
and thus the nilpotency class ![]() and the defect of commutativity
and the defect of commutativity ![]() are given by either
are given by either![]() ,
, ![]() , or
, or![]() ,
,![]() . Further, due to the lack of a rank-3 component
. Further, due to the lack of a rank-3 component ![]() in the IPAD,
in the IPAD, ![]() must be a vertex of the coclass tree
must be a vertex of the coclass tree![]() .
.
Next, we tried to determine the 3-principalization type![]() . Magma succeeded in calculating two fixed points
. Magma succeeded in calculating two fixed points ![]() and
and ![]() but unfortunately failed to give
but unfortunately failed to give ![]() and
and![]() . With respect to the complete IPAD, Theorem 4.2 enforces
. With respect to the complete IPAD, Theorem 4.2 enforces ![]() or
or ![]() (item (1)), and
(item (1)), and ![]() or
or ![]() (item (2)), and therefore the partial result
(item (2)), and therefore the partial result ![]() is completed to
is completed to ![]() or
or![]() . According to item (1) of Remark 4.4 or item (3) of Corollary 4.2,
. According to item (1) of Remark 4.4 or item (3) of Corollary 4.2, ![]() is of TKT E.8, and this TKT enforces the arrangement
is of TKT E.8, and this TKT enforces the arrangement![]() ,
, ![]() , since
, since ![]() is impossible.
is impossible.
Example 5.5. For the discriminant ![]() of the complex quadratic field
of the complex quadratic field ![]() with 3-
with 3-
class group of type![]() , we constructed the four unramified cyclic cubic extensions
, we constructed the four unramified cyclic cubic extensions![]() ,
, ![]() , and
, and
computed the IPAD ![]() with the aid of MAGMA [4] .
with the aid of MAGMA [4] .
According to Equation (20) in Theorem 3.2, the second 3-class group G of K must be of coclass![]() , and the polarized component 65 of the IPAD shows that
, and the polarized component 65 of the IPAD shows that ![]() and thus the nilpotency class
and thus the nilpotency class ![]() and the defect of commutativity
and the defect of commutativity ![]() are given by either
are given by either![]() ,
, ![]() , or
, or![]() ,
,![]() . Further, in view of the rank-3 component
. Further, in view of the rank-3 component ![]() of the IPAD,
of the IPAD, ![]() must be a vertex of the coclass tree
must be a vertex of the coclass tree![]() .
.
Then we tried to determine the 3-principalization type![]() . Magma succeeded in calculating
. Magma succeeded in calculating ![]() and
and ![]() but unfortunately failed to give
but unfortunately failed to give ![]() and
and![]() . With respect to the complete IPAD, Theorem 4.1 enforces
. With respect to the complete IPAD, Theorem 4.1 enforces ![]() and
and ![]() (item (2)), whereas the claim in item (1) is confirmed, and therefore the partial result
(item (2)), whereas the claim in item (1) is confirmed, and therefore the partial result ![]() is completed to
is completed to![]() . According to item (2) of Remark 4.2 or item (3) of Corollary 4.1,
. According to item (2) of Remark 4.2 or item (3) of Corollary 4.1, ![]() is of TKT E.14, and this TKT enforces the arrangement
is of TKT E.14, and this TKT enforces the arrangement![]() ,
, ![]() , since
, since ![]() is impossible.
is impossible.
6. Iterated IPADs of Second Order
In this section, where generally![]() , we apply iterated IPADs of second order for indirectly computing
, we apply iterated IPADs of second order for indirectly computing ![]() - capitulation types in Section 6.1 and finding the exact length of
- capitulation types in Section 6.1 and finding the exact length of ![]() -class towers in Section 6.2.
-class towers in Section 6.2.
6.1. p-Capitulation Type
By means of the following theorem, the exact 3-principalization type ![]() [9] [19] [21] of real quadratic fields
[9] [19] [21] of real quadratic fields
![]() ,
, ![]() , can be determined indirectly with the aid of information on the structure of 3-class groups
, can be determined indirectly with the aid of information on the structure of 3-class groups
of number fields of absolute degree![]() .
.
Theorem 6.1. (Indirect computation of the ![]() -capitulation type)
-capitulation type)
Suppose that ![]() and let
and let ![]() be a number field with 3-class group
be a number field with 3-class group ![]() of type
of type ![]() and 3-tower group
and 3-tower group![]() .
.
1) If the IPAD of ![]() is given by
is given by
![]()
then by Equation (14) in Theorem 3.1,
![]()
in particular, the length of the 3-class tower of ![]() is given by
is given by![]() .
.
2) If the first layer ![]() of abelian unramified extensions of
of abelian unramified extensions of ![]() consists of
consists of![]() , then the iterated IPAD of second order
, then the iterated IPAD of second order
![]()
admits a sharp decision about the group ![]() and the first layer of the transfer kernel type
and the first layer of the transfer kernel type
![]()
![]() (25)
(25)
if and only if![]() , and thus
, and thus![]() .
.
![]() (26)
(26)
if and only if![]() , and thus
, and thus![]() .
.
![]() (27)
(27)
if and only if![]() , and thus
, and thus![]() .
.
Proof. It suffices to compute the iterated IPADs of the groups ![]() with the aid of MAGMA [4] , simply by investigating their four maximal normal subgroups
with the aid of MAGMA [4] , simply by investigating their four maximal normal subgroups![]() ,
,![]() . □
. □
Example 6.1. A possible future application of Theorem 6.1 could be, for instance, the separation of the capitulation types a.2, ![]() , and a.3,
, and a.3, ![]() , among the 1386 real quadratic fields
, among the 1386 real quadratic fields
![]() ,
, ![]() , with 3-class group
, with 3-class group ![]() of type
of type ![]() and IPAD
and IPAD![]() ,
,
which was outside of our reach in all investigations of ( [23] , Tbl. 2, p. 496), ( [5] , Tbl. 6.1, p. 451) and ( [9] , Figure 3.2, p. 422). The reason why we expect this enterprise to be promising is that our experience with MAGMA [4] shows that computing class groups can become slow but remains sound and stable for huge discriminants![]() , whereas the calculation of capitulation kernels frequently fails.
, whereas the calculation of capitulation kernels frequently fails.
6.2. Length of the p-Class Tower
In this section, we use the iterated IPAD of second order ![]() for the
for the
indirect computation of the length ![]() of the
of the ![]() -class tower of a number field
-class tower of a number field ![]() with
with ![]() -tower group
-tower group![]() , where
, where ![]() denotes a fixed prime.
denotes a fixed prime.
We begin with theorems which permit a decision between finitely many possibilities for the length ![]() in Section 6.2.1. These results systematically extend the investigations of complex quadratic fields in [6] to arbitrary base fields
in Section 6.2.1. These results systematically extend the investigations of complex quadratic fields in [6] to arbitrary base fields ![]() and yield the first examples of real quadratic fields having a
and yield the first examples of real quadratic fields having a ![]() -class tower of exact length three. Then, in Section 6.2.3, we launch the first successful attack against quadratic fields
-class tower of exact length three. Then, in Section 6.2.3, we launch the first successful attack against quadratic fields ![]() whose second
whose second ![]() -class group
-class group ![]() possesses an infinite cover ( [16] , Dfn.21.2), and for which the problem of finding the length
possesses an infinite cover ( [16] , Dfn.21.2), and for which the problem of finding the length ![]() was completely unsolved up to now [13] . In Section 6.2.2, some prerequisites con- cerning periodic bifurcations are provided.
was completely unsolved up to now [13] . In Section 6.2.2, some prerequisites con- cerning periodic bifurcations are provided.
6.2.1. Second p-Class Groups with Finite Cover
In the following theorems, we must use extended identifiers [4] [24] [25] of finite 3-groups with order bigger than![]() , which lie outside of the SmallGroups database [17] [18] . This was explained in ( [16] , Section 9).
, which lie outside of the SmallGroups database [17] [18] . This was explained in ( [16] , Section 9).
Theorem 6.2. (Length ![]() of the 3-class tower for
of the 3-class tower for![]() )
)
Suppose that ![]() and let
and let ![]() be a number field with 3-class group
be a number field with 3-class group ![]() of type
of type ![]() and 3-tower group
and 3-tower group![]() .
.
1) If the IPAD of ![]() is given by
is given by
![]()
and the first layer TKT ![]() neither contains a total principalization nor a 2-cycle, then there are two possi- bilities
neither contains a total principalization nor a 2-cycle, then there are two possi- bilities ![]() for the length of the 3-class tower of
for the length of the 3-class tower of![]() .
.
2) If the first layer ![]() of abelian unramified extensions of
of abelian unramified extensions of ![]() consists of
consists of![]() , then the iterated IPAD of second order
, then the iterated IPAD of second order
![]()
admits a sharp decision about the length![]() .
.
![]() (28)
(28)
if and only if![]() , and thus
, and thus![]() .
.
![]() (29)
(29)
if and only if![]() , and thus
, and thus![]() .
.
Proof. According to Theorem 3.2, an IPAD of the form ![]() indicates that the
indicates that the
metabelianization of the group ![]() belongs to the coclass tree
belongs to the coclass tree ![]() ( [9] , Figure 3.6, p. 442) and has nilpotency class
( [9] , Figure 3.6, p. 442) and has nilpotency class![]() , due to the polarization.
, due to the polarization.
According to Section 4.1, the lack of a total principalization excludes the TKT c.18 and the absence of a 2-cycle discourages the TKT H.4, whence the group ![]() must be of TKT E.6 or E.14.
must be of TKT E.6 or E.14.
By means of the techniques described in ( [6] , Proof of Thm. 4.1), a search in the complete descendant tree![]() , not restricted to groups of coclass 2, yields exactly six candidates for the group G: three metabe- lian groups
, not restricted to groups of coclass 2, yields exactly six candidates for the group G: three metabe- lian groups ![]() with
with![]() , and three groups of derived length 3 and order
, and three groups of derived length 3 and order ![]() with gene- ralized identifiers
with gene- ralized identifiers ![]()
![]() . There cannot exist adequate groups of bigger orders ( [6] , Cor. 3.0.1). The former three groups are charcterized by Equations (28) the latter three groups (see [16] , 21.2, Figure 8) by Equations (29).
. There cannot exist adequate groups of bigger orders ( [6] , Cor. 3.0.1). The former three groups are charcterized by Equations (28) the latter three groups (see [16] , 21.2, Figure 8) by Equations (29).
Finally, we have![]() . □
. □
Theorem 6.3. (Length ![]() of the 3-class tower for
of the 3-class tower for![]() )
)
Suppose that ![]() and let
and let ![]() be a number field with 3-class group
be a number field with 3-class group ![]() of type
of type ![]() and 3-tower group
and 3-tower group![]() .
.
1) If the IPAD of ![]() is given by
is given by
![]()
and the first layer TKT ![]() neither contains a total principalization nor a 2-cycle, then there are two possi- bilities
neither contains a total principalization nor a 2-cycle, then there are two possi- bilities ![]() for the length of the 3-class tower of
for the length of the 3-class tower of![]() .
.
2) If the first layer ![]() of abelian unramified extensions of
of abelian unramified extensions of ![]() consists of
consists of![]() , then the iterated IPAD of second order
, then the iterated IPAD of second order
![]()
admits a sharp decision about the length![]() .
.
![]() (30)
(30)
if and only if![]() , and thus
, and thus![]() .
.
![]() (31)
(31)
if and only if![]() , and thus
, and thus![]() .
.
Proof. According to Theorem 3.2, an IPAD of the form ![]() indicates that the metabe-
indicates that the metabe-
lianization of the group ![]() belongs to the coclass tree
belongs to the coclass tree ![]() ( [9] , Figure 3.7, p. 443) and has nil- potency class
( [9] , Figure 3.7, p. 443) and has nil- potency class![]() , due to the polarization.
, due to the polarization.
According to Section 4.2, the lack of a total principalization excludes the TKT c.21 and the absence of a 2-cycle discourages the TKT G.16, whence the group ![]() must be of TKT E.8 or E.9.
must be of TKT E.8 or E.9.
As we have shown in detail in [6] , Proof of Thm. 4.1], a search in the complete descendant tree![]() , not restricted to groups of coclass 2, yields exactly six candidates for the group
, not restricted to groups of coclass 2, yields exactly six candidates for the group![]() : three metabelian groups
: three metabelian groups ![]() with
with![]() , and three groups of derived length 3 and order
, and three groups of derived length 3 and order ![]() with generalized identifiers
with generalized identifiers ![]()
![]() . There cannot exist adequate groups of bigger orders ([6] , Cor. 3.0.1). The former three groups are characterized by Equations (30) the latter three groups (see [16] , Section 21.2, Figure 9) by Equations (31).
. There cannot exist adequate groups of bigger orders ([6] , Cor. 3.0.1). The former three groups are characterized by Equations (30) the latter three groups (see [16] , Section 21.2, Figure 9) by Equations (31).
Eventually, the 3-tower length of![]() ,
, ![]() , coincides with the derived length of
, coincides with the derived length of![]() . □
. □
Example 6.2. (The first real quadratic field ![]() with
with![]() .) In June 2006, we discovered the smallest
.) In June 2006, we discovered the smallest
discriminant ![]() of a real quadratic field
of a real quadratic field ![]() with 3-class group of type
with 3-class group of type ![]() whose
whose
3-tower group ![]() possesses the transfer kernel type E.9,
possesses the transfer kernel type E.9, ![]() ([19] , Tbl. 4, p. 498).
([19] , Tbl. 4, p. 498).
The complex quadratic analogue ![]() was known since 1934 by the famous paper of Scholz and
was known since 1934 by the famous paper of Scholz and
Taussky [20] . However, it required almost 80 years until M.R. Bush and ourselves ([6] , Cor. 4.1.1) succeeded in providing the first faultless proof that ![]() has a 3-class tower of exact length
has a 3-class tower of exact length ![]() with
with ![]() -tower group
-tower group ![]() isomorphic to one of the two Schur
isomorphic to one of the two Schur ![]() -groups
-groups ![]()
![]() of order
of order![]() .
.
For![]() , the methods in [6] do not admit a final decision about the length
, the methods in [6] do not admit a final decision about the length![]() . They only
. They only
yield four possible 3-tower groups of K, namely either the two unbalanced groups ![]() with
with ![]() and relation rank
and relation rank ![]() bigger than the generator rank
bigger than the generator rank ![]() or the two Schur
or the two Schur ![]() -groups
-groups ![]() with
with ![]() and
and ![]() equal to
equal to![]() .
.
In October 2014, we succeeded in proving that three of the unramified cyclic cubic extensions ![]() reveal
reveal
the critical IPAD component ![]() in Equation (31) of Theorem 6.3, item (2), whence also
in Equation (31) of Theorem 6.3, item (2), whence also
![]() and
and![]() . This was done by computing 3-class groups of number fields of ab- solute degree 6 × 3 = 18 with the aid of MAGMA [4] .
. This was done by computing 3-class groups of number fields of ab- solute degree 6 × 3 = 18 with the aid of MAGMA [4] .
6.2.2. Another Descendant Tree with Periodic Bifurcations
In ( [16] , Section 21.2), we provided computational evidence of periodic bifurcations in pruned descendant trees with roots![]() . Now we want to show that the immediate descendant
. Now we want to show that the immediate descendant ![]() of another root
of another root ![]() possesses an infinite balanced cover ( [16] , Dfn. 21.2). For this purpose we construct an extensive finite part of the descendant tree
possesses an infinite balanced cover ( [16] , Dfn. 21.2). For this purpose we construct an extensive finite part of the descendant tree ![]() with the aid of MAGMA [4] and we combine the gained insight with results of L. Bartholdi and M.R. Bush [13] . The group
with the aid of MAGMA [4] and we combine the gained insight with results of L. Bartholdi and M.R. Bush [13] . The group ![]() has been called the non-CF group
has been called the non-CF group ![]() by J. Ascione, G. Havas and C.R. Leedham-Green [26] [27] .
by J. Ascione, G. Havas and C.R. Leedham-Green [26] [27] .
For brevity, we give 3-logarithms of abelian type invariants in the following theorem and we denote iteration
by formal exponents, for instance, ![]() ,
, ![]() ,
, ![]() , and we eliminate
, and we eliminate
initial anomalies of generalized identifiers by putting
![]() , for
, for![]() , formally. (Observe that actually
, formally. (Observe that actually
![]() , whereas
, whereas![]() .)
.)
Theorem 6.4. Let ![]() be a positive integer bounded from above by 8.
be a positive integer bounded from above by 8.
1) In the descendant tree ![]() of
of![]() , there exists a unique path with length
, there exists a unique path with length ![]() of
of ![]() -groups ( [16] , Dfn. 10.1),
-groups ( [16] , Dfn. 10.1),
![]()
and (reverse) directed edges with alternating step sizes 1 and 2 such that![]() , for all
, for all ![]() (
(![]() is a section of the surjection
is a section of the surjection ![]() on this path), and all the vertices with even superscript i = 2j,
on this path), and all the vertices with even superscript i = 2j, ![]() ,
,
![]() (32)
(32)
resp. all the vertices with odd superscript ![]()
![]() ,
,
![]() (33)
(33)
of this path share the following common invariants, respectively:
-the uniform IPAD
![]() (34)
(34)
-the uniform transfer kernel type
![]() (35)
(35)
-the 3-multiplicator rank and the nuclear rank [14] [16] ,
![]() (36)
(36)
resp., giving rise to the bifurcations for odd![]() ,
,
![]() (37)
(37)
-and the counters of immediate descendants [16] [18] ,
![]() (38)
(38)
resp.
![]() (39)
(39)
determining the local structure of the descendant tree.
2) A few other invariants of the vertices ![]() depend on the superscript
depend on the superscript![]() ,
,
-the 3-logarithm of the order, the nilpotency class and the coclass,
![]() (40)
(40)
resp.
![]() (41)
(41)
Theorem 6.4 provides the scaffold of the pruned descendant tree ![]() of
of ![]() with the dis- tinguished path and periodic bifurcations.
with the dis- tinguished path and periodic bifurcations.
With respect to our intended applications, however, the following Corollaries 6.1 and 6.2 are of the greatest importance.
Corollary 6.1. Let ![]() be a non-negative integer, where
be a non-negative integer, where![]() .
.
Whereas the vertices with even superscript![]() ,
, ![]() , that is,
, that is, ![]() , are merely links in the distinguished path, the vertices with odd superscript
, are merely links in the distinguished path, the vertices with odd superscript ![]()
![]() , that is,
, that is,
![]() , reveal the essential periodic bifurcations with the following properties.
, reveal the essential periodic bifurcations with the following properties.
1) The regular component ![]() of the descendant tree
of the descendant tree ![]() is a finite tree which contains the root and four terminal
is a finite tree which contains the root and four terminal ![]() -groups,
-groups,
![]()
2) The irregular component ![]() of the descendant tree
of the descendant tree ![]() is a forest which con- tains a single isolated Schur
is a forest which con- tains a single isolated Schur ![]() -group
-group
![]()
and additionally contains the next vertex of the distinguished path![]() .
.
Remark 6.1. We apply a sifting strategy for reducing the entire descendant tree ![]() to a pruned des- cendant tree
to a pruned des- cendant tree ![]() by filtering all vertices which are
by filtering all vertices which are ![]() -groups. The process consists of
-groups. The process consists of
1) keeping the unique terminal step size-2 descendant, which is exactly the Schur ![]() -group
-group![]() , the unique capable step size-2 descendant, and the 4 terminal step size-1 descendants
, the unique capable step size-2 descendant, and the 4 terminal step size-1 descendants![]() ,
, ![]() , which are
, which are ![]() - groups, of
- groups, of![]() ,
, ![]() , and
, and
2) eliminating ([16] , Section 20, (F1)) the 3 non-![]() groups, together with their complete descendant trees, among the 4capable step size-1 descendants of
groups, together with their complete descendant trees, among the 4capable step size-1 descendants of![]() ,
,![]() .
.
A finite part at the top of the resulting tree ![]() is drawn in Figure 1.
is drawn in Figure 1.
Proof. (of Theorem 6.4, and Corollary 6.1)
The ![]() -group generation algorithm [28] [29] , which is implemented in the computational algebra system MAGMA [2] - [4] , was used for constructing the pruned descendant tree
-group generation algorithm [28] [29] , which is implemented in the computational algebra system MAGMA [2] - [4] , was used for constructing the pruned descendant tree ![]() with root
with root ![]() which was defined as the disjoint union of all regular components, i.e. finite trees
which was defined as the disjoint union of all regular components, i.e. finite trees
![]()
with the descendants![]() ,
, ![]() , of
, of ![]() as roots, together with 2siblings in the irregular component
as roots, together with 2siblings in the irregular component
![]()
one of them the Schur ![]() -group
-group ![]() with 3-multiplicator rank
with 3-multiplicator rank ![]() and nuclear rank
and nuclear rank![]() , the other
, the other ![]() the next vertex of the distinguished path.
the next vertex of the distinguished path.
The vertical construction was terminated for ![]() at nilpotency class 2 × 8 + 3 = 19. The horizontal construction was extended up to coclass
at nilpotency class 2 × 8 + 3 = 19. The horizontal construction was extended up to coclass![]() , where the consumption of CPU time became annoying. □
, where the consumption of CPU time became annoying. □
The extent to which we constructed the pruned descendant tree ![]() suggests the following con- jecture.
suggests the following con- jecture.
Conjecture 6.1. Theorem 6.4 and Corollary 6.1 remain true for an arbitrarily large positive integer![]() , not necessarily bounded by 8.
, not necessarily bounded by 8.
For the convenience of the reader, we now recall ( [16] , Dfn. 21.2):
Definition 6.1. Let ![]() be a finite metabelian
be a finite metabelian ![]() -group, then the set of all finite non-metabelian
-group, then the set of all finite non-metabelian ![]() -groups
-groups ![]() whose second derived quotient
whose second derived quotient ![]() is isomorphic to
is isomorphic to ![]() is called the cover
is called the cover ![]() of
of![]() . The subset
. The subset ![]() consisting of Schur
consisting of Schur ![]() -groups in
-groups in ![]() is called the balanced cover of
is called the balanced cover of![]() .
.
Corollary 6.2. The group![]() , which does not have a balanced presentation, has an infinite cover and even an infinite balanced cover. More precisely, the covers are given explicitly by
, which does not have a balanced presentation, has an infinite cover and even an infinite balanced cover. More precisely, the covers are given explicitly by
![]() (42)
(42)
For the proof, we have to recall that L. Bartholdi and M.R. Bush ( [13] , Thm. 2.1, p. 160, and Prop. 3.6, p. 165) have constructed an infinite family ![]() of Schur
of Schur ![]() -groups with strictly increasing 3-power order, nil- potency class, coclass, and increasing unbounded derived length
-groups with strictly increasing 3-power order, nil- potency class, coclass, and increasing unbounded derived length
![]()
Figure 1. Periodic bifurcations in the pruned descendant tree![]() .
.
![]() (43)
(43)
such that ![]() is the well-known metabelian two-stage tower group
is the well-known metabelian two-stage tower group ![]() of the complex qua-
of the complex qua-
dratic field ![]() ( [9] , Thm. 1.5, p. 407), ( [20] , pp. 22-25), ( [30] , p. 20) with IPAD
( [9] , Thm. 1.5, p. 407), ( [20] , pp. 22-25), ( [30] , p. 20) with IPAD
![]() . All the other members
. All the other members ![]() of the family with
of the family with ![]() are non-metabelian and share
are non-metabelian and share
the common IPAD![]() .
.
Proof. Several issues must be clarified for the groups ![]() with
with![]() .
.
Firstly, according to the Equations (15) and (16) in Theorem 3.1, there are only five possibilities for the metabelianizations![]() , namely the groups
, namely the groups ![]() and
and![]() . However, we can eliminate
. However, we can eliminate![]() , because it has an empty cover by ( [9] , Thm. 1.4, p. 406). We can also cancel
, because it has an empty cover by ( [9] , Thm. 1.4, p. 406). We can also cancel ![]() by ([6] , Lem. 3.3), since they fail to be
by ([6] , Lem. 3.3), since they fail to be ![]() -groups. In fact, the same arguments as for the
-groups. In fact, the same arguments as for the ![]()
![]() apply to all vertices of the pruned tree
apply to all vertices of the pruned tree![]() , since they are
, since they are ![]() -groups, by definition. This shows that
-groups, by definition. This shows that
![]() (44)
(44)
Secondly, we have to make sure that the ![]()
![]() , and more generally all finite 3-groups
, and more generally all finite 3-groups ![]() with IPAD
with IPAD
![]() , are descendants of
, are descendants of![]() . Since the abelian 3-group with type invariants 21 is not a quotient
. Since the abelian 3-group with type invariants 21 is not a quotient
of![]() , ([6] , Cor. 3.0.1) shows that such a group
, ([6] , Cor. 3.0.1) shows that such a group ![]() cannot be descendant of any other sibling
cannot be descendant of any other sibling ![]() with
with ![]() of
of![]() , which contains at least two maximal subgroups of type 21. According to Equation (14) in Theorem 3.1, the unique remaining possibility for an ancestor having the required IPAD
, which contains at least two maximal subgroups of type 21. According to Equation (14) in Theorem 3.1, the unique remaining possibility for an ancestor having the required IPAD
![]() is the extra special group
is the extra special group![]() . However, this group has been exhausted completely already,
. However, this group has been exhausted completely already,
since it gives rise to exactly the seven immediate step size-2 descendants ![]() with
with![]() , mentioned above.
, mentioned above.
Finally, the Schur ![]() -groups Gn
-groups Gn ![]() must necessarily coincide with the periodic sequence
must necessarily coincide with the periodic sequence ![]()
![]() of Schur
of Schur ![]() -groups, whose initial sections were constructed in Corollary 6.1, and which must be continued in- ductively in the sense of Conjecture 6.1:
-groups, whose initial sections were constructed in Corollary 6.1, and which must be continued in- ductively in the sense of Conjecture 6.1:
![]() (45)
(45)
Indeed, since each ![]() is a sibling of
is a sibling of![]() , for
, for![]() , having identical invariants, Equation (40) in Theorem 6.4 shows that all invariants of
, having identical invariants, Equation (40) in Theorem 6.4 shows that all invariants of ![]() coincide with those of
coincide with those of ![]()
![]() (46)
(46)
Consequently, the inclusions in Equation (44) can be replaced by equalities, and the claims of Corollary 6.2 are proved. □
Remark 6.2.
1) The claims of Conjecture 6.1 are strongly supported by the proven infinitude of the family ![]() of Schur
of Schur ![]() -groups in [13] and their obvious coincidence with the periodic sequence
-groups in [13] and their obvious coincidence with the periodic sequence ![]() in Corollary 6.1.
in Corollary 6.1.
2) The IPAD ![]() is a considerably more restrictive condition for a pro-3 group than the TKT
is a considerably more restrictive condition for a pro-3 group than the TKT
H.4, ![]() , which is necessarily the TKT of all descendants of
, which is necessarily the TKT of all descendants of ![]() , by ( [6] , Cor.3.0.2). However, the TKT H.4 is unable to characterize the vertices of the tree of
, by ( [6] , Cor.3.0.2). However, the TKT H.4 is unable to characterize the vertices of the tree of ![]() uniquely, since there are lots of vertices with TKT H.4 in the tree of
uniquely, since there are lots of vertices with TKT H.4 in the tree of ![]() , and, as we have seen in Remark 4.2, the same is true for the tree of
, and, as we have seen in Remark 4.2, the same is true for the tree of ![]() , since
, since ![]() and
and ![]() are equivalent ( [21] , Section 3, p. 79).
are equivalent ( [21] , Section 3, p. 79).
3) The exact specification of the infinite cover, resp. the infinite and entirely non-metabelian balanced cover, of ![]() in Corollary 6.2 implies that the length
in Corollary 6.2 implies that the length ![]() of the 3-class tower of a real, resp. complex,
of the 3-class tower of a real, resp. complex,
quadratic field ![]() with IPAD
with IPAD ![]() can take any value bigger than 1, resp. 2, or even
can take any value bigger than 1, resp. 2, or even
![]() . In the complex case, the 3-tower group must be a Schur
. In the complex case, the 3-tower group must be a Schur ![]() -group, according to [6] [10] [31] [32] .
-group, according to [6] [10] [31] [32] .
6.2.3. Second p-Class Groups with Infinite Cover
As a final coronation of this section, we show that our new IPAD strategies are powerful enough to enable the
determination of the length ![]() for some quadratic fields
for some quadratic fields ![]() with IPAD
with IPAD
![]() with the aid of information on the structure of 3-class groups of number fields of ab-
with the aid of information on the structure of 3-class groups of number fields of ab-
solute degree![]() . This is close to the limits of what can currently be done with MAGMA [4] on powerful machines.
. This is close to the limits of what can currently be done with MAGMA [4] on powerful machines.
For this purpose, we extend the concept of iterated IPADs of second order
![]()
once more by adding the second layers ![]() to all IPADs
to all IPADs ![]() of unramified degree-
of unramified degree-![]() extensions
extensions![]() . The resulting iterated multi-layered IPAD of second order is indicated by an asterisk
. The resulting iterated multi-layered IPAD of second order is indicated by an asterisk
![]()
Theorem 6.5. (Length ![]() of the 3-class tower for
of the 3-class tower for![]() )
)
Suppose that ![]() and let
and let ![]() be a quadratic number field with 3-class group
be a quadratic number field with 3-class group ![]() of type
of type ![]() and 3-tower group
and 3-tower group![]() .
.
1) If the IPAD of ![]() is given by
is given by
![]()
then the first layer TKT is ![]() and there exist infinitely many possibilities
and there exist infinitely many possibilities ![]() for the length of the 3-class tower of
for the length of the 3-class tower of![]() .
.
2) If the first layer ![]() of abelian unramified extensions of
of abelian unramified extensions of ![]() consists of
consists of![]() , then the iterated multi-layered IPAD of second order
, then the iterated multi-layered IPAD of second order
![]()
admits certain partial decisions about the length ![]() as follows.
as follows.
![]() (47)
(47)
if and only if![]() , and thus
, and thus![]() .
.
![]() (48)
(48)
if and only if![]() , and thus
, and thus![]() .
.
![]() (49)
(49)
if and only if![]() , and thus
, and thus![]() .
.
![]() (50)
(50)
if and only if either ![]() or
or![]() , and thus
, and thus![]() .
.
![]() (51)
(51)
if and only if![]() , and thus
, and thus![]() .
.
![]() (52)
(52)
if and only if either ![]() or
or![]() , both of order 38, and thus
, both of order 38, and thus![]() .
.
![]() (53)
(53)
occurs for ![]() of order
of order![]() , where
, where![]() .
.
![]() (54)
(54)
occurs for either ![]()
or ![]()
or![]() , all of order
, all of order![]() , where
, where![]() .
.
![]() (55)
(55)
occurs for ![]() of order
of order![]() , where
, where![]() .
.
![]() (56)
(56)
occurs for either
![]() ,
, ![]() , of order
, of order![]() , where
, where![]() ,
,
or ![]() of order
of order![]() , where
, where![]() .
.
The various groups which occur in Theorem 6.5 are drawn in the tree diagram of Figure 1. This diagram im- pressively visualizes periodically repeating bifurcations in the descendant tree ![]() of Ascione’s non-CF group
of Ascione’s non-CF group![]() . An essential difference to the trees
. An essential difference to the trees ![]() and
and ![]() in ([16] , Section 21.2), where
in ([16] , Section 21.2), where ![]() and
and![]() , is that the regular component
, is that the regular component ![]() of each vertex
of each vertex ![]() with coclass
with coclass ![]() and nuclear rank
and nuclear rank![]() , giving rise to a bifurcation, is not a coclass tree but rather a finite tree with root and four terminal immediate descendants. The irregular component
, giving rise to a bifurcation, is not a coclass tree but rather a finite tree with root and four terminal immediate descendants. The irregular component ![]() is a forest containing an isolated Schur
is a forest containing an isolated Schur ![]() -group and the parent of the next vertex with bifurcation (together with its regular com- ponent).
-group and the parent of the next vertex with bifurcation (together with its regular com- ponent).
Proof. If we restricted the statements to complex quadratic fields it would be sufficient to consider the Schur ![]() -groups
-groups![]() ,
, ![]() , in the descendant tree
, in the descendant tree![]() . But since we are also interested in the behaviour of real quadratic fields, we must determine the iterated multi-layered IPADs
. But since we are also interested in the behaviour of real quadratic fields, we must determine the iterated multi-layered IPADs ![]() of second order of all vertices
of second order of all vertices ![]() in the pruned descendant tree consisting of
in the pruned descendant tree consisting of ![]() -groups. We do this for the groups up to the order 317, which were constructed in Section 6.2.2, by investigating their four maximal normal subgroups
-groups. We do this for the groups up to the order 317, which were constructed in Section 6.2.2, by investigating their four maximal normal subgroups![]() ,
, ![]() , with the aid of MAGMA [4] . Finally, we make use of the relation
, with the aid of MAGMA [4] . Finally, we make use of the relation![]() . □
. □
We point out that Equation (56) cannot be used for a conclusive identification.
Example 6.3. (The first quadratic fields with TKT H.4 and![]() ) In December 2009, we discovered
) In December 2009, we discovered
the smallest discriminant ![]() of a real quadratic field
of a real quadratic field ![]() with 3-class group of type
with 3-class group of type
![]() whose 3-tower group
whose 3-tower group ![]() possesses the transfer kernel type H.4,
possesses the transfer kernel type H.4, ![]() ([19] , Tbl. 4, p. 498). In January 2010, we found two further examples
([19] , Tbl. 4, p. 498). In January 2010, we found two further examples![]() .
.
The complex quadratic analogue ![]() was known since 1982 by the paper of Heider and Schmithals ( [30] , p. 20), whereas Scholz and Taussky gave an erroneous TKT F.7,
was known since 1982 by the paper of Heider and Schmithals ( [30] , p. 20), whereas Scholz and Taussky gave an erroneous TKT F.7, ![]() ( [20] , Footnote, p. 36). There is another example
( [20] , Footnote, p. 36). There is another example ![]() in ( [30] , Tbl. 3, p. 19) and in November 1989, we found
in ( [30] , Tbl. 3, p. 19) and in November 1989, we found ![]()
([21] , p. 84). All these fields share the same IPAD![]() .
.
In February 2015, we succeeded in proving that the unramified cyclic cubic extensions![]() , for
, for ![]() , resp.
, resp.![]() , resp.
, resp.![]() , reveal the critical first and second layer IPAD components in Equation (52), resp. (56), resp. (51), of Theorem 6.5, item (2), whence cer- tainly
, reveal the critical first and second layer IPAD components in Equation (52), resp. (56), resp. (51), of Theorem 6.5, item (2), whence cer- tainly![]() , for all these fields, with the single exception of
, for all these fields, with the single exception of![]() , where also
, where also ![]() could be possible.
could be possible.
However, the 3-class tower groups ![]() of
of ![]() are different: for
are different: for ![]() we have the Schur
we have the Schur ![]() -group
-group ![]() of order
of order![]() , and for
, and for ![]() we have the unbalanced group
we have the unbalanced group![]() , which is distinguished by possessing three pairwise non-isomorphic maximal sub- groups of type
, which is distinguished by possessing three pairwise non-isomorphic maximal sub- groups of type![]() . For
. For![]() , the group remains unknown.
, the group remains unknown.
The justifications were conducted by computing 3-class groups of number fields of absolute degree 6 × 9 = 54 with the aid of MAGMA [4] on a machine with two XEON 8-core CPUs and 256 GB RAM.
7. Complex Quadratic Fields of 3-Rank Three
In this concluding section we present another intriguing application of IPADs.
Due to Koch and Venkov [32] , it is known that a complex quadratic field ![]() with 3-class rank
with 3-class rank ![]() has an infinite 3-class field tower
has an infinite 3-class field tower ![]() of length
of length![]() . In the time between 1973 and 1978, Diaz y Diaz [33] [34] and Buell [35] have determined the smallest absolute discri- minants
. In the time between 1973 and 1978, Diaz y Diaz [33] [34] and Buell [35] have determined the smallest absolute discri- minants ![]() of such fields. Recently, we have launched a computational project which aims at verifying these classical results and adding sophisticated arithmetical details. Below the bound
of such fields. Recently, we have launched a computational project which aims at verifying these classical results and adding sophisticated arithmetical details. Below the bound ![]() there exist 25 discri- minants
there exist 25 discri- minants ![]() of this kind, and 14 of the corresponding fields
of this kind, and 14 of the corresponding fields ![]() have a 3-class group
have a 3-class group ![]() of elementary abelian type
of elementary abelian type![]() . For each of these 14 fields, we determine the type of 3-principalization
. For each of these 14 fields, we determine the type of 3-principalization ![]() in the thirteen unramified cyclic cubic extensions
in the thirteen unramified cyclic cubic extensions ![]() of
of![]() , and the structure of the 3-class groups
, and the structure of the 3-class groups ![]() of these extensions, i.e., the IPAD of K. We characterize the metabelian Galois group
of these extensions, i.e., the IPAD of K. We characterize the metabelian Galois group ![]() of the second Hilbert 3-class field
of the second Hilbert 3-class field ![]() by means of kernels and targets of its Artin transfer homomorphisms [8] to maximal subgroups. We provide evidence of a wealth of structure in the set of infinite topological 3-class field tower groups
by means of kernels and targets of its Artin transfer homomorphisms [8] to maximal subgroups. We provide evidence of a wealth of structure in the set of infinite topological 3-class field tower groups ![]() by showing that the 14 groups
by showing that the 14 groups ![]() are pairwise non-isomorphic.
are pairwise non-isomorphic.
We summarize our results and their obvious conclusion in the following theorem.
Theorem 7.1.
There exist exactly 14 complex quadratic number fields ![]() with 3-class groups
with 3-class groups ![]() of type
of type ![]() and discriminants in the range
and discriminants in the range![]() . They have pairwise non-isomorphic
. They have pairwise non-isomorphic
1) second and higher 3-class groups![]() ,
, ![]() ,
,
2) infinite topological 3-class field tower groups![]() .
.
Before we come to the proof of Theorem 7.1 in Section 7.3, we collect basic numerical data concerning fields with ![]() in Section 7.1, and we completely determine sophisticated arithmetical invariants in Section 7.2 for all fields with
in Section 7.1, and we completely determine sophisticated arithmetical invariants in Section 7.2 for all fields with ![]() of type
of type![]() . The first attempt to do so for the smallest absolute discri- minant
. The first attempt to do so for the smallest absolute discri- minant ![]() with
with ![]() is due to Heider and Schmithals in ( [30] , Section 4, Tbl. 2, p. 18), but it resulted in partial success only.
is due to Heider and Schmithals in ( [30] , Section 4, Tbl. 2, p. 18), but it resulted in partial success only.
7.1. Discriminants ![]() of Fields
of Fields ![]() with Rank
with Rank ![]()
Since one of our aims is to investigate tendencies for the coclass of second and higher ![]() -class groups
-class groups
![]() ,
, ![]() , [9] [23] of a series of algebraic number fields
, [9] [23] of a series of algebraic number fields ![]() with infinite
with infinite ![]() -class
-class
field tower, for an odd prime![]() , the most obvious choice which suggests itself is to take the smallest
, the most obvious choice which suggests itself is to take the smallest
possible prime ![]() and to select complex quadratic fields
and to select complex quadratic fields![]() ,
, ![]() , having the simplest possi-
, having the simplest possi-
ble 3-class group ![]() of rank 3, that is, of elementary abelian type
of rank 3, that is, of elementary abelian type![]() .
.
The reason is that Koch and Venkov [32] have improved the lower bound of Golod, Shafarevich [31] [36] and Vinberg [37] for the ![]() -class rank
-class rank![]() , which ensures an infinite
, which ensures an infinite ![]() -class tower of a complex quadratic field
-class tower of a complex quadratic field![]() , from 4 to 3.
, from 4 to 3.
However, quadratic fields with 3-rank ![]() are sparse. Diaz y Diaz and Buell [33] - [35] [38] have determined the minimal absolute discriminant of such fields to be
are sparse. Diaz y Diaz and Buell [33] - [35] [38] have determined the minimal absolute discriminant of such fields to be![]() .
.
To provide an independent verification, we used the computational algebra system MAGMA [2] - [4] for compiling a list of all quadratic fundamental discriminants ![]() of fields
of fields ![]() with 3-class rank
with 3-class rank![]() . In 16 hours of CPU time we obtained the 25 desired discriminants and the abelian type in- variants (here written in 3-power form) of the corresponding 3-class groups
. In 16 hours of CPU time we obtained the 25 desired discriminants and the abelian type in- variants (here written in 3-power form) of the corresponding 3-class groups![]() , and also of the complete class groups
, and also of the complete class groups![]() , as given in Table 1. There appeared only one discriminant
, as given in Table 1. There appeared only one discriminant ![]() (No. 16) which is not contained in ( [34] , Appendix 1, p.68) already.
(No. 16) which is not contained in ( [34] , Appendix 1, p.68) already.
There are 14 discriminants, starting with![]() , such that
, such that ![]() is elementary abelian of type
is elementary abelian of type
![]() , and 10 discriminants, starting with
, and 10 discriminants, starting with![]() , such that
, such that ![]() is of non-elementary type
is of non-elementary type![]() . For the single discriminant
. For the single discriminant![]() , we have a 3-class group of type
, we have a 3-class group of type![]() . We have published this information in the Online Encyclopedia of Integer Sequences (OEIS) [39] , sequences A244574 and A244575.
. We have published this information in the Online Encyclopedia of Integer Sequences (OEIS) [39] , sequences A244574 and A244575.
7.2. Arithmetic Invariants of Fields ![]() with
with ![]()
After the preliminary data collection in Section 7.1, we restrict ourselves to the 14 cases with elementary abe-
lian 3-class group of type![]() . The complex quadratic field
. The complex quadratic field ![]() possesses 13 unramified cyclic
possesses 13 unramified cyclic
cubic extensions ![]() with dihedral absolute Galois group
with dihedral absolute Galois group ![]() of order six [23] . Based on Fieker’s technique [40] , we use the computational algebra system MAGMA [3] [4] to construct these extensions and to calculate their arithmetical invariants. In Table 2, which is continued in Table 3 on the following page, we present the kernel
of order six [23] . Based on Fieker’s technique [40] , we use the computational algebra system MAGMA [3] [4] to construct these extensions and to calculate their arithmetical invariants. In Table 2, which is continued in Table 3 on the following page, we present the kernel ![]() of the 3-principalization of
of the 3-principalization of ![]() in
in ![]() [21] [23] , the occupation numbers
[21] [23] , the occupation numbers ![]() of the principalization kernels [19] , and the abelian type invariants
of the principalization kernels [19] , and the abelian type invariants![]() , resp.
, resp.![]() , of the 3-class group
, of the 3-class group![]() , resp.
, resp.![]() , for each
, for each ![]() [5] [9] . Here, we denote by
[5] [9] . Here, we denote by ![]() the unique real non-Galois absolutely
the unique real non-Galois absolutely
![]()
Table 2. Pattern recognition via ordered IPADs.
![]()
Table 3. Pattern recognition (continued).
cubic subfield of![]() . For brevity, we give 3-logarithms of abelian type invariants and we denote iteration by formal exponents. Note that the multiplets
. For brevity, we give 3-logarithms of abelian type invariants and we denote iteration by formal exponents. Note that the multiplets ![]() and
and ![]() are ordered and in componentwise mutual correspon- dence, in the sense of
are ordered and in componentwise mutual correspon- dence, in the sense of ![]() 4.
4.
In Table 4, we classify each of the 14 complex quadratic fields ![]() of type
of type ![]() according to
according to
the counters of the abelian type invariants of the 3-class groups ![]() of the 13 unramified cyclic cubic extensions
of the 13 unramified cyclic cubic extensions![]() , that is the accumulated (unordered) form of the IPAD of
, that is the accumulated (unordered) form of the IPAD of![]() . Whereas the dominant part of these groups is of order
. Whereas the dominant part of these groups is of order![]() , there always exist(s) at least one and at most four distinguished groups of bigger order, usually
, there always exist(s) at least one and at most four distinguished groups of bigger order, usually ![]() and occasionally even
and occasionally even![]() . According to the number of distinguished groups, we speak about uni-, bi-, tri- or tetra-polarization. If the maximal value of the order is
. According to the number of distinguished groups, we speak about uni-, bi-, tri- or tetra-polarization. If the maximal value of the order is![]() , then we have a ground state, otherwise an excited state.
, then we have a ground state, otherwise an excited state.
7.3. Proof of Theorem 7.1
Proof. According to ( [9] , Thm.1.1 and Dfn. 1.1, pp. 402-403), the information given in Table 4 consists of iso- morphism invariants of the metabelian Galois group ![]() of the second Hilbert 3-class field of
of the second Hilbert 3-class field of ![]() [23] . Consequently, with respect to the 13 abelian type invariants of the 3-class groups
[23] . Consequently, with respect to the 13 abelian type invariants of the 3-class groups ![]() alone, only the groups
alone, only the groups ![]() for
for ![]() could be isomorphic. However, Table 2 and Table 3 show that these three groups differ with respect to another isomorphism invariant, the 3-principalization type
could be isomorphic. However, Table 2 and Table 3 show that these three groups differ with respect to another isomorphism invariant, the 3-principalization type ![]() [19] [21] , since the corresponding maximal occupation numbers of the multiplet
[19] [21] , since the corresponding maximal occupation numbers of the multiplet ![]() are
are![]() , respectively. □
, respectively. □
7.4. Final Remark
We would like to emphasize that Theorem 7.1 provides evidence of a wealth of structure in the set of infinite 3-class field towers, which was unknown up to now, since the common practice is to consider a 3-class field tower as done when some criterion in the style of Golod-Shafarevich-Vinberg [31] [36] [37] or Koch-Venkov [32] ensures just its infinity. However, this perspective is very coarse and our result proves that it can be refined considerably.
It would be interesting to extend the range of discriminants ![]() and to find the first examples of isomorphic infinite 3-class field towers.
and to find the first examples of isomorphic infinite 3-class field towers.
![]()
Table 4. Accumulative (unordered) form of IPADs.
Another very difficult remaining open problem is the actual identification of the metabelianizations of the 3-tower groups ![]() of the 14 fields. The complexity of this task is due to unmanageable descendant numbers of certain vertices, e.g.
of the 14 fields. The complexity of this task is due to unmanageable descendant numbers of certain vertices, e.g. ![]() and
and![]() , in the tree with root
, in the tree with root![]() .
.
Acknowledgements
We gratefully acknowledge that our research is supported by the Austrian Science Fund (FWF): P 26008-N25. The results of this paper will be presented during the 29th Journées Arithmeétiques at the University of Debrecen [41] .
Funding
Research supported by the Austrian Science Fund (FWF): P 26008-N25.