1. Introduction
Most economic models are expressed in terms of prices and quantities. In practice, however, economic data is often available only in terms of revenues or expenditures (value data). Value data is the product of prices and quantities, but does not provide explicit price and quantity information. Cobb and Douglas [1] and Farrell [2] are two canonical examples using such data. Shephard [3] developed duality theory to utilize value data1. However, his results depend on price information.
Bowley [4] introduced a ratio-based price index, calculated as the geometric mean of the Paasche and Laspeyres indexes2. Fisher [5] identified it as “ideal” for satisfying a set of mathematical properties, collectively the Test Approach (see Fisher [6] ), and emphasized its use as a quantity index. Konüs [7] showed Fisher’s ideal index to be an exact solution for a quadratic production function. Diewert [8] demonstrated its exactness for a flexible second-order quadratic mean aggregator (utility or production) function, showing it to be superlative and completing the Economic Approach. Finally, Diewert [9] extended its use to Malmquist [10] output, input, and productivity indexes.
In a separate line of inquiry, Afriat [11] exploited properties of the Weak Axiom3 (Cyclical Consistency) to recover unobserved utility from consumer-level price and quantity data and later unobserved technology from production prices and quantities [12] . Cross and Färe [13] extended Afriat’s approach, using nonlinear programing to recover unobserved price relatives from firm-level revenues and expenditures.
Balk [14] uses dimensional invariance to construct Fisher ideal price and quantity indexes with value data and price relatives, instead of prices and quantities. Statistical agencies utilize this method, augmenting value data with secondary price surveys and constructing elementary price indexes [14] .
In this article, we show how to construct Fisher ideal price indexes directly from value data, without price relatives or the secondary price survey. In the next section, we review the value-based Fisher index, expressed in terms of value data and price relatives. We then recover the Fisher index price relatives from value data, without prices. In Section 3, we evaluate the accuracy of our value-based index in a simple Monte Carlo experiment in which firms respond rationally, but not optimally, to price changes. We then conclude.
2. A Value-Based Fisher Index
Let 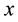 and
and 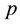 be vectors of (input) quantities and their prices, and denote output/utility
be vectors of (input) quantities and their prices, and denote output/utility  and the production/utility function
and the production/utility function
 . (1)
. (1)

3We use the term Weak Axiom of Profit Maximization (Weak Axiom) discussed by Varian [15] , though many alternatives exist, notably Afriat’s [11] Cyclical Consistency.
4For the existence of a minimum, see Färe and Primont [16] . Note that 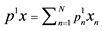 is the inner product of prices and quantities.
is the inner product of prices and quantities.
5Constant price relative across firms is a weaker restriction than constant prices, the so called “Law of One Price” [17] .
The cost function4 is defined
 . (2)
. (2)
Konüs [7] defines a price index for situations 0 and 1 as the ratio of cost functions,
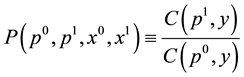 . (3)
. (3)
Here, the price index is defined for a fixed output level .
.
Consider a unit cost function  which is homogeneous, quadratic mean of order
which is homogeneous, quadratic mean of order . Here
. Here 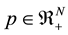 is the price vector for goods
is the price vector for goods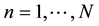 . According to Diewert [9] , this cost function is flexible, since it can provide a second order differential approximation to any linearly homogeneous, twice continuously differentiable, positive function. When a price function is exact for a flexible function, like the quadratic mean, it is said to be superlative.
. According to Diewert [9] , this cost function is flexible, since it can provide a second order differential approximation to any linearly homogeneous, twice continuously differentiable, positive function. When a price function is exact for a flexible function, like the quadratic mean, it is said to be superlative.
The Fisher index  is exact for a second-order Quadratic cost function
is exact for a second-order Quadratic cost function . It is the geometric mean of two component indexes. The Laspeyres index
. It is the geometric mean of two component indexes. The Laspeyres index  is a ratio of prices, weighted by past period quantities
is a ratio of prices, weighted by past period quantities![]() , whereas, the Paasche index
, whereas, the Paasche index ![]() is weighted by current period quantities
is weighted by current period quantities![]() :
:
![]() (4)
(4)
The Fisher is then![]() .
.
Following Balk [14] , we can write the value-based Fisher index ![]() in terms of value data
in terms of value data ![]() and price relatives
and price relatives ![]() for situations 0 and 1, constant across firms5,
for situations 0 and 1, constant across firms5,
![]() . (5)
. (5)
The expenditure share is given by![]() , and
, and ![]() is the input quantity vector.
is the input quantity vector.
3. The Programming Problem
We wish to recover price information from the inner product of price and quantity![]() . It is well known that prices and price relatives cannot be recovered from the inner product alone, since it is an under- identified system of 2N equations and 4N unknowns:
. It is well known that prices and price relatives cannot be recovered from the inner product alone, since it is an under- identified system of 2N equations and 4N unknowns:
![]() (6)
(6)
Here, all inputs and outputs are included ![]() for situations 0 and 1.
for situations 0 and 1.
Identification is trivial when firms are strictly cost minimizing and the technology ![]() is known a priori. To see why, suppose the cost function
is known a priori. To see why, suppose the cost function ![]() is differentiable in
is differentiable in![]() . By Shephard’s lemma, the solution vector
. By Shephard’s lemma, the solution vector ![]() is a function of prices, and the value vector is an exactly identified system of 2N (possibly nonlinear) equations and 2N unknowns,
is a function of prices, and the value vector is an exactly identified system of 2N (possibly nonlinear) equations and 2N unknowns,
![]() . (7)
. (7)
Price relatives may still be recovered from this system when firms are not strictly cost minimizing, but are instead weakly rational. To illustrate how this is possible, consider first an economy in which there is no quantity response to price change, due to some regulation, capital constraint, or information asymmetry. The response vector ![]() is exactly zero
is exactly zero ![]() for each firm in the economy. Exact price relatives
for each firm in the economy. Exact price relatives ![]() are recoverable directly from the
are recoverable directly from the ![]() value ratios of any perfectly constrained firm:
value ratios of any perfectly constrained firm:
![]() . (8)
. (8)
This economy is not cost minimizing, but satisfies Afriat’s [12] Weak Axiom of Profit Maximization,
![]() . (9)
. (9)
In fact, the perfectly constrained firm defines the null vector 0 of Weak Axiom’s convex response-cone, and the profit maximizing firm defines its upper bound, illustrated in Figure 1.
![]()
Figure 1. Monte Carlo example-production response with error.
Under dimensional invariance (see Balk [14] ), the inequality (9) can be rewritten in value and price relative terms:
![]() (10)
(10)
The vector of shadow price relatives ![]() then solves the minimization problem, given values for firms
then solves the minimization problem, given values for firms![]() ,
,
![]() (11)
(11)
4. Monte Carlo
To explore the accuracy of the proposed value-based Fisher index, we simulate a two-period, two-input, unit output economy and recovered price relatives ![]() from problem (11). Firms respond to input price changes rationally, but incompletely in both magnitude and direction, as illustrated in Figure 1.
from problem (11). Firms respond to input price changes rationally, but incompletely in both magnitude and direction, as illustrated in Figure 1.
Both response magnitude and direction are random variables, following two independent 2-parameter Beta distributions, with identical shape parameter sets![]() . Response magnitude ranges between zero and the cost minimizing response to problem (2). Response direction has compact support from the rationalizing price cone formed by price line
. Response magnitude ranges between zero and the cost minimizing response to problem (2). Response direction has compact support from the rationalizing price cone formed by price line ![]() and shifted price line
and shifted price line![]() . Such responses lead to Farrell [2] technical and allocative inefficiency bounded by the Weak Axiom.
. Such responses lead to Farrell [2] technical and allocative inefficiency bounded by the Weak Axiom.
Define accuracy ![]() of price index
of price index ![]() as the ratio of the value-based price index with recovered price relatives
as the ratio of the value-based price index with recovered price relatives ![]() and the full information price index:
and the full information price index:![]() . Then,
. Then, ![]() is accurate. Value-based indexes overstate price changes when
is accurate. Value-based indexes overstate price changes when ![]() and understate when
and understate when![]() . All statistics are reported for 300 iterations.
. All statistics are reported for 300 iterations.
4.1. Technology
We consider a Translog unit cost function and impose parameter restrictions![]() , for
, for![]() , corresponding to the Cobb-Douglas cost function, for which the Törnqvist-Theil and Jevons indexes are exact, and
, corresponding to the Cobb-Douglas cost function, for which the Törnqvist-Theil and Jevons indexes are exact, and ![]() (homogeneity). The response vector’s cost-minimizing upper bound is derived by setting the expenditure share identity
(homogeneity). The response vector’s cost-minimizing upper bound is derived by setting the expenditure share identity ![]() equal to the optimal expenditure share
equal to the optimal expenditure share![]() .
.
4.2. Results
Table 1 reports accuracy levels for the value-based Fisher index and its two elementary components for firm sample sizes increasing from 15 to 30 firms, with a 200% increase in the second input price. Price response variation (standard deviation) ranges from 0.14 to 0.41, corresponding to shape parameter ![]() from 0.5 to 6.0.
from 0.5 to 6.0.
The value-based Fisher index is understated, ![]() , for higher sample sizes
, for higher sample sizes ![]() and higher price response variation (standard deviation
and higher price response variation (standard deviation![]() ) and overstated otherwise. Overall, accuracy improves with higher sample sizes and higher price response variation.
) and overstated otherwise. Overall, accuracy improves with higher sample sizes and higher price response variation.
Value-based Paasche and Laspeyres component indexes are under and overstated, respectively, at all levels of volatility and price deviations. This is reasonable, because they reference only a single-period market basket, whereas the Fisher index averages over the two-period market basket.
Table 2 illustrates accuracy levels for a range of price increases, from 50% to 200%, and three volatility levels. Firm sample size K is 15. The value-based index is overstated for larger price increases ![]() and lower price response variation (St. Dev.
and lower price response variation (St. Dev.![]() ).
).
5. Conclusion
Economic data are frequently available in value terms, rather than price and quantity terms. We extended the superlative Fisher index to value data and recovered price relatives by exploiting the Weak Axiom. Our value-
![]()
Table 1. V-price index accuracy for a 200% price increase, reported for three firm sample sizes and three firm-response standard deviation levels.
![]()
Table 2. V-price index accuracy for 15 firms, reported for three price relatives (percentage increase) and three firm-response standard deviation levels.
based Fisher model eliminates the need for supplementary price information. The value-based model’s accuracy is encouraging, when firms respond to price changes rationally, but with error. We did not explore econometric approaches to price recovery. We also did not explore the accuracy of the value-based model when firms respond irrationally to price changes, violating the Weak Axiom. Such would be the case when the response error term is two-sided. Both extensions would be of practical interest.
Acknowledgements
Authors thankfully acknowledge Bert Balk’s extensive criticisms and suggestions for this project.
NOTES
*Corresponding author.
1Shephard [3] notes: “Statistical studies of cost functions are generally more accessible than corresponding empirical investigations of production functions, because economic data are most frequently in price and monetary (value) terms.”
2Fisher [6] acknowledges (page XV) Bowley’ [4] early identification (page 641) of the “ideal” index in an addendum added shortly before going to press in October, 1922.