1. Introduction
Gaseous nebulae are often parameterized by an external radiation field, generally from nearby star or stars. The particles (atoms, ions and electrons) in the nebulae and the photons of radiation field interact in such way that the physical properties of the nebulae can be deduced by studying the net light coming from the model. To model the theoretical spectrum that we would expect to see from a specific nebula, it is necessary to have detailed knowledge of the microscopic processes occurring within the nebulae [2] . The gaseous nebulae and photons pass through in the radiation atomic processes. All of these processes reach in equilibrium of photoionization and recombination of ions and particles.
In this paper, we use photoionization models in conjunction with high spatial resolution data to develop a framework for interpreting H II region spectra. The contents, physics and basic numerical framework of codes are explained in “Hazy: A brief introduction to the code”. The paper presented here applies version of CLOUDY C10.00 of the code [3] .
CLOUDY is a well-known and widely used photoionization code which is available at http://www.pa.uky.edu/gray/cloudy. This code is used for modelling ionized region. It also helps to calculate the structure of grains in photo dissociation region (PDR). In this work, we only focus on the ionization structure of oxygen, hydrogen and helium, and the temperature of electron in the absence of grains.
The main goal of this work is to develop model of the photoionization of gaseous nebula and assess the impacts of heavy metals like C, O, S, Ne and N by assuming low density (optically thin) plasmas found in the nebulae, based on specific assumptions given below to study the ionization structures of oxygen ions, hydrogen, helium, intensity ratios of [OI]l6300, [O3]l5007; 4959 with Ib and temperature of electron by changing the abundances of oxygen from −5.0 ≤ log(O/H) ≤ −2.5 in step of 0.5 dex keeping the abundances of carbon relative to hydrogen changes by 0.5, 0.25 dex to avoid CO formation in the process, whereas the abundances of the other elements are the same as shown in Table 1.
This paper is organized as follows. Section 2 gives a brief overview on the physical properties of the gas. In Section 3, we describe the codes used to model theoretical evolution of heavy metals and the ionization of the surrounding nebulae. In Section 4, we analyse the result obtained in Section 3, and finally, we summarize the main result in the last section.
2. Physical Properties of the Gas
In the photoionization equilibrium, the number of ionization of neutral hydrogen is balanced by the number of recombinations. The nebular of ionizations can easily be calculated from the ionizing spectrum, and the number of recombinations can be computed in hydrogen recombination lines that hardly depend on the plasma parameters.
The emission line spectrum of an ionized nebula depends on the combination of the ionizing spectrum, the chemical composition of the so called ionization parameter U. The elemental abundances of the gas have been made consistent with the metallicity of the ionizing stars. The solar abundances were scaled here are given in Table 1. We are assuming solar elemental abundances given by [4] .
In ionization bounded nebula purely composed of hydrogen, the total number of recombinations per unit time balances the total number of photons with energies above 13.6 eV emitted per unit time either by the star, or during recombination to the ground level. It has given by [5] as
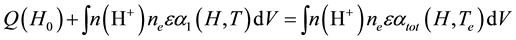 (1)
(1)
where Q(H0) is the total number of photons with energies above 13.6 eV emitted by the star per second; 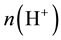 is the number density of H ions, ne is the electron density,
is the number density of H ions, ne is the electron density, 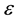 is the volume filling factor of the nebular gas;
is the volume filling factor of the nebular gas; 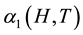 is the H recombination coefficient to the ground level while
is the H recombination coefficient to the ground level while 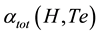 is the total H recombination coefficient, which are both roughly inversely proportional to the electron temperature Te. The integrations are performed over the nebular volume. The ionization parameter is related to flux, hydrogen number density,
is the total H recombination coefficient, which are both roughly inversely proportional to the electron temperature Te. The integrations are performed over the nebular volume. The ionization parameter is related to flux, hydrogen number density,
![]()
Table 1. The log values of elemental abundances relative to hydrogen.
and radius to the model slabs inner faces by the formula
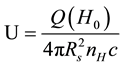 (2)
(2)
where c is the speed of light, and RS is the Stromgren radius (i.e. the radius of the ionization front), QH is the number of ionizing photons per second and is given by
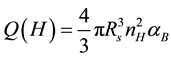 (3)
(3)
where 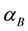 is the case B temperature dependent recombination coefficients. The thickness of the transition region between the fully ionized zone and the neutral zone is approximately one mean free path of an ionizing photon
is the case B temperature dependent recombination coefficients. The thickness of the transition region between the fully ionized zone and the neutral zone is approximately one mean free path of an ionizing photon
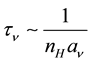 (4)
(4)
where 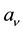 is the hydrogen photo-ionization cross section at the typical frequency of the photons reaching the ionization front. This thickness is generally much smaller than the size of the nebula and justifies the concept of a Stromgren sphere [6] . There is however cases when the transition region might be extended, such as in diffuse media or when the ionizing radiation field contains a large amount of X-ray photons (which are less efficiently absorbed by hydrogen). We plug Equations (2) and (3) together, we obtain the ionization parameter U is proportional to the Stomgren radius, i.e.
is the hydrogen photo-ionization cross section at the typical frequency of the photons reaching the ionization front. This thickness is generally much smaller than the size of the nebula and justifies the concept of a Stromgren sphere [6] . There is however cases when the transition region might be extended, such as in diffuse media or when the ionizing radiation field contains a large amount of X-ray photons (which are less efficiently absorbed by hydrogen). We plug Equations (2) and (3) together, we obtain the ionization parameter U is proportional to the Stomgren radius, i.e.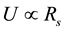 .
.
3. Model
In our model of H II regions, the intensity ratio are sensitive to different parameters: the abundance of the element, the temperature of the radiation supplied by the ionizing stars, the ionization parameter, U, effectively the relative density of ionized at each point on the nebulae; and the oxygen abundances, since in the abundance range of interest Te, and hence the collision excitation rate, are regulated by forbidden line radiation from O2+ and O+ ions. Here we wish to examine the relationship between oxygen abundances and the temperature and intensity of ionizing radiation, it is necessary to explore the (O/H, Te, U) parameter space. The volume which must be searched can be limited by using the estimate O/H obtained from Te (O2+) and by assuming H II regions are ionized by clusters of massive O stars.
3.1. Model Parameters
Only few parameters need to be specified to predict the spectrum of a photoionized cloud: the shape of the radiation field emitted by central object, the flux of photons striking the illuminated face of the cloud, the ionization parameter, U, effectively the relative density of ionizing particles to be ionized at each point in the nebulae. These are important parameters to develop the model. As we discussed in Section 2, the element considered for the nebular heating (by photoionization), cooling, and opacity are H, He, N, O, C, Ne and S. These will be referred to as “primary elements”. These determine the electron temperature, ionization structure, and radiation field at all points in the nebulae. The construction of a model nebula depends on the abundances of these elements shown in Table 1. The other parameters of the nebular gas are the mean density and its distribution usually taken to be uniform.
3.2. Summary of the Model
Photoionization modelling, however, generally does not take into account the presence of dust, which can absorb Lyman continuum photons before they even have a chance to ionize the gas and remits them in infrared. We have the following assumptions and the method we strictly follow to study this problem. The model for Photoionization is quite simple and comprises the following basic assumptions.
1) The ionization parameter U varies from −2.0 ≤ log(U) ≤ −1.0, this is more appropriate for low density and it is a dimensionless ratio of hydrogen ionizing photon to total hydrogen density.
2) The nebular is spherically symmetric.
3) The hydrogen number density is uniform and has value of 1000 cm3.
4) The filling factor is 0.1.
5) The region is assumed to be static sphere, completely surrounding the central star and letting no inward directed diffuse line or continuum radiation escape.
6) The inner radius R is fixed variable but the outer radius of the nebula is not fixed as an input parameter.
7) The ionization bounded, with the calculation stopped at a gas temperature of 100 K.
8) We also include a grid of Photoionization for the emission from the interface between the ionized gas and molecular clouds in the region.
9) We can assume that the region is optically thin and that the “on-the-spot” assumption is valid.
10) We ignore any dynamics, for turbulence and the effects of block and ionization fronts.
The above assumptions leave the following free parameters: the stellar temperature, the luminosity of the central in the ionized region. To model Photoionization of gaseous, we use a modified version of the Photoionization code CLOUDY C10:00 [3] .
4. Model Result
Here we present the results of our calculations, spanning a wide range of U, and n(H) hydrogen density. The result depicts in Figure 1 the H and He ionization profiles calculated for the standard model developed here. The fractional abundances of each ionic species of H and He that is the ratio of the abundance of its parent element, is shown in (Figure 1(a) and Figure 1(b)). The H+ and H0 profiles cross at a radius of 1.9 × 1018 cm, and each species having equal fractional abundances of at this radius. The helium ions He2+ and He+ profiles cross a radius of 0.8 × 1018 cm with fractional abundances of 50% each. On this distance onwards, He+ dominate the region but the recombination rate is so fast, the helium atom start to dominate from 2 × 1018 cm.
During the photoionization process, the absorption of photon creates a free electron with the other electrons present in the gas by elastic collisions, and thus heats the gas. The energy gains are usually atoms, although photo-ionization of helium contributes significantly. Intuition might suggest that Te the ionizing source, since the ionizing radiation field decreases because of geometrical dilution and absorption in the intervening layers. Figure 2 depicts the variation of electron temperature with distance. It also shows that the temperature of electron falls down to temperature of 8000 K and raise slowly to 1 × 104 K and falls down continuously.
Figure 3 depicts the ionization structure of both hydrogen and helium when the ionization parameter is −2.0. We have seen the sharp outer edge of the He2+ zone, as well as the even sharper outer edges of the H+ and He+ zones can be seen in the graphs. The differences are when the ionization parameter is decreases, the recombination rate in the inner region of He2+, the stellar radiation with hν > 54.4 eV is absorbed only by the He+, this occurs to until He+ dominate the processes. Figure 4 shows depict the electron temperature profiles with the distance. It shows that the electron temperature slowly declines and rises to peak values and drop down to the least temperature. This is due to the cooling effect of oxygen ions.
![]()
Figure 1. Calculated profiles of the ionized region for the model ionization parameter log(U) = −1.5 and n = 1000 cm−3. (a) Fractional abundances of neutral and ionized hydrogen; (b) Fractional abundances of neutral, single and double ionized helium.
![]()
Figure 2. Calculated profiles of the ionized region for the model ionization parameter log(U) = −1.5 and n = 1000 cm−3 temperature of electrons profile.
![]()
Figure 3. Calculated profiles of the ionized region for the model ionization parameter log(U) = −2.0 and n = 1000 cm−3. (a) Fractional abundances of neutral and ionized region; (b) Fractional abundances of neutral, single and double ionized helium.
Figure 5 depicts the ionization structure of oxygen families. We apply charge transfer reaction to study this structure. Charge transfer reactions can be very important for the ionization structure of a wide range of astrophysical plasma [7] . This is kind of reaction presents a crucial interest in model of photoionized nebulae. In the interstellar medium, charge transfer reaction leads the ionization structure of elements like oxygen ionized by temperature below 1 × 104 K. The charge transfer reaction between oxygen ion and hydrogen atom given by play significant role in regulating the degree of ionization of various ions which are abundant in the interstellar medium [8] .

It depicts in Figure 5, the ionization structure of all the possible ions formed by the ionization parameter log(U) = −2.0, given in the model for two different cases such as transfer and no transfer of charge through the
![]()
Figure 4. Calculated temperature profiles of the ionized region for the model ionization parameter log(U) = −2.0 and n = 1000 cm−3.
![]()
Figure 5. Calculated profiles of the ionized region for the model ionization parameter log(U) = −2.0 and n = 1000 cm−3: fractional abundances of O I, O II, O III, O IV, O V ions.
processes. O II rapidly recombines with hydrogen because of charge transfer interaction between hydrogen atoms. There is a recombination of ions between O III and O IV but in the presence of charge transfer the rate of recombination is high relative to the absence. O V and O VI ionization structures are almost the same and dependence of charge transfer is almost negligible and recombined rapidly. In both cases the ionization structure of oxygen ions decreasing with the increasing distance from the centre and the optical depth extends up to 0.165 pc, where the oxygen ion (O+) is totally recombined to oxygen atoms.
As we described in the model, we were aiming to explore the function of (log(O/H), Te, U and fluxes with respect of H ). The result shown in Table 2 clearly describes this phenomenon. The parameters are listed all depend on the abundances of oxygen.
The modified peak temperatures and electron density are indicated in the Figure 6 are coming from the second and third rows of Table 2 for the ionization parameter, log(U) = −2.0. We believed that both temperature and electron density depend on the abundances. We tries to show that the electron temperature inside the cloud and electron number density versus the oxygen abundances. We see that the change of electron temperature is almost constant when the abundances changes from −5 to −3.5 and falls rapidly when the log(O/H) changes to −2.5. The change of peak electron number density with abundances of oxygen is almost insignificant and its relative change is 0.25%.
Figure 7 shows when the abundances of oxygen, log(O/H) = −4.0, the line flux ratio, i.e. ![]() has
has
![]()
Table 2. Elemental abundances of oxygen and carbon used in this model, the line ratio of oxygen with the Iβ and temperatures of both.
![]()
Figure 6. Peak temperature and electron number density with the abundances of oxygen when the ionization parameter log(U) = −2.0.
a peak value. Moreover, the model shows that when the abundances of O/H increases, line ratio increases in most of the lines, and drops when it is near to log(O/H) = 2.5.
Figure 8 shows the function of log(O/H) with TeO2+ and T(H+). The result depicts that in all cases the TeO2+ is greater than T (H+). They decrease with increase of the abundances. This is due to thermal effect of the forbidden line radiation from O2+ and O+.
![]()
Figure 7. Excitation of oxygen fluxes lines vs oxygen abundances from the electron temperature with ionization parameter, log(U) = −2.0.
![]()
Figure 8. Temperature of oxygen ion and hydrogen ions vs oxygen abundances from the electron temperature with ionization parameter, log(U) = −2.0.
5. Conclusion
In this work, we have presented photoionization model of gaseous nebula. Our current study indicates that we could use the photoionization modelling to obtain the ionization structure of hydrogen, helium and temperature for oxygen ions with some of the assumption described in Section 3.1. We are carrying out such an exercise to study the structure of oxygen ions in the presence and absence of charge transfer between hydrogen and oxygen ion. The rate of charge transfer has a significant role on the structure. The result also shows that ionization
![]()
Table 3. Elemental abundances of oxygen and carbon used in this model, the line ratio of oxygen with the Iβ and temperatures of both O [III] and [H II].
structure of oxygen when the charge transfer takes place is more rapid than the absence of charge transfer. In addition to this, ionization parameters are crucial in affecting the model. Moreover, in this paper we attempted to explain the intensities ratio with Iβ in the framework of photoionization model. The line ratio with Iβ depends with oxygen abundances of the nebulae. The transfer of charge also affects the temperature of electrons and the ionization structure of the elements. We have deducted from Table 2 and Table 3, the dependence of the lines ratio, T[O2+], T(H+), Te and ne with the abundances of oxygen and carbon relative to hydrogen.
Acknowledgements
I would like to thank my supervisor Prof. Dreck Smith for his useful discussion during the progress of this work. Also thanks to my brother Sisay Bizuneh for his real support.