A Review of Measurement-Integrated Simulation of Complex Real Flows ()
1. Introduction
Recent advances in computational fluid dynamics (CFD) enable calculation of complex flows appearing in many practical applications with reasonable accuracy. However, an accurate solution usually does not mean a solution that reproduces the exact instantaneous structure of the real flow such as a turbulent flow, but rather one having the same statistical characteristics as those of the relevant flow [1] . It is quite difficult to obtain the exact flow solution because: 1) it is difficult to specify the initial and/or boundary conditions of real flows correctly; and 2) even if these data are available, a small error in the initial condition will increase exponentially in structurally unstable dynamical systems such as turbulent flows [2] .
In spite of the inherent difficulty, reproducing the exact structure of real flows is a critically important issue in many fields, such as weather forecasting or feedback flow control. In numerical simulation used for weather forecasting, the initial condition is updated at time intervals based on past computational results and measurement data around the computational grid points. In meteorology, extensive studies have been carried out on such methods, which are termed data assimilation [3] . The four-dimensional variational method (4D-Var) is widely used in numerical weather forecasting [4] -[6] , but it requires huge computational power to repeatedly solve flow dynamics and its adjoint, and, therefore, is not suitable for application to problems of real-time flow reproduction such as feedback flow control. A similar concept, namely, interactive computational-experimental methodology (ICEME), was proposed by Humphrey [7] for application to engineering problems, in which the measurement data are supplied to a thermal-flow simulation to enhance the efficiency of computation. Possible advantages of ICEME as well as further necessary studies were discussed in relation to a complex flow-related optimization problem seeking the optimum arrangement of electrical heat sources to minimize the temperature in a ventilated box under some constraints. Zeldin and Meade [8] applied the Tikhonov regularization method, which is common in inverse problems, to obtain an optimum solution for estimation of the real flow from the numerical and measurement results of the relevant flow. Particle imaging velocimetry (PIV) has proved to be a mature method to obtain velocity vectors in a flow domain. Studies have been made on the application of CFD schemes to modify PIV measurement so as to satisfy physical constraints such as the continuity equation [9] . State observer, which is a fundamental methodology in modern control theory to estimate the state variables from the state equation with the aid of partial measurement data, has been used in flow problems. Uchiyama and Hakomori [10] reproduced the unsteady flow field in a pipe using a Kalman filter, which is a special state observer [11] . Högberg et al. [12] constructed a Kalman filter to estimate the flow state from the information on the wall in a numerical experiment for the optimum control of the subcritical instability of a channel flow based on a linearized equation. The Kalman filter and state observer seek the asymptotic convergence to the optimum state requiring only one forward integration from an arbitrary initial condition. Having much less computational load, they are potential candidates to solve the problem of how to reproduce real flows. Comparison of the Kalman filter and state observer shows that the latter has a simpler structure and retains an essential part of the state estimation. The present author [13] proposed a measurement-integrated simulation (hereafter abbreviated as “MI simulation”), which is a kind of observer using a CFD scheme as the mathematical model of a relevant system, and successfully applied it to a turbulent flow in a square duct, a Karman vortex street behind a square cylinder [14] [15] , and blood flow in an aneurismal aorta [16] .
Measurement-integrated simulation is a state observer for a flow field. An observer is a common tool in control theory to estimate the real state from a mathematical model and partial measurement [17] . As shown in the block diagram in Figure 1, the real system (“Physical flow” in the figure) is modeled as a differential equation (“Model flow”). Computation is performed using sequential measurement data, and the difference between the outputs of the computation and measurement, or the estimation error, is fed back to the model through the feedback law. This feedback signal modifies the dynamical structure of the model system and the properly designed feedback law results in an asymptotic reduction of the estimation error even if initial conditions (“I. C. (1)” and “I. C. (2)”) of physical and real flows are different. In observable linear systems, convergence of the output signal guarantees coincidence of all state variables. In design of the observer, determination of the mathematical model and that of the feedback law are the key factors. For finite dimensional linear dynamical systems satisfying observability condition, the observer of an arbitrary exponential convergence property can be designed by the standard pole placement technique [16] . A Kalman filter is also a kind of observer in which the feedback gain is determined to minimize the cost function in consideration of the statistical behavior of the measurement in stochastic dynamical systems [10] . Extension of the observer for application to nonlinear systems has been studied extensively for finite dimensional cases [18] . For infinite dimensional linear systems, the state observer is designed in the same manner as in finite dimensional cases and implemented after finite-dimensional approximation [19] . However, a general theory of the observer applicable to infinite-dimensional and nonlinear dynamical systems such as flows has not yet been established [20] . As a methodology to reproduce real flows, the authors have proposed an MI simulation. The main feature of this MI simulation, which distinguishes it from
![]()
Figure 1. Block diagram of measurement-integrated (MI) simulation.
other existing observers, is the usage of a CFD scheme as a mathematical model of the physical flow. A large dimensional nonlinear CFD model makes it difficult to design the feedback law in a theoretical manner; therefore, it has been determined by a trial-and-error method based on physical considerations. However, it makes it possible to accurately reproduce real flows once the feedback law is properly designed.
This review article deals with the theoretical background and applications of MI simulation. In Section 2, formulations of MI simulation are presented, including governing equations of an observer for a flow field, those of a linearized error dynamics describing the convergence of the observer [21] , and stabilization of the numerical scheme, which is important in implementation of MI simulation [22] . Applications of MI simulation presented in Section 3 range from fundamental turbulent pipe flows [1] [13] [23] and Karman vortices in a wind tunnel [14] [24] to clinical application to diagnosis of blood flows in a human body [16] [25] -[27] .
2. Formulation of Measurement Integrated Simulation
2.1. Governing Equations
Measurement-integrated simulation deals with incompressible and viscous fluid flow. The dynamic behavior of the flow field is governed by the Navier-Stokes equation:
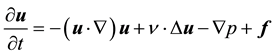 (1)
(1)
and the equation of mass continuity:
 (2)
(2)
as well as by the initial and boundary conditions. In the Navier-Stokes Equation (1), p denotes the pressure divided by density, and f denotes the body force divided by density which is defined as the feedback signal in the MI simulation. The pressure equation is derived from Equation (1) and (2) as
 (3)
(3)
We use Equations (1) and (3) as the fundamental equations.
The basic equation of the MI simulation is represented as a spatially discretized form of governing equations (1) and (3):
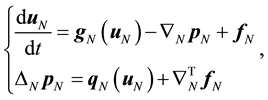 (4)
(4)
where uN and pN are computational results for the 3N-dimensional velocity vector and the N-dimensional pressure vector, respectively, N denotes the number of grid points, gN, qN, ∇N and ΔN are matrices which express the discrete form of operators g, q, ∇, and Δ. The operators, g and q are defined as follows
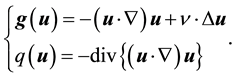 (5)
(5)
It is noted that effects of the boundary conditions are included in the functions gN and qN.
We define the operator 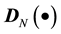 to generate the N-dimensional vector consisting of the values of a scalar field sampled at N grid points. The definition of DN is naturally extended to the case when the variable is a velocity vector field as
to generate the N-dimensional vector consisting of the values of a scalar field sampled at N grid points. The definition of DN is naturally extended to the case when the variable is a velocity vector field as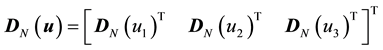 . Applying the operator to the Navier Stokes equation and the pressure equation, we obtain the sampling of these equations at N grid points.
. Applying the operator to the Navier Stokes equation and the pressure equation, we obtain the sampling of these equations at N grid points.
On the other hand, we apply external force denoted by a function of real flow and numerical simulation in MI simulation. In this study, we consider the case in which external force fN is denoted by a linear function of the difference of velocity and pressure between real flow and numerical simulation:
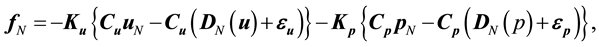 (6)
(6)
where Ku denotes the 3N-by-3N feedback gain matrix of velocity, Kp denotes the 3N-by-N feedback gain matrix of pressure, Cu and Cp denote the 3N-by-3N and N-by-N diagonal matrices consisting of diagonal elements of 1 for measurable points or 0 for immeasurable points, and 3N-dimensional vector εu and N-dimensional vector εp mean measurement error. By introducing Equation (6) into Equation (4), we derive the general formulation of MI simulation:
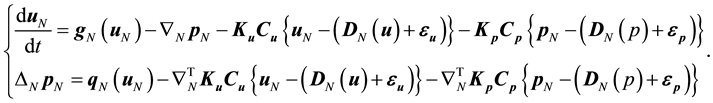 (7)
(7)
2.2. Linearized Error Dynamics
We now derive the linearized error dynamics of MI simulation. Disregarding the second order and higher order terms in Taylor expansion for the difference between real flow and the basic equation of MI simulation with respect to uN ‒ DN(u) and pN ‒ DN(p), we can derive the linearized error dynamics:
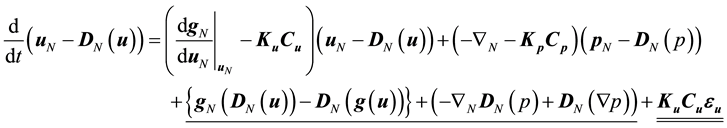 (8)
(8)
and complementary static equation for pressure error:
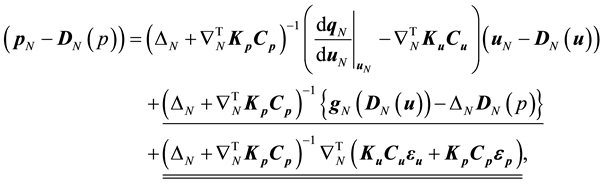 (9)
(9)
where the underlined terms are caused by the model error, including that in the boundary conditions, and the double-underlined terms are caused by measurement error.
Here, we derive the basic equation of eigenvalue analysis for the linearized error dynamics in Equations (8) and (9), considering the case of no model error, including that in the boundary conditions, no measurement error, and feedback with only velocity components (Kp = 0). In this case, Equation (8) is written as
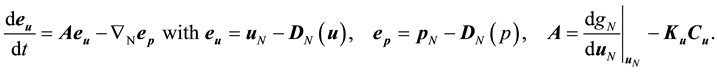 (10)
(10)
Next we reduce the dimension of the velocity error vector eu based on the Weyl decomposition. In Weyl decomposition, any vector field w can be uniquely decomposed into the orthogonal vector fields v and grad ϕ as
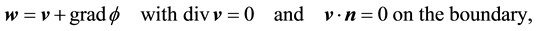 (11)
(11)
where n denotes the unit vector normal to the boundary. In the present analysis, the velocity error eu consists only of v component in Weyl decomposition since it satisfies the divergence-free condition and it vanishes on the boundary due to the above mentioned assumption of no model error. This enables us to reduce the dimension of eu corresponding to that of the component of grad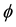 .
.
We define 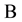 as the range of
as the range of![]() , and 3N-by-2N matrix
, and 3N-by-2N matrix ![]() consisting of
consisting of ![]() the orthonomal basis of
the orthonomal basis of![]() , the orthogonal complementary space of B.
, the orthogonal complementary space of B.
The projection of Equation (10) onto ![]() results in the following relation.
results in the following relation.
![]() (12)
(12)
We can analyze the linearized error dynamics from the eigenvalues of the 2N-by-2N system matrix![]() .
.
Figure 2 shows an example of eigenvalue analysis [21] . Four thousand eigenvalues are shown in a complex plane for the linearized error dynamics of MI simulation for a fully developed turbulent flow with the feedback using two, streamwise and spanwise, velocity components. All the eigenvalues lay in the left half of the complex plane with the negative real part implying convergence of MI simulation to the target turbulent flow. The convergence property obtained in a numerical experiment of MI simulation was in good agreement with that estimated by the eigenvalue analysis [21] .
2.3. Stabilization
This section deals with the destabilization phenomenon of MI simulation [22] . The mechanism of the phenomenon was investigated based on the sufficient condition of the convergence of iterative calculation of the existing MI simulation. A new MI simulation scheme was derived by evaluating the feedback signal in the linear term to remove the cause of the destabilization.
We consider the case in which the time derivative term of Equation (4) is discretized with the first order implicit scheme. In this case, considering Equation (6) with ![]() for simplicity, we obtain the following expression:
for simplicity, we obtain the following expression:
![]() (13)
(13)
where (‒1) of the second component of the subscript of the left-hand side represents the value of the former time step. In the present study, we employ the SIMPLER method [28] as the numerical scheme. Because of the space limitation, the standard way to deal with the pressure equation and the pressure correction equation is omitted.
Since the first term of the right-hand side of Equation (13) is nonlinear with respect to![]() , the term is linearized and the resultant linear equation is repeatedly solved until a convergent solution is obtained. The fundamental equation for the iterative calculation of MI simulation in former studies is written as follows:
, the term is linearized and the resultant linear equation is repeatedly solved until a convergent solution is obtained. The fundamental equation for the iterative calculation of MI simulation in former studies is written as follows:
![]()
Figure 2. Eigenvalue distribution of MI simulations for a turbulent flow in a square duct with feedback of partial velocity components [21] .
![]() (14)
(14)
The above linear equation for ![]() is solved with given
is solved with given![]() , where n in the superscript is the index of iteration. A
, where n in the superscript is the index of iteration. A ![]() is the 3N ´ 3N matrix of linearized coefficients obtained from the nonlinear term
is the 3N ´ 3N matrix of linearized coefficients obtained from the nonlinear term ![]() in
in
Equation (13). It is noted that the feedback signal is included in Γ as the source terms in the formulation of MI simulation of former studies.
Taking the difference between Equation (14) evaluated at iteration number n and that evaluated at n ‒ 1, and applying the mean value theorem, the following relation is obtained:
![]() (15)
(15)
Norms of matrices in the above expression are defined as the induced norms which represent the maximum magnification of linear transformation [29] .
From Equation (15), a sufficient condition of convergence of ![]() as
as ![]() is derived so that the coeffi-
is derived so that the coeffi-
cient in the iteration is less than 1. Substituting the second and third expressions of Equation (14) into this relation, we obtain the following relation:
![]() (16)
(16)
where![]() ,
, ![]() , and
, and ![]() are derivatives of
are derivatives of![]() ,
, ![]() , and
, and ![]() with respect to
with respect to![]() .
.
Assuming that the computational time step Δt is relatively small and that the feedback gain is relatively large, we obtain the sufficient condition of convergence of MI simulation as![]() , and the critical value of the feedback gain matrix norm for the destabilization phenomenon as
, and the critical value of the feedback gain matrix norm for the destabilization phenomenon as
![]() (17)
(17)
This relation agrees with the empirical relation obtained in a former study [25] .
In summary, the destabilization phenomenon of existing MI simulation is ascribed to the fact that a large feedback signal in the source term determines the leading term of the numerator of the coefficient for the successive change in the iterative calculation, and, therefore, divergence occurs with a coefficient larger than 1 or with a feedback gain larger than the critical value.
Patankar [28] formulated four rules which ensure the stable convergence of a finite-volume-based algorithm towards a physically realistic numerical solution. In Rule 3, negative-slope linearization of the source term, he pointed out that an appropriate linearization of the source term is the key to obtaining a convergent solution. The destabilization phenomenon of MI simulation is considered to be the result of an inappropriate treatment of the source term.
According to the above discussion, it is naturally expected that the cause of the destabilization phenomenon can be eliminated by evaluating the feedback signal in the linear term in the iterative calculation. If we move the feedback term relating to ![]() from the source term in the right-hand side to the linear term in the left side of the first expression of Equation (14), we obtain a new iterative calculation scheme as follows:
from the source term in the right-hand side to the linear term in the left side of the first expression of Equation (14), we obtain a new iterative calculation scheme as follows:
![]() (18)
(18)
where modification from the original scheme is underlined. Using the above expressions, we obtain the following relation instead of Equation (16).
![]() (19)
(19)
This relation is satisfied for the feedback gain matrix having only positive or zero eigen values, which is always satisfied for appropriate MI simulation.
Figure 3 shows the critical feedback gains with the computational time step plotted for the results of UMI simulation for blood flow in an aneurismal aorta (Case 1) [25] [30] , magnetic-resonance measurement-inte- grated (MR-MI) blood flow simulation in a cerebral aneurism (Case 2) [26] , and MI simulation for the turbulent flow in a square duct (Case 4). Theoretical values for the critical feedback gain were obtained from Equation (17). The present theoretical result for the critical feedback gain for the convergence of MI simulation is in good agreement with those obtained in the numerical experiment for all the cases treated in the study.
The validity of the stabilized MI simulation scheme is investigated for the case of the turbulent flow in a square duct. Figure 4 shows the variation of the steady error norm with the feedback gain, comparing the stabilized scheme (solid line) and the original scheme (broken line). The critical feedback gain of convergence of MI simulation obtained from the theoretical analysis is also plotted. The error norm with the original scheme suddenly increases in the range of the feedback gain larger than the critical value, but that of the stabilized scheme continuously decreases in this region.
3. Applications
In this section, applications of MI simulation are presented ranging from fundamental turbulent flow in pipes [1] [13] [23] and Karman vortices in a wind tunnel [14] [24] to clinical application of diagnosis of blood flows in the human body [16] [25] -[27] .
3.1. Turbulent Flow in Pipes
Hayase et al. [13] first applied the flow field state observer to analysis of a fully developed turbulent flow in a
![]() Time step Δ t
Time step Δ t
Figure 3. Critical feedback gain with the computational time step compared between theory and numerical experiment [22] .
![]()
Figure 4. Variation of the steady error norm with the feedback gain compared between conventional and stabilized MI simulation schemes for fully developed turbulent flow in a square duct [22] .
square duct showing that the observer, being a fundamental element in the control system theory, is also of potential use in the analysis of flow related problems as an integrated computational method with the aid of experimental measurement. A standard finite volume flow simulation algorithm was modified to the observer by adding a feedback controller, which compensated the boundary condition of the simulation based on the estimation error between output signals of the experimental measurement and the computational result. In that study, the validity of the proposed observer was confirmed by numerical experiment for the turbulent flow through a duct with a square cross section. The physical flow was modeled by a pre-calculated numerical solution of the developed turbulent flow. The estimation error in the stream-wise velocity component at the grid points on the output measurement plane was fed back to the pressure boundary condition based on the simple proportional control law.
![]() (20)
(20)
where Kp is the proportional feedback gain, ![]() and
and ![]() are a modified and an initial pressure difference applied to the grid points upstream and downstream boundary planes of the model flow as the boundary condition, and
are a modified and an initial pressure difference applied to the grid points upstream and downstream boundary planes of the model flow as the boundary condition, and ![]() and
and ![]() are streamwise velocity components at the grid points on a measurement plane at a fixed streamwise coordinate i. Appropriate choice of the feedback gain accelerates the convergence of the result to the standard solution and reduces the final estimation error in the whole domain. The study mainly focused on the case in which the grid system is the same for both the observer and the standard solution. Additional calculation using the standard solution of a finer grid system suggests that more significant improvement of the numerical accuracy can be expected in a realistic case where the standard solution is calculated in a finer grid or replaced by experimental measurement of real flows, as shown in Figure 5.
are streamwise velocity components at the grid points on a measurement plane at a fixed streamwise coordinate i. Appropriate choice of the feedback gain accelerates the convergence of the result to the standard solution and reduces the final estimation error in the whole domain. The study mainly focused on the case in which the grid system is the same for both the observer and the standard solution. Additional calculation using the standard solution of a finer grid system suggests that more significant improvement of the numerical accuracy can be expected in a realistic case where the standard solution is calculated in a finer grid or replaced by experimental measurement of real flows, as shown in Figure 5.
Reproduction of a turbulent flow in a square duct by MI simulation was further investigated by Imagawa et al. [1] . A numerical experiment for the MI simulation was performed with the feedback of velocity vectors of the standard solution for the cases using 1) all velocity components at all grid points, 2) partial velocity components at all grid points, or 3) all velocity components at partial grid points. The result of the MI simulation using all the velocity information exponentially converges to the standard solution with a steady state error reduced from that of the ordinary simulation. For the MI simulation with feedback using limited information, the feedback using two velocity components by omitting one transverse velocity component and the feedback at the grid points skipped in the stream wise direction showed good results (Figure 6).
Nakao et al. [23] investigated MI simulation of steady and unsteady oscillatory airflows passing over an orifice plate in a pipeline. In their study, a turbulent k-ε model was used for a turbulent flow model, and two feedback methods, namely, velocity feedback and pressure feedback, were investigated. As the feedback signal, artificial body force proportional to the difference between the calculated and measured velocity behind the orifice or pressure difference between upstream and downstream edges of the orifice plate was added over the cross section of the measurement point. Figure 7(a) shows the experimental apparatus for the unsteady flow experiments, and Figure 7(b) shows the locations of the velocity and pressure measurement. It was confirmed that the velocity distribution becomes closer to real flow with the velocity feedback and that a global image of the flow field is reproduced with the pressure feedback. Figure 8(a) shows a comparison of the pressure at points P in the experiment and in the simulation. The pressures calculated by MI simulation with pressure feedback can represent the measured pressure. The velocities at point F are compared in Figure 8(b) between the experiment and simulations. Although the k-ε model cannot reproduce the velocity fluctuations, the average velocities were properly calculated by MI simulation with velocity feedback.
3.2. Karman Vortices
Nisugi et al. [14] dealt with a new flow analysis system, namely, the hybrid wind tunnel, which integrates the experimental measurement with a wind tunnel and a numerical simulation with a computer in the framework of the flow field observer (Figure 9). Analysis was performed for the fundamental flow with the Karman vortex street in the wake of a square cylinder. A specific feature of the hybrid wind tunnel is the existence of a feed-
![]()
Figure 5. Convergence of u1-velocity at the center of output measurement plane. Grid (A): 20 ´ 10 ´ 10, Grid (B): 80 ´ 40 ´ 40 [13] .
![]()
![]() (a) (b)
(a) (b)
Figure 6. Steady errors with the feedback gain for MI simulations with the feedback using (a) partial velocity components at all grid points and (b) velocity at partial grid points skipped in the streamwise direction [1] .
![]() (a) (b)
(a) (b)
Figure 7. Unsteady flow experiment: (a) apparatus and (b) measurement points [23] .
![]()
![]() (a) (b)
(a) (b)
Figure 8. Experiment and analysis results: (a) pressures at point P and (b) streamwise velocities at point F [23] .
![]() (a)
(a)![]() (b)
(b)
Figure 9. Hybrid wind tunnel: (a) geometry of the wind tunnel and (b) construction of the flow field observer with definitions of output, feedback signal, and feed-forward signal [14] .
back signal to compensate for the error in the pressure on the side walls of the cylinder and the feed-forward signal to adjust the upstream velocity boundary condition. As compared with the ordinary simulation, the hybrid wind tunnel substantially improves the accuracy and efficiency of the analysis of the flow. Especially, the oscillation of the flow due to the Karman vortex street reproduced with the hybrid wind tunnel exactly synchronizes with that of the experiment. In comparison with the experimental measurement, the hybrid wind tunnel provides more detailed information on the flow than the experiment.
Figure 10 compares the result of the hybrid wind tunnel with that of the experiment. Figure 10(a) shows the differential pressure between the center of the sidewall and that of the front wall (output signal). The waveform of the pressure oscillation with the hybrid wind tunnel agrees well with that of the experiment. Comparison of the velocity u at monitoring point M in Figure 10(b) reveals that the result of the hybrid wind tunnel precisely tracks the velocity variation of the experiment with a laser Doppler velocimetry (LDV) after the transient state.
Figure 11 compares the streak lines at the same instant between the experiment and the hybrid wind tunnel. Streak lines in the experiment represent the typical flow pattern of the Karman vortex street. The hybrid wind tunnel yields a flow pattern very similar to that of the experiment, including the phase of the oscillation.
Yamagata et al. [24] proposed use of MI simulation coupled with particle Image velocimetry (PIV) for a flow with the Karman vortex street behind a square cylinder (Figure 12). The validity of the PIV measurement-inte- grated (PIV-MI) simulation was examined in a numerical experiment. The effect of the feedback data rate was investigated by changing the feedback frequency and the feedback area. As a result, the two-dimensional (2D) PIV-MI simulation with full feedback shows good agreement with the midplane result of the three-dimensional (3D) standard solution for both the mean velocity and the velocity fluctuation. From the viewpoint of the reduced feedback data rate, spatially limited feedback shows better results for reduced feedback data than temporarily limited feedback (Figure 13). The effectiveness of the PIV-MI simulation was experimentally validated, confirming that the information around the cylinder is important for reproduction of the wake behind the cylinder (Figure 14).
![]()
![]() (a) (b)
(a) (b)
Figure 10. Results of the hybrid wind tunnel analysis and the experiment: (a) pressure at A on the cylinder wall and (b) velocity at monitoring point M [14] .
![]()
![]() (a) (b)
(a) (b)
Figure 11. Streak lines (t = 17.9 s): (a) experiment and (b) hybrid wind tunnel [14] .
![]()
![]() (a) (b)
(a) (b)
Figure 13. Mean error in streamwise velocity against feedback data rate: (a) mean velocity and (b) velocity fluctuation [24] .
3.3. Blood Flows
Acquisition of detailed information on the velocity and pressure fields of blood flow is essential for development of an accurate diagnosis or treatment for circulatory diseases. A possible way to obtain such information is integration of numerical simulation and color Doppler ultrasonography in the framework of the flow field observer. Funamoto et al. [16] proposed ultrasonic-measurement-integrated (UMI) simulation (Figure 15). They performed a numerical study on the fundamental characteristics of UMI simulation using a simple two-dimen- sional model problem for blood flow in an aorta with an aneurysm. The result of UMI simulation in the feedback domain converged to the standard solution, even with the usual inevitable incorrect upstream boundary conditions. An example of UMI simulation with feedback from real color Doppler measurement also showed good agreement with measurement (Figure 16).
Ultrasonic-measurement-integrated (UMI) simulation to reproduce three-dimensional steady and unsteady blood flows in an aneurysmal aorta with realistic boundary conditions was investigated [25] [30] . The transient characteristics of the UMI simulation were evaluated by the time constant or equivalently by the frequency response to the oscillating flow, and the steady characteristics were evaluated by the steady state error of the velocity vectors in an aneurysm. Velocity error vectors against the standard solution are shown in Figure 17 [25] . In the initial state, the result is the same as that of the ordinary simulation with large error vectors. The error vectors decrease in and behind the feedback domain due to the effect of the feedback in the UMI simulation and converge to the steady state with small velocity errors.
Recently, Kato et al. [27] have developed an automated two-dimensional UMI (2D-UMI) blood flow analysis system for clinical diagnosis, and have investigated the feasibility of the system for hemodynamic analysis in a carotid artery. The system automatically generates a 2D computational domain based on ultrasound color Doppler imaging and performs a 2D-UMI simulation of blood flow field to visualize hemodynamics in the domain. In the UMI simulation, compensation of errors was applied by adding feedback signals proportional to the differences between Doppler velocities by measurement and computation, while automatically estimating the inflow velocity.
Magnetic resonance (MR)-measurement-integrated (MR-MI) simulation, in which the difference between the computed velocity field and the phase-contrast MRI measurement data is fed back to the numerical simulation,
![]()
Figure 15. Two-dimensional ultrasonic-measurement-integra- ted (2D-UMI) blood flow analysis system.
![]()
![]() (a) (b)
(a) (b)
Figure 16. Color Doppler images in deceleration phase: (a) measurement and (b) UMI simulation [15] .
has been also investigated [26] . The computational accuracy and the fundamental characteristics, such as steady and transient characteristics, of the MR-MI simulation were investigated by a numerical experiment for the three-dimensional steady and unsteady blood flow fields in a cerebral aneurysm developed at a bifurcation (Figure 18).
![]()
![]() (a) (b)
(a) (b)
Figure 17. Velocity error vectors of UMI simulation in (a) initial state and (b) convergent state [25] .
![]()
![]()
![]() (a) (b) (c)
(a) (b) (c)
Figure 18. Streamlines: (a) standard solution, (b) ordinary simulation and (c) MR-MI simulation [26] .
4. Summary
In spite of the inherent difficulty, reproducing the exact structure of complex real flows is a critically important issue in many fields. In order to solve the problem, extensive studies have been carried out on methodology to integrate measurement and simulation. Measurement-integrated (MI) simulation, one of these methods, is a state observer in which a computational fluid dynamics (CFD) scheme is used as a mathematical model of the physical system. A large dimensional nonlinear CFD model makes it possible to accurately reproduce real flows for properly designed feedback signal. This review article surveyed theoretical formulations and applications of MI simulation. Formulations of MI simulation were presented for governing equations of a flow field observer, linearized error dynamics, and stabilization of the numerical scheme. Applications of MI simulation were presented ranging from fundamental turbulent flows in pipes and Karman vortices in a wind tunnel to clinical application to diagnosis of blood flows in a human body.
Acknowledgements
The author acknowledges former Transdisciplinary Fluid Integration Research Center, Advanced Fluid Information Research Center, and Institute of Fluid Science, Tohoku University for their support in establishing integrated research methodologies, including MI simulation.