Asymptotic Behavior of Stochastic Strongly Wave Equation on Unbounded Domains

Zhaojuan Wang^1*, Shengfan Zhou²

¹School of Mathematical Science, Huaiyin Normal University, Huaian, China.
²Department of Mathematics, Zhejiang Normal University, Jinhua, China.

DOI: 10.4236/jamp.2015.33046                

Abstract

We study the asymptotic behavior of solutions to the stochastic strongly damped wave equation with additive noise defined on unbounded domains. We first prove the uniform estimates of solutions, and then establish the existence of a random attractor.

Keywords

Stochastic Strongly Damped Wave Equation, Random Dynamical System, Random Attractor

1. Introduction

Let 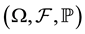be a probability space, where

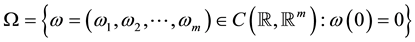
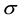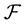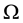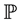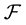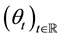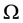the Borel -algebra on is generated by the compact open topology (see [1] ), and is the corresponding Wiener measure on. Define on via

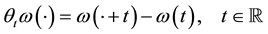
Thus, 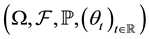is an ergodic metric dynamical system.

Consider the following stochastic strongly damped wave equation with additive noise defined in the entire space :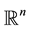

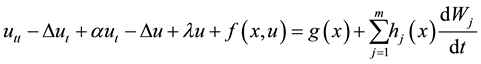(1)

with the initial value conditions

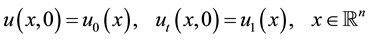(2)

where 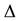is the Laplacian with respect to the variable, is a real function of and; are positive constants, and are given; is a nonlinear

function satisfying certain dissipative and growth conditions, and are independent two-sided real-

valued Wiener processes on. We identify with, i.e.,

Many works have been done regarding the dynamics of a variety of systems related to Equation (1). For example, the asymptotical behavior of solutions for deterministic strongly damped wave equation has been studied by many authors (see [2] -[11] , etc.). For stochastic wave equation, the asymptotical behavior of solutions have been studied by several authors (see [12] -[25] , etc.). However, no results have been presented on random attractors for stochastic strongly damped wave equation (1) with additive noise on unbounded domains to date.

In general, the existence of global random attractor depends on some kind compactness (see, e.g., [26] -[30] ). For Cauchy problem, the main question is how to overcome the difficulty of lacking the compactness of Sobolev embedding in unbounded domains. For some deterministic equations, the difficulty caused by the unboundedness of domains can be overcome by the energy equation approach. The energy equation method was developed by Ball in [31] [32] and used by many authors (see, e.g., [33] -[39] ). Under certain circumstances, the tail-esti- mates method can be used to deal with the problem caused by the unboundedness of domains (see [40] ). In this paper, we will combine the splitting technique in [20] with the idea of uniform estimates on the tails of solutions to investigate the existence of global attractor of the stochastic strongly damped wave Equation (1) defined on unbounded domains. The rest of this paper is organized as follows. In the next section, we recall some basic concepts related to random attractor for general random dynamical systems. In Section 3, we provide some basic settings about Equation (1) and show that it generates a random dynamical system, and then we prove the uniform estimates of solutions and obtain the existence of a random attractor for Equation (1).

Throughout this paper, we use and to denote the norm and the inner product of, respectively. The norm of a Banach space X is generally written as. The symbol is a positive constant which may change its value from line to line.

2. Preliminaries

In this section, we collect some basic knowledge about general random dynamical systems (see [1] [41] for details). Let be a separable Hilbert space with Borel -algebra. Let be the metric dynamical system on the probability space.

In the following, a property holds for -a.e. means that there is with and for.

Definition 1 A continuous random dynamical system on X over is a

-measurable mapping

such that the following properties hold

・ is the identity on;

・ for all;

・ is continuous for all.

Definition 2 (See [41] )

・ A set-valued mapping, , is said to be a random set if the mapping is measurable for any. If is also closed (compact) for each, is called a random closed (compact) set. A random set is said to be bounded if there exist and a random variable such that

・ A random set is called tempered provided for -a.e.,

where.

Let be the set of all random tempered sets in.

・ A random set is said to be a random absorbing set if for any tempered random set, and -a.e., there exists such that

・ A random set is said to be a random attracting set if for any tempered random set, and -a.e., we have

where is the Hausdorff semi-distance given by for any.

・ is said to be asymptotically compact in if for -a.e., has a conver- gent subsequence in whenever, and with.

・ A random compact set is said to be a random attractor if it is a random attracting set and for -a.e. and all.

Theorem 1 (See [41] ) Let be a continuous random dynamical system with state space over. If there is a closed random absorbing set of and is asymptotically com- pact in, then is a random attractor of, where

Moreover, is the unique random attractor of.

3. Existence of Random Attractor

3.1. Basic Settings

In this subsection, we outline some basic settings about (1)-(2) and show that it generates a random dynamical system.

Let where is a small positive constant whose value will be determined later, then (1)-(2) can be rewritten as the equivalent system

(3)

with the initial value conditions

(4)

where,.

Let for and. The function f will be assumed to satisfy the following conditions,

(F1)

(F2)

(F3)

(F4)

where for and for, , , and, are positive constant. Note that (F1) and (F2) imply

(5)

For our purpose, it is convenient to convert the problem (3)-(4) (or (1)-(2)) into a deterministic system with a random parameter, and then show that it generates a random dynamical system.

Let be the ergodic metric dynamical system in Section 1. For, consider the one-dimensional Ornstein-Uhlenbeck equation

Its unique stationary solution is given by

Note that the random variable is tempered, and there is a -invariant with such that is continuous for and. Therefore, it follows from Proposition 4.3.3 in [1] that for any, there exists a tempered function such that

(6)

where satisfies, for -a.e.,

(7)

Then it follows from the above, for -a.e.,

(8)

Put, which solves.

Now, let, we obtain the equivalent system of (3)-(4),

(9)

with the initial value conditions

(10)

where,. We will consider (9)-(10) for and write as from now on.

Let, endowed with the usual norm

(11)

where denotes the usual norm in and stands for the transposition.

By a standard method as in [2] [3] [42] , one may show that under conditions (F1)-(F4), for, problem (9)-(10) has a unique solution which is continuous with respect to in for all. Hence, the solution mapping

(12)

generates a continuous random dynamical system, where. Introducing the homeomorphism, whose inverse homeomorphism

Then, the transformation

(13)

also generates a random dynamical system associated with (3)-(4). Note that the two random dynamical systems are equivalent. By (13), it is easy to check that has a random attractor provided possesses a random attractor. Then, we only need to consider the random dynamical system.

3.2. Uniform Estimates of Solutions

In this subsection, we derive uniform estimates on the solutions of the stochastic strongly damped wave Equations (3)-(4) defined on when. These estimates are necessary for proving the existence of bounded absorbing sets and the asymptotic compactness of the random dynamical system associated with the equations. In particular, we will show that the tails of the solutions for large space variables are uniformly small when time is sufficiently large.

We assume that is the collection of all tempered random subsets of from now on. Let be small enough such that

Set

(14)

where is the positive constant in (F2).

We define a new norm by

(15)

for. It is easy to check that is equivalent to the usual norm in (11).

The next lemma shows that has an absorbing set in.

Lemma 1 Assume that (F1)-(F4), and hold. Then there exists a ran-

dom ball centered at 0 with random radius such that is a random ab-

sorbing set for in, that is, for any and -a.e., there is such that

(16)

Proof. Taking the inner product of the second equation of (9) with in, we find that

(17)

By the first equation of (9), we have

(18)

Then substituting the above into the second and third terms on the left-hand side of (17), we find that

(19)

(20)

From conditions (F1)-(F3) we get

(21)

Using the Cauchy-Schwartz inequality and the Young inequality, we have

(22)

(23)

(24)

By (19)-(24), it follows from (17) that

(25)

Recalling the new norm in (15), by (14) we obtain from (25) that

(26)

Using the Gronwall lemma, we have

(27)

Substituting by, then we have from (27) that

(28)

By (5), we get

(29)

By assumption, is tempered. Then, by (29), if, we have

(30)

Note that and. By (8) with, we obtain

(31)

By (F3), we have that

(32)

Combining (28), (30), (31) and (32), there is a such that for all,

(33)

where Since is tempered, then, and is a random absorbing set for in. So, the proof is completed.

To prove asymptotic compactness of the random dynamical system, we first prove that the solutions were uniformly small outside a bounded domain and then decomposed the solutions in a bounded domain in terms of eigenfunctions of negative Laplacian as in [20] .

Given, denote by and the complement of.

Choose a smooth function, such that for, and

(34)

and there exist constants, such that, for.

Lemma 2 Assume that (F1)-(F4), and hold. Let and

. Then, for every, there exist and, such that the so-

lution of (9)-(10) satisfies for -a.e., , ,

(35)

Proof. We first consider the random Equations (9)-(10). Then taking the inner product of the second equation

of (9) with in, we obtain

(36)

Substituting in (18) into the third, fourth and fifth terms on the left-hand side of (36), we get that

(37)

(38)

By using conditions (F1), (F2) and (F3), we find

(39)

By the Cauchy-Schwartz inequality and the Young inequality, we obtain

(40)

(41)

(42)

Then it follows from (37)-(42) that

(43)

Letting

(44)

then, by (14) we have from (43) that

(45)

By using the Gronwall lemma, we get that

(46)

By replacing by, it then follows from (46) that

(47)

By using (F3), there exists, such that for all,

(48)

In what follows, we estimate the terms on the right-hand side of (47). By (5), and the fact that is tempered, we have that, there exists, such that for all,

(49)

Since, , and, then, there is, such that for, the second term on the right-hand side of (47) satisfies

(50)

Note that is tempered, and. By (8) with

, there is, such that for all, the third term on the right-hand side of (47) satisfies

(51)

Next, we estimate the forth term on the right-hand side of (47). Using (F3), replacing t by s and then by in (27), we have

(52)

it then follows that

(53)

Since and are tempered and, then for any, there exist and, such that for all and, we obtain

(54)

Letting and, then, combining (48), (49), (50), (51) and (54), we have for all and,

(55)

which implies

(56)

Then we complete the proof.

Let with given by (35) and denote by. Fix and set

(57)

Multiplying (9) by and using (57) we find that

(58)

Considering the eigenvalue problem

(59)

The problem has a family of eigenfunctions with the eigenvalues:

such that is an orthonormal basis of. Given n, let and

be the projection operator.

Lemma 3 Assume that (F1)-(F4), and hold. Let and

. Then, for every, there exist, and

, such that the solution j of (9)-(10) satisfies for -a.e., , and,

(60)

Proof. Let, , , , , . Applying to the first equation of (58), we obtain

(61)

Then applying to the second equation of (58) and taking the inner product of the resulting equation with in, we have

(62)

Substituting in (61) into the the third, fourth and fifth terms on the left-hand side of (62), we have

(63)

(64)

(65)

Using conditions (F1) and (F4), we have

(66)

(67)

(68)

it then follows that

(69)

By using the Cauchy-Schwartz inequality and the Young inequality, we have

(70)

(71)

(72)

(73)

From (63)-(73) we can obtain that

(74)

Since there exist and, such that if and, then by (14) and the new norm in (15), we have

(75)

Using the Gronwall lemma, we have

(76)

By substituting by, we can get from (76) that,

(77)

We next estimate each term on the right-hand side of (77). Since and the fact that is tempered, there exist and, such that if and, then

(78)

Since is tempered, and, then, by (8) with

there are and, such that for all and, the second

term on the right-hand side of (77) satisfies

(79)

Next, we estimate the third term on the right-hand side of (77). By (6), (18) and (33),

(80)

which implies that there exists, such that for,

(81)

Let and. Then, it follows from (78), (79) and (81) that, for all, and,

(82)

which completes the proof.

3.3. Random Attractor

In this subsection, we prove the existence of a global random attractor for the random dynamical system generated by (9)-(10).

Theorem 2 Assume that (F1)-(F4), and hold. Let and. Then the random dynamical system generated by (9)-(10) has a unique global random attractor in.

Proof. Notice that the random dynamical system has a random absorbing set in by Lemma 1.

Next, we will prove that the random dynamical system is asymptotically compact in.

Let, , and. Using Lemma 1, we find that

is a bounded in; that is, for -a.e., there exists such that for all,

(83)

By Lemma 2, we have that there are and, such that for every,

(84)

In addition, it follows from Lemma 3 that there exist, and, such that for every,

(85)

Then, by (57) and (83), is a bounded in, which together with (85)

implies that is precompact in. Recalling (57), we find that

is precompact in, which along with (84) and (12) shows that the random

dynamical system is asymptotically compact in.

Then, by Theorem 1, the random dynamical system generated by (9)-(10) has a unique global random attractor in.

4. Remarks

In the present article, we have discussed the existence of a random attractor to the stochastic strongly damped wave equation with additive noise defined on unbounded domains. It is also interesting to consider the the same

problem for stochastic strongly damped wave equation with multiplicative noise. In this case, the

coefficient of the noise term needs to be suitable small, which is different from (1) that with additive white

noise, this is because that the multiplicative noise depends on the state variable, but the additive noise term is independent of. The authors will pursue this line of research

in the future.

Acknowledgments

We thank the editor and the referee for their comments. The authors are supported by National Natural Science Foundation of China (Nos. 11326114, 11401244, 11071165 and 11471290); Natural Science Research Project of Ordinary Universities in Jiangsu Province (No. 14KJB110003); Zhejiang Natural Science Foundation under Grant No. LY14A010012 and Zhejiang Normal University Foundation under Grant No. ZC304014012. This support is greatly appreciated.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Arnold, L. (1998) Random Dynamical Systems. Springer-Verlag, New York and Berlin. http://dx.doi.org/10.1007/978-3-662-12878-7
[2]	Belleri, V. and Pata, V. (2001) Attractors for Semilinear Strongly Damped Wave Equations on . Discrete and Continuous Dynamical Systems, 7, 719-735. http://dx.doi.org/10.3934/dcds.2001.7.719
[3]	Conti, M., Pata, V. and Squassina, M. (2005) Strongly Damped Wave Equations on with Critical Nonlinearities. Communications on Pure and Applied Analysis, 9, 161-176.
[4]	Chen, F., Guo, B. and Wang, P. (1998) Long Time Behavior of Strongly Damped Nonlinear Wave Equations. Journal of Differential Equations, 147, 339-352. http://dx.doi.org/10.1006/jdeq.1998.3447
[5]	Li, H. and Zhou, S. (2008) On Non-Autonomous Strongly Damped Wave Equations with a Uniform Attractor and Some Averaging. Journal of Mathematical Analysis and Applications, 341, 791-802. http://dx.doi.org/10.1016/j.jmaa.2007.10.051
[6]	Temam, R. (1998) Infinite Dimensional Dynamical Systems in Mechanics and Physics. Springer-Verlag, New York.
[7]	Yang, M. and Sun, C. (2009) Attractors for Strongly Damped Wave Equations. Nonlinear Analysis: Real World Applications, 10, 1097-1100. http://dx.doi.org/10.1016/j.nonrwa.2007.12.001
[8]	Yang, M. and Sun, C. (2010) Exponential Attractors for the Strongly Damped Wave Equations. Nonlinear Analysis: Real World Applications, 11, 913-919. http://dx.doi.org/10.1016/j.nonrwa.2009.01.022
[9]	Zhou, S. (1999) Dimension of the Global Attractor for Strongly Damped Nonlinear Wave Equation. Journal of Mathematical Analysis and Applications, 233, 102-115. http://dx.doi.org/10.1006/jmaa.1999.6269
[10]	Zhou, S. and Fan, X. (2002) Kernel Sections for Non-Autonomous Strongly Damped Wave Equations. Journal of Mathematical Analysis and Applications, 275, 850-869. http://dx.doi.org/10.1016/S0022-247X(02)00437-7
[11]	Zhou, S. (2003) Attractors for Strongly Damped Wave Equations with Critical Exponent. Applied Mathematics Letters, 16, 1307-1314. http://dx.doi.org/10.1016/S0893-9659(03)90134-0
[12]	Chow, P. (2002) Stochastic Wave Equation with Polynomial Nonlinearity. Annals of Applied Probability, 12, 361-381. http://dx.doi.org/10.1214/aoap/1015961168
[13]	Fan, X. (2004) Random Attractor for a Damped Sine-Gordon Equation with White Noise. Pacific Journal of Mathematics, 216, 63-76. http://dx.doi.org/10.2140/pjm.2004.216.63
[14]	Fan, X. and Wang, Y. (2007) Fractal Dimensional of Attractors for a Stochastic Wave Equation with Nonlinear Damping and White Noise. Stochastic Analysis and Applications, 25, 381-396. http://dx.doi.org/10.1080/07362990601139602
[15]	Fan, X. (2008) Random Attractors for Damped Stochastic Wave Equations with Multiplicative Noise. International Journal of Mathematics, 19, 421-437. http://dx.doi.org/10.1142/S0129167X08004741
[16]	Fan, X. (2006) Attractors for a Damped Stochastic Wave Equation of Sine-Gordon Type with Sublinear Multiplicative Noise. Stochastic Analysis and Applications, 24, 767-793. http://dx.doi.org/10.1080/07362990600751860
[17]	Jones, R. and Wang, B. (2013) Asymptotic Behavior of a Class of Stochastic Nonlinear Wave Equations with Dispersive and Dissipative Terms. Nonlinear Analysis: Real World Applications, 14, 1308-1322. http://dx.doi.org/10.1016/j.nonrwa.2012.09.019
[18]	Lu, K. and Schmalfuß, B. (2007) Invariant Manifolds for Stochastic Wave Equations. Journal of Differential Equations, 236, 460-492. http://dx.doi.org/10.1016/j.jde.2006.09.024
[19]	Lv, Y. and Wang, W. (2008) Limiting Dynamics for Stochastic Wave Equations. Journal of Differential Equations, 244, 1-23. http://dx.doi.org/10.1016/j.jde.2007.10.009
[20]	Wang, B.X. and Gao, X.L. (2009) Random Attractors for Wave Equations on Unbounded Domains. Discrete and Continuous Dynamical Systems, Special, 800-809.
[21]	Wang, B. (2011) Asymptotic Behavior of Stochastic Wave Equations with Critical Exponents on . Transactions of the American Mathematical Society, 363, 3639-3663. http://dx.doi.org/10.1090/S0002-9947-2011-05247-5
[22]	Wang, Z., Zhou, S. and Gu, A. (2012) Random Attractor of the Stochastic Strongly Damped Wave Equation. Communications in Nonlinear Science and Numerical Simulation, 17, 1649-1658. http://dx.doi.org/10.1016/j.cnsns.2011.09.001
[23]	Wang, Z., Zhou, S. and Gu, A. (2011) Random Attractor for a Stochastic Damped Wave Equation with Multiplicative Noise on Unbounded Domains. Nonlinear Analysis: Real World Applications, 12, 3468-3482. http://dx.doi.org/10.1016/j.nonrwa.2011.06.008
[24]	Yang, M., Duan, J. and Kloeden, P. (2011) Asymptotic Behavior of Solutions for Random Wave Equations with Nonlinear Damping and White Noise. Nonlinear Analysis: Real World Applications, 12, 464-478. http://dx.doi.org/10.1016/j.nonrwa.2010.06.032
[25]	Zhou, S., Yin, F. and Ou Yang, Z. (2005) Random Attractor for Damped Nonlinear Wave Equations with White Noise. The SIAM Journal on Applied Dynamical Systems, 4, 883-903. http://dx.doi.org/10.1137/050623097
[26]	Crauel, H. (2002) Random Probability Measure on Polish Spaces. Taylor & Francis, London.
[27]	Crauel, H., Debussche, A. and Flandoli, F. (1997) Random Attractors. Journal of Dynamics and Differential Equations, 9, 307-341. http://dx.doi.org/10.1007/BF02219225
[28]	Crauel, H. and Flandoli, F. (1994) Attractors for Random Dynamical Systems. Probability Theory and Related Fields, 100, 365-393. http://dx.doi.org/10.1007/BF01193705
[29]	Flandoli, F. and Schmalfuß, B. (1996) Random Attractors for the 3D Stochastic Navier-Stokes Equation with Multiplicative Noise. Stochastics and Stochastic Reports, 59, 21-45. http://dx.doi.org/10.1080/17442509608834083
[30]	Shen, Z., Zhou, S. and Shen, W. (2010) One-Dimensional Random Attractor and Rotation Number of the Stochastic Damped Sine-Gordon Equation. Journal of Differential Equations, 248, 1432-1457. http://dx.doi.org/10.1016/j.jde.2009.10.007
[31]	Ball, J.M. (1997) Continuity Properties and Global Attractors of Generalized Semiflows and the Navier-Stokes Equations. Journal of Nonlinear Science, 7, 475-502. http://dx.doi.org/10.1007/s003329900037
[32]	Ball, J.M. (2004) Global Attractors for Damped Semilinear Wave Equations. Discrete and Continuous Dynamical Systems, 10, 31-52. http://dx.doi.org/10.3934/dcds.2004.10.31
[33]	Ghidaglia, J.M. (1994) A Note on the Strong Convergence towards Attractors for Damped Forced KdV Equations. Journal of Differential Equations, 110, 356-359. http://dx.doi.org/10.1006/jdeq.1994.1071
[34]	Goubet, O. and Rosa, R. (2002) Asymptotic Smoothing and the Global Attractor of a Weakly Damped KdV Equation on the Real Line. Journal of Differential Equations, 185, 25-53. http://dx.doi.org/10.1006/jdeq.2001.4163
[35]	Ju, N. (2000) The H1-Compact Global Attractor for the Solutions to the Navier-Stokes Equations in Two-Dimensional Unbounded Domains. Nonlinearity, 13, 1227-1238. http://dx.doi.org/10.1088/0951-7715/13/4/313
[36]	Moise, I. and Rosa, R. (1997) On the Regularity of the Global Attractor of a Weakly Damped, Forced Korteweg-de Vries Equation. Advances in Differential Equations, 2, 257-296.
[37]	Moise, I., Rosa, R. and Wang, X. (1998) Attractors for Non-Compact Semigroups via Energy Equations. Nonlinearity, 11, 1369-1393. http://dx.doi.org/10.1088/0951-7715/11/5/012
[38]	Rosa, R. (1998) The Global Attractor for the 2D Navier-Stokes Flow on Some Unbounded Domains. Nonlinear Analysis, 32, 71-85. http://dx.doi.org/10.1016/S0362-546X(97)00453-7
[39]	Wang, X. (1995) An Energy Equation for the Weakly Damped Driven Nonlinear Schrodinger Equations and Its Applications. Physica D, 88, 167-175. http://dx.doi.org/10.1016/0167-2789(95)00196-B
[40]	Bates, P.W., Lu, K. and Wang, B. (2009) Random Attractors for Stochastic Reaction-Diffusion Equations on Unbounded Domains. Journal of Differential Equations, 246, 845-869. http://dx.doi.org/10.1016/j.jde.2008.05.017
[41]	Chueshov, I. (2002) Monotone Random Systems Theory and Applications. Springer-Verlag, New York. http://dx.doi.org/10.1007/b83277
[42]	Pazy, A. (1983) Semigroup of Linear Operators and Applications to Partial Differential Equations. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-5561-1