Motion of Nonholonomous Rheonomous Systems in the Lagrangian Formalism ()
1. Introduction
Nonholonomous systems are beyond a doubt more and more considered, mainly in view of the important implementations they exhibit for mechanical models.
From the mathematical point of view, the draft of the equations for such systems commonly matches the introduction of the quasi-velocities and, starting from the Euler-Poincaré equations [1] , several sets of equations have been formulated.
The time-dependent case is probably more disregarded in literature: we direct here our attention especially to rheonomic systems, admitting the holonomic and nonholonomic constraints and the applied forces to depend explicitly on time.
The nonholonomous restrictions are assumed to be linear, so that the equations of motion can be written in the linear space of the admissible displacements of the system, eliminating the Lagrangian multipliers connected to the constraints.
If on the one hand the use of quasi-velocities formally complicates calculations, on the other hand the final form of the system allows computing the equations merely by means of a list of particular matrices, once the Lagrangian function has been written and the quasi-velocities have been chosen.
We pay attention to keep separated the various contributions to the mobility of the system; the customary stationary case can be easily recovered from the general equations we will write.
An energy balance-type equation, which will be proposed in terms of the quasi-velocities, affirms the conservation of the energy in the full stationary case and shows the contributions of the different terms in the rheonomic context.
We will conclude by presenting some applications of the developed system of equations.
Most of the formal notation used onward is explained just below. For a given a list of variables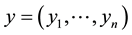 ,
,
the operator 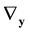 will compute the gradient
will compute the gradient 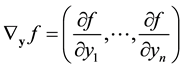 of a scalar funcion
of a scalar funcion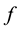 , and
, and 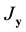 calculates the
calculates the 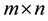 Jacobian matrix of a vector
Jacobian matrix of a vector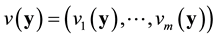 :
: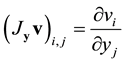 ,
, 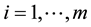 ,
,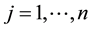 .
.
Anywhere, vectors are in bold type and are meant as columns: row vectors will be written by means of the
transposition symbol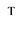 . Moreover,
. Moreover, 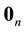 is the null column vector
is the null column vector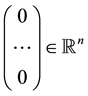 ,
,  is the
is the 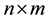 null matrix,
null matrix,
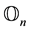 the
the ![]() null matrix and
null matrix and ![]() the unit matrix of size
the unit matrix of size![]() .
.
2. Modelling the System
The theoretical frame we point and expand is contained in [2] .
Let us consider a system of n point particles![]() ,
, ![]() ,
, ![]() restricted both by
restricted both by ![]() geometrical constraints and by
geometrical constraints and by ![]() kinematic constraints,
kinematic constraints, ![]() ,
, ![]() ,
,![]() :
:
![]() (1)
(1)
![]() (2)
(2)
where ![]() is the representative vector of the system and, for each fixed t,
is the representative vector of the system and, for each fixed t, ![]() ,
, ![]() is a matrix of size
is a matrix of size![]() ,
, ![]() a vector in
a vector in![]() . The constraint equations are assumed to be independent:
. The constraint equations are assumed to be independent:
![]() (3)
(3)
We first make use of the ![]() integer relations (1) in order to write the system configuration by means of the parametrisation
integer relations (1) in order to write the system configuration by means of the parametrisation![]() , where
, where![]() ,
, ![]() are the local Lagrangian coordi-
are the local Lagrangian coordi-
nates. The velocity of the system ![]() agrees with (1), but it must be consistent also with the
agrees with (1), but it must be consistent also with the
differential constraints (2) which are rewritten, in terms of the Lagrangian coordinates ![]() and of the generalized velocities
and of the generalized velocities![]() , as
, as
![]() (4)
(4)
and ![]() in case of fixed constraints. The dynamics of the system is summarized in
in case of fixed constraints. The dynamics of the system is summarized in ![]() by
by![]() , where
, where ![]() represents the momentum of the system,
represents the momentum of the system, ![]() ,
, ![]() respectively all active forces and all constraint reactions (the i-th triplet concerning
respectively all active forces and all constraint reactions (the i-th triplet concerning![]() ). The virtual displacements of the system at each time t and at each position
). The virtual displacements of the system at each time t and at each position ![]() are the vectors in
are the vectors in ![]() such that [2]
such that [2]
![]() (5)
(5)
giving in each![]() , t the
, t the ![]() dimensional linear space
dimensional linear space
![]() ,
,
where ![]() are the rows of
are the rows of![]() . At the same time, the assumption of smooth constraints
. At the same time, the assumption of smooth constraints ![]()
![]() make us write
make us write
![]() (6)
(6)
where![]() ,
, ![]() are unknown multipliers.
are unknown multipliers.
The projection of the dynamics equation on the subspace generated by the ![]() vectors
vectors![]() ,
, ![]() (the
(the
columns of![]() ), although such as space strictly includes
), although such as space strictly includes![]() , if
, if![]() , is anyhow noteworthy:
, is anyhow noteworthy:
![]() (7)
(7)
where we assumed ![]() and we defined the Lagrangian function
and we defined the Lagrangian function
![]() (8)
(8)
with ![]() symmetric and positive definite matrix of size
symmetric and positive definite matrix of size ![]() and
and![]() . The
. The ![]() Equation (7) written for the
Equation (7) written for the ![]() unknown quantities
unknown quantities![]() ,
, ![]() have to be considered together with the
have to be considered together with the ![]() Equations (4).
Equations (4).
In order to improve (7), we see from (4) and (5) that ![]() (virtual displacements) is the set of vectors
(virtual displacements) is the set of vectors
![]() such that
such that![]() ,
,![]() .
.
Owing to (3) and recalling (4), it is![]() , hence the solution of the come last linear system, which ex-
, hence the solution of the come last linear system, which ex-
plicitly writes![]() ,
, ![]() is
is
![]() (9)
(9)
with ![]() appropriate coefficients and
appropriate coefficients and ![]() arbitrary factors in
arbitrary factors in![]() ,
,![]() . We conclude that
. We conclude that
![]() , or, equivalently, the
, or, equivalently, the ![]() vectors
vectors![]() ,
, ![]() form a basis for
form a basis for![]() .
.
At this stage, calling ![]() the matrix of size
the matrix of size ![]() and elements
and elements ![]() and noticing that the columns of
and noticing that the columns of ![]() give the basis for
give the basis for![]() , the projection of the dynamics equation on
, the projection of the dynamics equation on ![]() gives, by virtue also of (6):
gives, by virtue also of (6):
![]() (10)
(10)
where the effect of the nonholonomic constraints (through![]() ) on the ordinary Lagrangian equations for hol-
) on the ordinary Lagrangian equations for hol-
onomic systems is evident (in the absence of (2), say![]() , both (10) and (7) are
, both (10) and (7) are![]() ).
).
The ![]() differential Equation (10) are for the
differential Equation (10) are for the ![]() unknown quantities
unknown quantities ![]() and they have to be combined together with the
and they have to be combined together with the ![]() Equation (4). With respect to (7), they have the advantage of not exhibiting the multipliers
Equation (4). With respect to (7), they have the advantage of not exhibiting the multipliers![]() .
.
Remark 2.1 Either Equation (7) or (10) can be employed not necessarily for discrete systems of point particles: once the Lagrangian coordinates have been selected and the Lagrangian function has been written, they can be the same calculated.
The expedience of introducing quasi-velocities (or pseudovelocities) which have to be chosen in a suitable way in order to disentangle the mathematical problem, is by custom performed in nonholonomic systems.
Following the adopted standpoint, the definition of the quasi-velocities steps in establishing a specific (and convenient) connection between ![]() and
and ![]()
![]() (11)
(11)
where ![]() are required to guarantee that the square matrix of size
are required to guarantee that the square matrix of size ![]()
![]() is invertible. In
is invertible. In
this way, each set of kinetic variables ![]() is linked to a singular set of quasi-velocities
is linked to a singular set of quasi-velocities![]() , and vice versa. More precisely, (11) and (4) give
, and vice versa. More precisely, (11) and (4) give
![]() (12)
(12)
where ![]() is the same as (9) and
is the same as (9) and ![]() is a
is a ![]() matrix. The first system in (12) shows both the selection on the coordinates
matrix. The first system in (12) shows both the selection on the coordinates ![]() of the tangent space
of the tangent space ![]() necessary to fulfill the restrictions on the system’s velocity (leading to the subspace
necessary to fulfill the restrictions on the system’s velocity (leading to the subspace![]() ) and the kinematic conditions themselves.
) and the kinematic conditions themselves.
In order to express (10) as a function of the variables![]() ,
, ![]() and to eliminate
and to eliminate![]() , it suffices to extract from (12)
, it suffices to extract from (12)
![]() (13)
(13)
and to define
![]() (14)
(14)
where
![]() (15)
(15)
By using the formulae (see (11))
![]() (16)
(16)
where ![]() is the
is the ![]() matrix whose elements are, for each
matrix whose elements are, for each![]() ,
, ![]()
![]()
we can write (10) in terms of the demanded variables (we use![]() , see (12)):
, see (12)):
![]() (17)
(17)
Remark 2.2 Multiplying both sides of (17) by ![]() and performing the customary steps leading to the energy balance one finds
and performing the customary steps leading to the energy balance one finds
![]() (18)
(18)
In the stationary circumstance![]() ,
, ![]() ,
, ![]() and
and ![]() the Legendre transform
the Legendre transform ![]() of
of ![]() is conserved.
is conserved.
Our next step is writing (17) explicitly, sorting the terms in a suitable way: we start from the calculation
![]() (19)
(19)
so that (17) takes the structure
![]() (20)
(20)
Provided that ![]() means the
means the ![]() -th column of any matrix
-th column of any matrix ![]() and defining for any
and defining for any ![]() the operation
the operation
![]() (21)
(21)
for a matrix ![]() of size
of size![]() , the terms in (20) are defined by the following expressions, where
, the terms in (20) are defined by the following expressions, where ![]() means the
means the ![]() -th component of any vector
-th component of any vector ![]() and
and![]() :
:
![]()
![]()
![]()
Equation (20) is sorted on the strength of the quasi-velocities![]() :
: ![]() is quadratic with respect to
is quadratic with respect to![]() ,
, ![]() is linear with respect to the same variables and
is linear with respect to the same variables and ![]() does not contain
does not contain![]() .
.
Since A is a positive-definite square matrix and![]() , even
, even ![]() is a positive-definite
is a positive-definite ![]()
symmetric matrix. Hence, system (20) + (13) can be written in the normal form![]() , where
, where ![]() is
is
a list of ![]() functions, whose regularity allows us to apply the standard theorems on existence and uniqueness of solutions to first-order equations with given initial conditions.
functions, whose regularity allows us to apply the standard theorems on existence and uniqueness of solutions to first-order equations with given initial conditions.
Before commenting Equation (20), we remark that the ![]() entries of the matrix
entries of the matrix ![]() defined in (21) are, for each
defined in (21) are, for each![]() :
:
![]() (22)
(22)
We see now that a certain number of significant cases are encompassed by (20):
・ merely geometric constraints, corresponding to![]() ,
, ![]() , so that (4) are not present and all the terms containing
, so that (4) are not present and all the terms containing![]() ,
, ![]() and the related quantities
and the related quantities ![]()
![]() must be dropped in (20). Furthermore:
must be dropped in (20). Furthermore:
○ selecting ![]() (quasi-velocities are the generalized velocities) in (11) and (13) means
(quasi-velocities are the generalized velocities) in (11) and (13) means
![]()
so that in (20) are written with as
![]()
thus the Lagrangian equations for geometric constraints (bearing in mind (22))
![]()
![]() , are achieved.
, are achieved.
○ establishing (11) as ![]() (quasi-velocities are the generalized momenta) means
(quasi-velocities are the generalized momenta) means
![]()
In this case (13) together with (20) are the Hamiltonian equations for
![]() :
:
indeed the first one is![]() , whereas (20) reduces to
, whereas (20) reduces to
![]() (23)
(23)
with
![]()
![]()
![]()
(actually from ![]() one deduces
one deduces ![]() and
and ![]() so that, also considering
so that, also considering
![]() , many terms are cancelled).
, many terms are cancelled).
Since ![]() for any
for any![]() , it is
, it is
![]()
therefore (23) is![]() , as stated.
, as stated.
・ Stationary case, where the different contributions producing the dependence on ![]() must be dropped. If one is dealing with a scleronomic system (covering many of common instances), the constraints (1), (2) reduce to
must be dropped. If one is dealing with a scleronomic system (covering many of common instances), the constraints (1), (2) reduce to
![]() (24)
(24)
![]() (25)
(25)
Conditions (24) entail ![]() and
and ![]() (if even the forces are independent of
(if even the forces are independent of
time), on the other hand (25) implies![]() .
.
Equation (11), if one reasonably chooses ![]() and
and ![]() independent of
independent of ![]() (otherwise, changes will be obvious), is
(otherwise, changes will be obvious), is![]() . Since
. Since![]() , system (20) + (13) drastically simplifies to
, system (20) + (13) drastically simplifies to
![]() (26)
(26)
or, index by index, calling ![]() the entries of the matrix
the entries of the matrix![]() ,
, ![]() and having in mind (22)
and having in mind (22)
![]() (27)
(27)
where ![]() is, for each index
is, for each index![]() , the square matrix of order
, the square matrix of order ![]()
![]()
Equations (27) are identified with the Boltzmann-Hamel Equations (17) for the Lagrangian function
![]() (see [3] [4] ). In this case the Legendre transform
(see [3] [4] ). In this case the Legendre transform ![]() is a first integral of
is a first integral of
motion, see Remark 1.2.
・ Reduced Lagrangian function for geometric constraints: in case of ν cyclic variables![]() ,
, ![]() ,
,
(4) can play the role of the ![]() relations derived from the first integral of motion
relations derived from the first integral of motion![]() ,
, ![]() ,
,
that is![]() ,
,![]() . Assuming that
. Assuming that![]() ,
, ![]() , it is possible
, it is possible
to acquire, according to (13), ![]() ,
, ![]() , where
, where![]() ,
, ![]() and bj depend
and bj depend
only on![]() . At this point, setting
. At this point, setting![]() ,
, ![]() ,
, ![]() we have, with respect to (11) and (12),
we have, with respect to (11) and (12), ![]() and
and ![]() (Kronecker’s delta),
(Kronecker’s delta),![]() . Equation (20), which writes simply
. Equation (20), which writes simply
![]() , are the equations of motion for the reduced Lagrangian
, are the equations of motion for the reduced Lagrangian
![]() ,
,
with![]() ,
,![]() ; on the other hand,
; on the other hand, ![]() for
for
![]() , are the so called reconstruction equations.
, are the so called reconstruction equations.
3. Some Applications
We adopt now Equation (20) in order to formulate a couple of remarkable mechanical systems, each of them in a double form, as scleronomous and rheonomous model.
3.1. Pendulum on a Skate
Consider a system of four points![]() ,
, ![]() and
and ![]() equidistant and lying on a horizontal plane,
equidistant and lying on a horizontal plane, ![]() equidistant from
equidistant from ![]() and
and![]() ,
, ![]() oscillating around
oscillating around![]() , equidistant from
, equidistant from ![]() and
and ![]() and coplanar to the latter points and
and coplanar to the latter points and ![]() (see Figure 1).
(see Figure 1).
The system represents a simple model for the motion of a bicycle, as exhibited in [5] : the mass in ![]() is added on order to sketch the rigid structure of the bicycle (just as
is added on order to sketch the rigid structure of the bicycle (just as ![]() and
and ![]() represent the front and the back wheels), as well as the pendulum
represent the front and the back wheels), as well as the pendulum ![]() simulates the movement of a driver.
simulates the movement of a driver.
Let ![]() be a fixed point on the horizontal plane containing
be a fixed point on the horizontal plane containing ![]() and
and![]() ,
, ![]() the ascending vertical versor,
the ascending vertical versor, ![]() the midpoint of the segment
the midpoint of the segment ![]() and
and ![]() perpendicular to the same segment: the geometrical constraints (1) are written by means of the constant assigned values
perpendicular to the same segment: the geometrical constraints (1) are written by means of the constant assigned values![]() ,
, ![]() ,
, ![]() as
as
![]() (28)
(28)
Since the constraints are independent and![]() , we have
, we have![]() ,
,![]() . Setting a fixed reference system
. Setting a fixed reference system ![]() and the angle
and the angle ![]() between
between ![]() and
and![]() , the angle
, the angle ![]() between
between ![]() and
and![]() , the angle
, the angle ![]() between
between ![]() and
and![]() , one defines the orthonormal versors
, one defines the orthonormal versors
![]() , ,
, ,
so that![]() ,
, ![]() ,
, ![]() ,
, ![]() and choose the five parameters
and choose the five parameters ![]() as Lagrangian coordinates, where
as Lagrangian coordinates, where![]() .
.
Opting for considering the segment ![]() as a rigid bar of mass M (instead of a discrete point system, although not significant), the Lagrangian function (8) is written with
as a rigid bar of mass M (instead of a discrete point system, although not significant), the Lagrangian function (8) is written with![]() ,
, ![]() ,
, ![]() and
and
![]()
Figure 1. A simple model for the motion of a bicycle.
![]()
where ![]() is the total mass and
is the total mass and
![]() (29)
(29)
The only one kinetic constraint concerns with the velocity of the back “wheel”![]() , to be aligned with the segment:
, to be aligned with the segment:
![]() (30)
(30)
or![]() , that is (4) for
, that is (4) for![]() ,
, ![]() ,
,![]() .
.
Hence ![]() and the four quasi-velocities (11) are selected by setting
and the four quasi-velocities (11) are selected by setting
![]() and.
and.
Furthermore, (12) gives
![]()
so that
![]()
By computing the first line in (26) one finds the four equations of motion
![]()
joined with the conservation of the quantity![]() .
.
3.2. Assignment of the Front Motion
We modify the previous model by forcing the velocity of the front “wheel” to be a known function of time (a simpler version was considered in [6] for the motion of a bike):![]() . With respect to (28), time
. With respect to (28), time ![]() enters explicitly the geometrical constraints and the fourth one has to be removed. Hence, in this example we have
enters explicitly the geometrical constraints and the fourth one has to be removed. Hence, in this example we have![]() ,
, ![]() ,
, ![]() and we choose
and we choose![]() . The midpoint
. The midpoint ![]() is located by
is located by ![]() and the Lagrangian function (8) is written with
and the Lagrangian function (8) is written with
![]() , ,
, ,
whereas ![]() is the same function.
is the same function.
The constraint (30) is now![]() , that is (4) for
, that is (4) for![]() ,
,![]()
![]() . Choosing
. Choosing![]() ,
, ![]() we have simply
we have simply
![]()
Equation (20) are written with
![]()
and correspond to
![]()
The energy balance (18) writes ![]() and the function in the right side of the latter equality is
and the function in the right side of the latter equality is
![]()
with![]() .
.
3.3. Rolling Disk with Pendulum
A different version of the model 3.1 lies in replacing the bar with a disk and obtaining the unicycle with rider model presented in [7] (see Figure 1 again, replacing the bar with the disk). The system we consider here is a disk of diameter ![]() and mass
and mass![]() , in addition to the same points
, in addition to the same points ![]() (with mass
(with mass![]() ) and
) and ![]() (with mass
(with mass![]() ). We directly choose the coordinates (see Remark 2.1)
). We directly choose the coordinates (see Remark 2.1) ![]() where the new parameter
where the new parameter ![]() is the angle of rotation of the disk around the axis perpendicular to the disk and passing through the centre. The Lagrangian function is written with
is the angle of rotation of the disk around the axis perpendicular to the disk and passing through the centre. The Lagrangian function is written with ![]() and
and
![]()
where ![]() and (see (29))
and (see (29))
![]()
The kinematic constraint of rolling without sliding entails the zero velocity of the contact point![]() :
:
![]() (31)
(31)
which is (4) with![]() ,
, ![]() and
and![]() .
.
This time ![]() and the choice
and the choice
![]()
leads to
![]()
where![]() . Moreover
. Moreover
![]()
with
![]()
and the corresponding equations of motion (20) are
![]()
where
![]()
3.4. Assigned Rotational Velocity of the Disk
We finally consider the same system with the differential constraint (31), but ![]() assigned (we may think about an engine-driven motor bike or electric bike): in that case
assigned (we may think about an engine-driven motor bike or electric bike): in that case ![]() and (4) is setted
and (4) is setted
with ![]() and
and![]() ,
,![]() .
.
The Lagrangian fucntion (8) is written with A the same as in the previous Example 3.1, except for removing
the fourth row and the fourth column, and![]() ,
,![]() . In the matter of (11), which has to be written for
. In the matter of (11), which has to be written for![]() , if one defines the quasi-velocities
, if one defines the quasi-velocities![]() ,
,
![]() ,
, ![]() one gets
one gets ![]() and
and
![]()
Calculating the products in (15) gives
![]() ,
,
![]() ,
,
![]()
and the computation of (20) gives the three equations of motion
![]()
4. Conclusions
The paper aims at formulating a general scheme of equations for rheonomic mechanical systems exposed to either geometrical (1) and differential (2) constraints. We pay special attention to tell apart the different contributions due to the explicit dependence on time, deriving from the holonomous constrictions (via ![]() and
and ![]() of (8)), the nonholonomous constrictions (via
of (8)), the nonholonomous constrictions (via ![]() of (4)) and the definition of quasi-velocities (via
of (4)) and the definition of quasi-velocities (via![]() ) of (11)).
) of (11)).
Since the equations of motion are projected in the subspace of the velocities allowed by the constraints (both holonomous and nonholonomous), the Lagrange multipliers are absent from the equations.
The procedure proposed by (20) requires only calculation of the Jacobian matrix of vectors and the algebraic multiplication of matrices and vectors.
Making use of quasi-velocities renders the equations versatile to more than one formalism and, as it is known, the appropriate choice of them meets the target of facilitating the mathematical resolution of the problem.
The last point is part of the matters listed below and which will be dealt with in the future:
-Find an appropriate choice of the quasi-velocities in order to disentangle (20) from (13) as much as possible,
-Make use of the structure of the equations and of the properties of the various matrices involved in order to study the stability of the system,
-Take advantage of some peculiarity of the system in order to refine the set of equations and achieve information.
The latter subject is faced in [8] [9] for the stationary case by means of a robust and complex theory in connection with symmetries in nonholonomic systems.