1. Introduction
Assessment of blast performance is essential in order to ensure that the extent of objectives of blasts is achieved. There are various methods of blast performance analysis methods using fragmentation analysis and ground vibrations data generated during blasting operations. [1] -[3] have used different methods of fragmentation analysis methods using different initiation systems to assess blast performance; they [4] [5] have used ground vibration data to assess blast performance. Their study focused on estimation of energy wasted in the form of ground vibrations by analyzing ground vibration wave forms.
Theoretically the highest amount of energy is equivalent to detonation energy. Effective comparison of energy of different explosives is done based on weight strength. Only a fraction of energy does useful work in rock blasting and the remaining is wasted in producing detrimental effects like ground vibrations, fly rock, back break, etc. Generally blast performance is analyzed in terms of fragmentation and ground vibration, but these results cannot be expressed directly in terms of their energy content. The reason for this may be that, it is not the energy consumption in different phenomena that matter, but rather the end effects of blasting like degree of fragmentation, throw and vibration levels. Data and estimations on energy components in rock blasting are thus limited to a few researchers. [6] -[8] estimated the amount of energy transformed in kinetic energy of the rock, fracture generation and seismic waves.
Attempts were made by some researchers to measure the explosive energy in laboratory scale using cylinder expansion test. In this test, copper tubes filled with explosives were shot, and the explosive velocity of detonation (VOD) and the expansion velocity of the tube wall were measured. Sum of the kinetic energy of the copper tube and the radial kinetic energy of the gases is called Gurney energy (Ec). Ec is the measure of the work capacity of the explosive [8] .
Energy released by an explosive can be grouped into gaseous energy and shock energy, working on the surrounding strata resulting in fragmenting the medium through various breakage mechanisms. Some of these mechanisms are responsible for (a) fracturing energy that ultimately is responsible for creating new surfaces in the rock fragments; (b) energy transferred as shock waves into the rock mass propagating as seismic waves or ground vibrations beyond the fragmentation zone; and (c) energy to displace the fragmented material and form the muck pile that appears as kinetic energy. This energy partitioning is related to the characteristics of explosives and the strata, and to some extent to the blast geometry. The energy balance of the blast can thus be expressed as [7] .
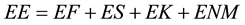 (1)
(1)
where,
EE = explosive energy,
EF = fragmentation energy,
ES = seismic energy,
EK = kinetic energy,
ENM = energy forms not measured.
Seismic Energy
The energy transferred to the rock in the form of seismic waves is calculated as the integral of the energy flow past a control surface at a given distance from the blast. The energy flux (the power or rate of work, per unit area) is the scalar product of the stress at the surface and the particle velocity [9] . Calculations of seismic energy and its comparison with explosive energy have been reported by [10] -[14] and more recently by [15] . [6] attempted to use some of the energy concepts in principles of blast design.
Energy passing through rock mass in the form of seismic waves is seismic energy. [16] suggested the following formula to estimate the seismic energy.
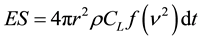 (2)
(2)
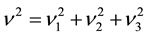
where,
ES = seismic energy (MJ),
r = distance (m),
ρ = rock density (gm/cc),
CL = longitudinal wave velocity (m/s),
ν = magnitude of the vector sum of the velocities (m/s),
ν1 = measured velocity in longitudinal direction,
ν2 = measured velocity in transverse direction,
ν3 = measured velocity vertical direction.
The authors have proposed another concept in estimating energy by analyzing the complete wave forms obtained from ground vibration monitoring. Once the explosive is initiated in the blast hole, energy dissipates into the rock mass, generating strain waves. The intensity of the waves is captured at a point from a known distance from blast site with ground vibration monitor. The geophone captures the wave forms in three mutually orthogonal directions namely, longitudinal, transverse and vertical directions for a fixed duration. There seems to be a relationship between the explosive energy dissipation and the nature of the wave forms. In general the area within the curve of force-displacement diagram is a work done; the same principle is applied for wave forms generated from blast vibrations (Figure 1). As the wave form consists of velocity vs time, no unit is given in terms of energy. Only the quantitative values are used for analysis. Some more research work is going on in this aspect.
In case of a regular curve of equal wave length, the square of the amplitude can be integrated to get the area of the curve. However, wave forms produced from blasting operations are complex and there is a wide variation in wave length. Wave forms, therefore, are analyzed with the help of a signal processing software DaDiSP. Summation of energy in all three directions is taken for estimating the total wave energy from each event.
2. Case Study
A case study was taken up in a civil engineering project site where hard rock is being excavated for construction of a station for an underground metro rail. The hard granitic formation is exposed almost to the surface. Total depth of excavation required is around 20 to 24 m. So, it was planned to remove the rock by benching method using drilling and blasting technique. The area of excavation is surrounded by important buildings. Figure 2 show the drilling process at the site. After drilling, each blast hole is charged with cart ridged explosives and shock tube initiation system is used to initiate each blast hole (Figure 3). As numbers of important buildings are there in the surroundings and therefore, fly rock is a major concern. Muffling was done using rubber blast mats (Figure 4). Each blast was monitored using Minimate, Instantel, Canada, for ground vibrations generation at specific distances (Figure 5).
In total 31 blasts were considered for analysis purpose. Details of blasts like maximum charge per delay, monitoring distance, peak particle velocity, depth of excavation from surface etc., are given in Table 1. Regression analysis was performed between peak particle velocity and scaled distance and the regression coefficient was found to be 0.81, which indicates that the data has a very good correlation (Figure 6).
Seismic energy was estimated as per Equation (2) using the peak particle velocities in longitudinal, vertical and transverse directions, the details of which are given in Table 2. Figure 7 shows the correlation between seismic energy and scaled distance, with a correlation coefficient of 0.79 indicating a very good correlation.
The ground vibration event signals were analyzed using DaDiSP software. Area of each signal in each direction was determined and the total wave energy was estimated by summing up the energy in longitudinal, vertical and transverse directions (Table 2). Figure 8 show the plot between total wave energy and the scaled distance. The wave energy from each blast was compared with the estimated seismic energy. Though it has a poor regres-
![]()
Figure 1. Analysis of ground vibration wave forms using signal processing software.
![]()
Figure 2. A view of drilling operation at excavation site.
![]()
Figure 4. Muffling arrangement on blast area.
![]()
Figure 6. Peak particle velocity vs scaled distance.
![]()
Figure 7. Seismic energy vs scaled distance.
![]()
Table 1. Details of blasts conducted.
PPV: Peak particle velocity, MCD: Maximum charge per delay, SD: Scaled distance.
sion co-efferent, it has similar trend to the previous curves, which can be also an indicator of blast performance.
Figure 9 show the comparison of seismic energy and wave energy at different scaled distances and at a constant depth of excavation of 15 m from surface. At all the scaled distances, the seismic energy and the wave energy shows similar trends. At a lower scaled distance (26.63), the seismic energy and wave energy were high
![]()
Table 2. Work done and seismic energy of different blasts.
SD: Scaled distance, ES: Seismic energy.
compared to higher scaled distance.
Similar to the above, two more sets of data were taken up at 17 m and 19 m depth of excavation from surface (Figure 10 & Figure 11). Similar trend was found as previous case. This shows that at a constant depth of excavation as the scaled distance increases the seismic energy and the wave energy decreases. This is due to the fact that a higher scaled distance indicates either lesser maximum charge per delay or increased distance from
![]()
Figure 8. Wave energy vs scaled distance.
![]()
Figure 9. Seismic energy and work done at different scaled distance and at a constant depth of 15 m.
![]()
Figure 10. Seismic energy and work done at different scaled distance and at a constant depth of 17 m.
o monitoring point.
Figure 12 shows the comparison between seismic energy and total wave energy at different depths of excavation and at a constant scaled distance of 58. As the depth increases, seismic energy and wave energy also in
![]()
Figure 11. Seismic energy and work done at different scaled distance and at a constant depth of 19 m.
![]()
Figure 12. Seismic energy and work done at different scaled distance and at a constant depth of 58 m.
creased. Similar analysis was carried out at a scaled distances of 50 and 69, and similar trend was observed in the results (Figure 13 & Figure 14). This is due to that as the depth increases the rock formation was found to be harder in the field. Through hard rock formation the wave propagation is more active so it resulted in higher seismic energy and higher wave energy as the depth increases. Another reason is that the horizontal monitoring distance is between 22 and 45 m and depth of excavation is between 12 to 25 m. So, at shallow depths of excavation, the seismic wave reaches the surface much before the monitoring point which has led to a lower PPV recording by geophone, where as in case of deeper excavation point, as the seismic wave reaches the surface very near to the geophone and a higher PPV was recorded. So, deeper excavation resulted in higher seismic energy and wave energy though the scaled distance and other parameters were same.
3. Conclusions
The analysis carried out in the chosen construction site has indicated the following useful inferences.
1) The seismic energy dissipated into the rock mass is having good correlation with scaled distance and seismic energy.
2) The work done determined based on three mutually orthogonal directions of ground vibration events is having good correlation with the seismic energy, which is estimated, based on PPV and rock properties.
3) The seismic energy dissipated into the rock mass and the work done by the explosive energy are found to decrease with increase in scaled distance at a given depth of excavation.
4) At a constant scaled distance, as the depth of excavation increases the seismic energy, the work done also increases.
5) Analysis of wave forms using signal processing software is found to be quite useful in analyzing the blast results.
![]()
Figure 13. Seismic energy and work done at different scaled distance and at a constant depth of 50 m.
![]()
Figure 14. Seismic energy and work done at different scaled distance and at a constant depth of 69 m.
6) The work done and seismic energy estimation analogy can be extended further to correlate with fragmentation energy.
NOTES
*Corresponding author.