1. Introduction
Heavy ion collisions at ultra relativistic energies might produce a new form of QCD matter characterized by the deconfined state of quarks and gluons (partons) [1] . Measurements of the production of identified particles provide information about the dynamics of this dense matter. The yield of identified hadrons, their multiplicity distributions, as well as the rapidity and transverse momentum spectra are the basic observables in proton-proton and heavy ion collisions at any energy regime, from a few GeV per nucleon to the new ultra-relativistic LHC regime, spanning c.m. energies of a few TeV [2] . Recently, the different experimental groups in the CERN Large Hadron Collider (LHC) have reported various results for different observables in 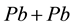 collisions at energy
collisions at energy 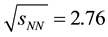 TeV. These results might provide another opportunity to investigate the bulk properties of exotic QCD matter, the so-called QGP-hypothesis. But the exact nature of QGP-hadron phase transition is still plagued by uncertainties [3] .
TeV. These results might provide another opportunity to investigate the bulk properties of exotic QCD matter, the so-called QGP-hypothesis. But the exact nature of QGP-hadron phase transition is still plagued by uncertainties [3] .
Our objective in this work is to use a model, known as “Sequential Chain Model (SCM)”, which is different from “standard” framework, in interpreting the transverse momenta spectra, some ratio-behaviours, rapidity spectra and the nuclear modification factor of the pions, kaons and antiprotons produced in 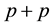 and
and 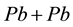 collisions at LHC energy
collisions at LHC energy 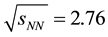 TeV. Very recently, some questions have been arose about the quark constituents of the nucleons. Little of the proton spin is carried by the quarks [4] . So, in order to explain the huge amount of heavy ion collision data, we put forward this model which has no QGP-tag and is different from the quark-hypothesis.
TeV. Very recently, some questions have been arose about the quark constituents of the nucleons. Little of the proton spin is carried by the quarks [4] . So, in order to explain the huge amount of heavy ion collision data, we put forward this model which has no QGP-tag and is different from the quark-hypothesis.
The organization of this work is as follows. In Section 2, we give a brief outline of our approach, the SCM. In the next section (Section 3), the results have been presented with table and figures. And in the last section (Section 4), we offer the final remarks and conclusions.
2. Outline of the Model
This section is divided by two subsections 1) the basic model in 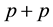 collision and 2) subsequent trans- formation to the
collision and 2) subsequent trans- formation to the  collisions.
collisions.
2.1. The Basic Model: An Outline
According to this Sequential Chain Model (SCM), high energy hadronic interactions boil down, essentially, to the pion-pion interactions; as the protons are conceived in this model as , where
, where 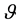 is a spectator particle needed for the dynamical generation of quantum numbers of the nucleons [5] - [11] .
is a spectator particle needed for the dynamical generation of quantum numbers of the nucleons [5] - [11] .
The inclusive cross-section of the ![]() -meson produced in the
-meson produced in the ![]() collisions at high energies has been calculated by using field theoretical calculations and Feynman diagram techniques with the infinite momentum frame approximation method. The inclusive cross-section is given by the undernoted relation [5] - [11]
collisions at high energies has been calculated by using field theoretical calculations and Feynman diagram techniques with the infinite momentum frame approximation method. The inclusive cross-section is given by the undernoted relation [5] - [11]
![]() (1)
(1)
with
![]() (2)
(2)
where ![]() is the normalisation factor which will increase as the inelastic cross-section increases and it is different for different energy and for various collisions. The terms
is the normalisation factor which will increase as the inelastic cross-section increases and it is different for different energy and for various collisions. The terms![]() ,
, ![]() ,
,
![]() in Equation (1) represent the transverse momentum, Feynman Scaling variable respectively. The
in Equation (1) represent the transverse momentum, Feynman Scaling variable respectively. The ![]() in Equation (2) is the square of the c.m. energy.
in Equation (2) is the square of the c.m. energy.
![]() of the expression (1) is the “constituent rearrangement term”. It arises out of the partons inside the proton. At high energy interaction processes the partons undergo some dissipation losses due to impact and impulses of the projectile on the target. This term essentially provides a damping term in terms of a power law. The exponent of
of the expression (1) is the “constituent rearrangement term”. It arises out of the partons inside the proton. At high energy interaction processes the partons undergo some dissipation losses due to impact and impulses of the projectile on the target. This term essentially provides a damping term in terms of a power law. The exponent of![]() , i.e.
, i.e.![]() , varies on both the collision process and the specific
, varies on both the collision process and the specific ![]() -range. We have to parametrize this term with the view of two physical points, viz., the amount of momentum transfer and the contributions from a phase factor arising out of the rearrangement of the constituent partons. The relation for
-range. We have to parametrize this term with the view of two physical points, viz., the amount of momentum transfer and the contributions from a phase factor arising out of the rearrangement of the constituent partons. The relation for ![]() is to be given by [12]
is to be given by [12]
![]() (3)
(3)
where ![]() denotes the average number of participating nucleons and
denotes the average number of participating nucleons and ![]() values are to be obtained phenomenologically from the fits to the data-points.
values are to be obtained phenomenologically from the fits to the data-points.
Similarly, for kaons of any specific variety (![]() ,
, ![]() ,
, ![]() or
or![]() ) we have
) we have
![]() (4)
(4)
with
![]() (5)
(5)
And for the antiproton production in ![]() collision at high energies, the derived expression for inclusive cross-section is
collision at high energies, the derived expression for inclusive cross-section is
![]() (6)
(6)
with
![]() (7)
(7)
2.2. The Path from pp to AB Collisions
In order to transform the inclusive cross-section from ![]() to
to ![]() collisions (here,
collisions (here, ![]() stands for
stands for![]() ,
, ![]() and
and![]() , as the case may be), we use the undernoted relation [13] ;
, as the case may be), we use the undernoted relation [13] ;
![]() (8)
(8)
Here, in the above equation [Equation (8)], the first factor gives a measure of the number of wounded nucle- ons i.e. of the probable number of participants, wherein ![]() gives the probability cross-section of collision with “B” nucleus (target), had all the nucleons of A suffered collisions with B-target. And
gives the probability cross-section of collision with “B” nucleus (target), had all the nucleons of A suffered collisions with B-target. And ![]() has just the same physical meaning, with A and B replaced. Furthermore,
has just the same physical meaning, with A and B replaced. Furthermore, ![]() is the nucleon (proton)-nucleus (A) inter- action cross-section,
is the nucleon (proton)-nucleus (A) inter- action cross-section, ![]() is the inelastic nucleon (proton)-nucleus (B) reaction cross-section and
is the inelastic nucleon (proton)-nucleus (B) reaction cross-section and ![]() is the inelastic AB cross-section for the collision of nucleus A and nucleus B. The values of
is the inelastic AB cross-section for the collision of nucleus A and nucleus B. The values of![]() ,
, ![]() ,
, ![]() have been worked here out by the following formula [14]
have been worked here out by the following formula [14]
![]() (9)
(9)
with ![]() mb,
mb,![]() .
.
The second term in expression (8) is a physical factor related with energy degradation of the secondaries due to multiple collision effects. The parameter ![]() occurring in this term is a measure of the fraction of the nucleons that suffer energy loss. The maximum value of
occurring in this term is a measure of the fraction of the nucleons that suffer energy loss. The maximum value of ![]() is unity, while all the nucleons suffer energy loss. This
is unity, while all the nucleons suffer energy loss. This ![]() parameter is usually to be chosen [13] , depending on the centrality of the collisions and the nature of the secondaries.
parameter is usually to be chosen [13] , depending on the centrality of the collisions and the nature of the secondaries.
3. The Results
This section will be divided in the following sub-sections: i) the ![]() -spectra of pion, kaon and antiproton in both
-spectra of pion, kaon and antiproton in both ![]() and
and ![]() collisions at
collisions at ![]() TeV; ii)
TeV; ii) ![]() and
and ![]() ratio behaviour at
ratio behaviour at ![]() collisions at
collisions at ![]() TeV; iii) rapidity distribution of pion for the most central collisions of
TeV; iii) rapidity distribution of pion for the most central collisions of ![]() in the above-mentioned energy and iv) the nuclear modification factor
in the above-mentioned energy and iv) the nuclear modification factor ![]() in the same energy range.
in the same energy range.
3.1. Transverse Momenta Spectra of Charged Hadron in ![]() and
and ![]() Collision at
Collision at ![]() = 2.76 TeV
= 2.76 TeV
We can write from expression (8), the transformed SCM-based transverse-momentum distributions for ![]() -type reactions in the following generalized notation:
-type reactions in the following generalized notation:
![]() (10)
(10)
where, for example, the parameter ![]() can be written in the following form:
can be written in the following form:
![]() (11)
(11)
In a similar way, the values of ![]() of Equation (10) have been calculated with the help of Equation (1), Equation (2). The values of
of Equation (10) have been calculated with the help of Equation (1), Equation (2). The values of![]() ,
, ![]() ,
, ![]() and
and ![]() have been calculated accordingly by using Equations (4)-(8). Moreover, for calculation for transverse momenta distribution of antiproton production, the the exponential part will be
have been calculated accordingly by using Equations (4)-(8). Moreover, for calculation for transverse momenta distribution of antiproton production, the the exponential part will be ![]()
![]() .
.
![]() of the expression (10) have been calculated by using Equation (3).
of the expression (10) have been calculated by using Equation (3).
3.1.1. Production of![]() ,
, ![]() and
and ![]() in
in ![]() Collision at
Collision at ![]() = 2.76 TeV
= 2.76 TeV
In Table 1, the calculated values of![]() ,
, ![]() and
and ![]() of Equation (10) for
of Equation (10) for![]() ,
, ![]() and
and ![]() produced in proton-proton collisions at
produced in proton-proton collisions at ![]() TeV have been given.
TeV have been given.
In Figure 1, we have drawn the invariant yields against ![]() for
for![]() ,
, ![]() and
and![]() . By using Equation (10) and Table 1 we have plotted the solid lines against the experimental background [15] . The dotted lines in the figure show PYTHIA-based results [15] .
. By using Equation (10) and Table 1 we have plotted the solid lines against the experimental background [15] . The dotted lines in the figure show PYTHIA-based results [15] .
3.1.2. Invariant Yields of![]() ,
, ![]() and
and ![]() in
in ![]() Collision at
Collision at ![]() = 2.76 TeV
= 2.76 TeV
In a similar fashion, the invariant yields of![]() ,
, ![]() and
and ![]() in
in ![]() collision at LHC energy
collision at LHC energy
![]() TeV for different centralities have been plotted in Figures 2(a)-(c) respectively. The solid lines in the figure are the theoretical SCM results while the points show the experimental values [16] . The values of
TeV for different centralities have been plotted in Figures 2(a)-(c) respectively. The solid lines in the figure are the theoretical SCM results while the points show the experimental values [16] . The values of![]() ,
, ![]() and
and ![]() of Equation (10) for pion, kaon and antiproton and for different centralities have been given in Table 2.
of Equation (10) for pion, kaon and antiproton and for different centralities have been given in Table 2.
3.2. The K/π and p/π Ratios
The model-based ![]() and
and ![]() ratios as a function of
ratios as a function of ![]() at energies
at energies ![]() TeV have been obtain- ed from the expression (10) and Table 2. Data in Figure 3(a) and Figure 3(b), for different centralities, viz., for 0% - 5%, 20% - 30% and 70% - 80%, are taken from Ref [16] . Lines in the figure show the theoretical plots.
TeV have been obtain- ed from the expression (10) and Table 2. Data in Figure 3(a) and Figure 3(b), for different centralities, viz., for 0% - 5%, 20% - 30% and 70% - 80%, are taken from Ref [16] . Lines in the figure show the theoretical plots.
3.3. The Rapidity Distribution
For the calculation of rapidity distribution, we can make use of the following standard relation [17] ,
![]() (12)
(12)
By using Equation (1), Equation (8), Table 2 and Equation (12), we arrive at the SCM-based rapidity dis- tribution, which is given hereunder;
![]() (13)
(13)
The ![]() of the above equation (Equation (13)) has come from
of the above equation (Equation (13)) has come from ![]() of Equation (11) with
of Equation (11) with![]() .
.
In Figure 4, we have plotted theoretical ![]() versus
versus ![]() with the help of above equation [Equation (13)] against experimental background [18] . The dotted line in this figure shows the Gaussian fit [18] .
with the help of above equation [Equation (13)] against experimental background [18] . The dotted line in this figure shows the Gaussian fit [18] .
3.4. The Nuclear Modification Factor
The nuclear modification factor (NMF) ![]() is defined as ratio of charged particle yield in
is defined as ratio of charged particle yield in ![]() to that in
to that in![]() , scaled by the number of binary nuclear collisions
, scaled by the number of binary nuclear collisions ![]() [19] and is given hereunder
[19] and is given hereunder
![]() (14)
(14)
where ![]() is related with the average nuclei thickness function
is related with the average nuclei thickness function ![]() by the following relation [19]
by the following relation [19]
![]() (15)
(15)
Here, ![]() is the total inelastic cross section of
is the total inelastic cross section of ![]() interactions.
interactions.
The ![]() is related to
is related to ![]() by the following relation [13] :
by the following relation [13] :
![]() (16)
(16)
In the region, ![]() ,
,![]() .
.
The SCM-based results on NMF’s for![]() ,
, ![]() and
and ![]() in central
in central ![]() collisions at energies
collisions at energies
![]() TeV are deduced on the basis of Equation (10), Table 1 and Table 2. The equations in connection with
TeV are deduced on the basis of Equation (10), Table 1 and Table 2. The equations in connection with![]() ,
, ![]() and
and ![]() are give by the following relations and they are plotted in Figure 5 against
are give by the following relations and they are plotted in Figure 5 against![]() . The solid lines in the figure show the theoretical results, while the points show the experimentally measured results [20] ;
. The solid lines in the figure show the theoretical results, while the points show the experimentally measured results [20] ;
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
4. Discussions and Conclusions
Let us now make some comments on the results arrived at and shown by the diagrams on the case-to-case basis.
1) The invariant yields against transverse momenta ![]() for
for![]() ,
, ![]() and
and ![]() in proton-proton collisions obtained on the basis of the SCM are shown in Figure 1. Except for very low-
in proton-proton collisions obtained on the basis of the SCM are shown in Figure 1. Except for very low-![]() region, there is a bit degree of success. The model disagrees in the low-
region, there is a bit degree of success. The model disagrees in the low-![]() region. This is due to the fact that the model has turned essentially into a mixed one with the inclusion of power law due to the inclusion of partonic rearrangement factor. However, the power-law part of the equation might not be the only factor for this type of discrepancy. The initial condition and dynamical evolution in heavy-ion collisions are more complicated than we expect. Till now, we do not know the exact nature of reaction mechanism. One might take into account some other factors like radial flow or thermal equilibrium.
region. This is due to the fact that the model has turned essentially into a mixed one with the inclusion of power law due to the inclusion of partonic rearrangement factor. However, the power-law part of the equation might not be the only factor for this type of discrepancy. The initial condition and dynamical evolution in heavy-ion collisions are more complicated than we expect. Till now, we do not know the exact nature of reaction mechanism. One might take into account some other factors like radial flow or thermal equilibrium.
2) Similarly, in calculating the yields for different transverse momenta and for different centralities for![]() ,
, ![]() and
and ![]() in lead-lead collisions, we use Equations (8), (9) and (10) along with Equations (1)-(7). The results are given in Table 2 and are depicted in Figures 2(a)-(c) respectively. The top-most curves are for central collisions (0% - 5%) and the lowest curves are peripheral ones (80% - 90%). In between these two curves, other centralities (5% - 10%, 10% - 20%, 20% - 30%, 30% - 40%, 40% - 50%, 50% - 60%, 60% - 70% and 70% - 80%) have been plotted. For the production of pions, the SCM-based results show good fits from central to peripheral collision. Slight disagreements observed at very low-
in lead-lead collisions, we use Equations (8), (9) and (10) along with Equations (1)-(7). The results are given in Table 2 and are depicted in Figures 2(a)-(c) respectively. The top-most curves are for central collisions (0% - 5%) and the lowest curves are peripheral ones (80% - 90%). In between these two curves, other centralities (5% - 10%, 10% - 20%, 20% - 30%, 30% - 40%, 40% - 50%, 50% - 60%, 60% - 70% and 70% - 80%) have been plotted. For the production of pions, the SCM-based results show good fits from central to peripheral collision. Slight disagreements observed at very low-![]() regions for kaons and protons at central collisions. These are due to the power law part of the model. This explanation is also true for low-
regions for kaons and protons at central collisions. These are due to the power law part of the model. This explanation is also true for low-![]() region data in
region data in ![]() collision. Here, we see that the constituent rearrangement terms are clearly centrality dependent.
collision. Here, we see that the constituent rearrangement terms are clearly centrality dependent.
3) The ![]() and
and ![]() ratio behaviours for different centralities are calculated in the light if the SCM and they are plotted in Figure 3(a) and Figure 3(b) respectively. The theoretical
ratio behaviours for different centralities are calculated in the light if the SCM and they are plotted in Figure 3(a) and Figure 3(b) respectively. The theoretical ![]() ratio behaviours are in good agreement with experimental values. Some disagreement are observed in central
ratio behaviours are in good agreement with experimental values. Some disagreement are observed in central ![]() -ratio in low-
-ratio in low-![]() regions.
regions.
4) In explaining the rapidity distribution for production of pions (Figure 4), the majority of the produced secondaries, the model works agreeably with data. The comparison with Gaussian fit is satisfactory.
5) The nuclear modification factors for pion, kaon and proton for central ![]() collisions for different transverse momenta have been calculated and they are plotted in Figure 5. While the theoretical plots are agreeable in low-
collisions for different transverse momenta have been calculated and they are plotted in Figure 5. While the theoretical plots are agreeable in low-![]() regions, they disagree in high-
regions, they disagree in high-![]() .
.
Now, let us sum up our observations in the following points: 1) The model under consideration here explains the data modesly well on ![]() collisions at
collisions at ![]() TeV. 2) The particle production in heavy ion collisions can be viewed alternatively by this Sequential Chain Model.
TeV. 2) The particle production in heavy ion collisions can be viewed alternatively by this Sequential Chain Model.
Acknowledgements
The work is supported by University Grants Commission, India, against the order no. PSW-30/12(ERO) dt.05 Feb-13.
NOTES
*Corresponding author.