Influence of Ca Content on Binding Energy and Cooper Pairing in Y1-xCaxBa2Cu3O7-δ Compound ()
1. Introduction
To find out what exactly underlies the superconductivity in cuprate HTSC, we first require an in-depth understanding of the cuprate pairing mechanism. One of the first theories was Anderson’s “Resonating Valence Bond (RVB) Theory” [1] , which explained the magnetic pairing due to the strong Coulomb repulsion in a two-dimen- sional (2D) quantum spin-1/2 system [2] - [4] .
The tremendous efforts to unveil high temperature superconductivity (HTSC) have been devoted to the research of the mechanism underlying Cooper pairs which, however, remains a mysterious subject of vigorous debate, and leaves alone many other mysteries like the pseudo gap state, the unnegligible electron-phonon interaction, the universal nodal Fermi velocity, etc. Most of subsequent works bring in more controversies to the list of mysteries [5] .
In high temperature superconductor (HTS) materials, the Cooper pairs are carriers of the superconducting current. Fermi surface pockets were found in quantum oscillations of hall coefficient [5] . However, high critical temperature 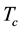 low order parameter, and the unconventional isotopic effect indicate that the phonon mechanism of pairing is not applicable. In the HTS cuprates, two separate energy gaps exist [6] [7] . The CuO2 layers are responsible for superconductivity, and the electrons are concentrated in them. Reduction of number of CuO2 layers in the ultra-thin films leads to decrease in
low order parameter, and the unconventional isotopic effect indicate that the phonon mechanism of pairing is not applicable. In the HTS cuprates, two separate energy gaps exist [6] [7] . The CuO2 layers are responsible for superconductivity, and the electrons are concentrated in them. Reduction of number of CuO2 layers in the ultra-thin films leads to decrease in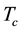 . Furthermore, superconductivity vanishes when less than two layers are left [8] , indicating that superconductivity emerges from some interlayer effects. Seemingly, this contradicts with the results obtained from interface superconductivity where the single CuO2 layer is responsible for superconductivity. However, superconductivity emerges only in the presence of the interfacing material, providing another layer [8] .
. Furthermore, superconductivity vanishes when less than two layers are left [8] , indicating that superconductivity emerges from some interlayer effects. Seemingly, this contradicts with the results obtained from interface superconductivity where the single CuO2 layer is responsible for superconductivity. However, superconductivity emerges only in the presence of the interfacing material, providing another layer [8] .
In this study, the effect of increase of Ca content on the tunneling mechanism of holes between the two CuO2 layers in the YBCO superconductor will be investigated and as well as its effect on the binding energy of the Cooper pairs and the conduction current in the superconductor.
2. Theoretical
In this study, we try to find the effect of Ca content on the binding energy in the superconductor 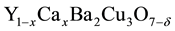 The pairing mechanism of the Cooper pairs for layered HTS materials based on attraction between electrons from adjacent layers is proposed [6] , by using the idea of rigged quantum well considering the oxygen atom as forming the rigged in the CuO2 layer. Which are considered as forming potential wells, but this wells and due to the presence of O atoms will contains ridges, which expand the Fermi sphere, this sphere will undergoes contraction when the two CuO2 layers are close enough to form correlated quantum states (CQS). The Cooper pairs formed by image forces which supply the electron-electron attraction, are comprising the inter- tunneling electrons which will occupy the above states. Tunneling occurs when the distance (d) between the two CuO2 layers (or their potential wells) are short enough, so that tunneling probability are high enough to imitate tunneling. The positive image of the tunneling electron inside the second well will attract another electron, thus Cooper pair are formed from the tunneled electron and the other electron in the second well.
The pairing mechanism of the Cooper pairs for layered HTS materials based on attraction between electrons from adjacent layers is proposed [6] , by using the idea of rigged quantum well considering the oxygen atom as forming the rigged in the CuO2 layer. Which are considered as forming potential wells, but this wells and due to the presence of O atoms will contains ridges, which expand the Fermi sphere, this sphere will undergoes contraction when the two CuO2 layers are close enough to form correlated quantum states (CQS). The Cooper pairs formed by image forces which supply the electron-electron attraction, are comprising the inter- tunneling electrons which will occupy the above states. Tunneling occurs when the distance (d) between the two CuO2 layers (or their potential wells) are short enough, so that tunneling probability are high enough to imitate tunneling. The positive image of the tunneling electron inside the second well will attract another electron, thus Cooper pair are formed from the tunneled electron and the other electron in the second well.
The single CuO2 layer is responsible for superconductivity [6] , However, superconductivity emerges only in the presence of the interfacing material, providing another layer. In his study [6] , the possible pairing mechanism based on single-electron tunneling between CuO2 layers, is proposed. Ridges impose additional boundary conditions on the electron wave function and some quantum states become forbidden. Rejected electrons occupy quantum states with higher energies. The Fermi vector, 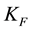 and Fermi energy,
and Fermi energy, 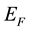 , are increased in the ridged geometry [11] which can be termed as Fermi sphere expansion
, are increased in the ridged geometry [11] which can be termed as Fermi sphere expansion 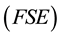 for convenience. In the above study Pairing mechanism is based on the assumption that CuO2 layers, like ridged films, exhibit FSE. The cuprate material contains CuO2 layers, each containing electron gas modified by FSE due to interaction of the adjacent two CuO2 layers, through single-electron tunneling. Cooper pairs exist in correlated quantum states
for convenience. In the above study Pairing mechanism is based on the assumption that CuO2 layers, like ridged films, exhibit FSE. The cuprate material contains CuO2 layers, each containing electron gas modified by FSE due to interaction of the adjacent two CuO2 layers, through single-electron tunneling. Cooper pairs exist in correlated quantum states 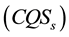 and such states belong to the system of two or more CuO2 layers. The electron-electron attraction originates from the image force [6] .
and such states belong to the system of two or more CuO2 layers. The electron-electron attraction originates from the image force [6] .
Figure 1 shows a reference quantum well layer (a) and a ridged quantum well (RQW) layer (b), and the corresponding energy diagrams. The ridges have depth a and period 2w. The thickness of reference well layer
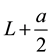 is chosen so that the two layers have the same volume (per unit area). Owing to ridges, some quantum
is chosen so that the two layers have the same volume (per unit area). Owing to ridges, some quantum
states become forbidden in an RQW. The addition of Ca will lead to the decrease of the distance between the two CuO2 layers and thus decreases the rigged height as a result this shown in Figure 1(c) also shown decrease of the Fermi surface expansion and thus lead to decease energy of the system as in the lower part of Figure 1(c).
In RQW the total energy of the electrons is increased with respect to reference QW. The electron gas in RQW is an excited system. If there was some external mechanism to allow back the forbidden quantum states (QS),
![]()
Figure 1. (a) Reference quantum well layer and its energy diagram; (b) RQW layer and its energy diagram [6] (Tavkhelidze, 2010); (c) The effect of Ca addition will decrease the rigged height and thus lowers Fermi surface expansion. The dashed energy levels are the forbidden levels.
then the electrons would occupy them and would get decreased. Tunneling to another RQW is considered as a possible mechanism of energy minimization [6] . Adding another RQW reduces the total energy of the electron gas. Closer it is placed; the higher is the probability of tunneling. The probability of the electron being in the reestablished QS increases with the decreasing distance between the wells as shown in Figure 2(a) Addition of Ca will decrease the distance between the layers this will introduce mechanism to minimize of the energy of the system of the two layers
In cuprates, O and Cu atoms are shifted up and down, relative to the common plane of CuO2 layer, geometry of the layer is akin to the periodic ridges of Ridged Potential Energy Box (RPEB), in the first approximation, a CuO2 layer (for all cuprates) can be regarded as an RPEB-containing electron gas, and the layer has forbidden QS and expanded Fermi sphere.
Figure 2(a) shows two CuO2 layers separated by distance d decreasing d will increase the probability of tunneling and thus minimize energy. addition of Ca will shift the O atom up and down in the two layers of YBCO crystal and thus decreases the distances between the layers, Figure 2(b) show the effect of Ca addition on the distance between the two planes which will be decreased, as a result the energy of the system of the two layers will be decreasing by lowering energy levels. Decrease distance between the two planes will enhance the tunneling process mechanism and increasing conduction current by due to increasing Ca content.
The density of quantum state, tunneling probability and binding energy can be calculated as follows (L. X. You et al. 2005):
The density of QSs as found in is 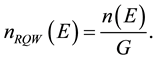
Density of quantum states can be determined as follows:
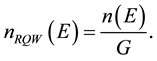 (1)
(1)
Here 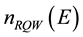 is density of QS in RPEB,
is density of QS in RPEB, 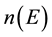 is density of QS in conventional PEB
is density of QS in conventional PEB  is geometry factor and E is electron energy.
is geometry factor and E is electron energy.
The density of forbidden QS is
 (2)
(2)
Each electron that leaves Fermi level to CQS, can be in four possible quantum states, ![]() ,
, ![]() and
and![]() . Therefore, CQS energy level degeneracy is 4 CQS contains tunneling electrons. Tunneling probability is
. Therefore, CQS energy level degeneracy is 4 CQS contains tunneling electrons. Tunneling probability is
![]() (3)
(3)
The substitution of Ca instead of Y will deceases the distance between the layers and Equation (3) must be modified as follows:
![]() (3a)
(3a)
![]() (a) (b)
(a) (b)
Figure 2. (a) The CQS (dotted lines) occupied by Cooper pairs CuO2 layers separated by distance d. The density of QSs as found; (b) The effect of Ca addition will decrease the distance between the two CuO2 layers and thus lowering the energy levels and increasing current.
Probability of electron being in CQS is equal to tunneling probability and layer binding energy density (per unit volume) within the energy interval of δE will be:
![]() (4)
(4)
Here, ![]() is reduction of energy per electron in the process of CQS formation Figure 3.
is reduction of energy per electron in the process of CQS formation Figure 3.
Integration of Equation (4) over energy range below Fermi energy gives
![]() (5)
(5)
![]() is layer binding energy density, inserting Equation (2) in Equation (5) gives
is layer binding energy density, inserting Equation (2) in Equation (5) gives
![]() (6)
(6)
![]() (7)
(7)
inserting Equation (7) in Equation (6) obtained
![]() (8)
(8)
Finally inserting Equation (4) in Equation (9) and G = 1 gives the binding energy
![]() (9)
(9)
In this research the binding energy in ![]() (YBCCO) compound will be found considering the effect of increasing of the Ca content, first of all the change in distance between the two CuO2 layers by addition of Ca content instead of Yttrium into compound must be determined. The original distance between the two CuO2 planes before the addition of Ca is (3.18) Å in the
(YBCCO) compound will be found considering the effect of increasing of the Ca content, first of all the change in distance between the two CuO2 layers by addition of Ca content instead of Yttrium into compound must be determined. The original distance between the two CuO2 planes before the addition of Ca is (3.18) Å in the ![]() (YBCO), but the substitution of the compound by Ca3+ instead of Y3+ will decrease the distance between the layers [9] [10] , to calculate the decease it is important to consider the change in the distances between two CuO2 layers by the addition of Ca in
(YBCO), but the substitution of the compound by Ca3+ instead of Y3+ will decrease the distance between the layers [9] [10] , to calculate the decease it is important to consider the change in the distances between two CuO2 layers by the addition of Ca in ![]() as in Figure 3 because [O(2) or Cu2] atoms shifted up and down in the CuO2 planes vertically away from the CuO chains toward the planes in the upper and lower in the YBCCO crystal with addition of Ca content, the vertical distance change, by subtraction vertical change in both side from the original distance between the two planes (3.18 Å) the decreasing in the distance between the two CuO2 planes after addition Ca content from (0 to 0.2) the result as shown in the Table 1.
as in Figure 3 because [O(2) or Cu2] atoms shifted up and down in the CuO2 planes vertically away from the CuO chains toward the planes in the upper and lower in the YBCCO crystal with addition of Ca content, the vertical distance change, by subtraction vertical change in both side from the original distance between the two planes (3.18 Å) the decreasing in the distance between the two CuO2 planes after addition Ca content from (0 to 0.2) the result as shown in the Table 1.
![]() (a) (b)
(a) (b)
Figure 3. (a) and (b) Schematic diagram of two different model of crystal structure of YBCO compound [12] .
![]()
Table 1. Relation of the distance between the two CuO2 layer and tunneling probability of holes.
The tunneling probability of the holes between the two CuO2 layers being increasing with decreasing the distance between layers which can be calculated using the Equation (3) and the result are shown in the Table 1.
The calculation of the binding energy was done by using Equation (9), for solving the integration we apply the math lab program to determine each value of binding energy which corresponding to concentration of Ca content in the compound. The results are shown in the Table 2. Which shows that Ca content increases the distance between the two layers decrease as a result the binding energy will be decreased as seen in the Figure 4 and Figure 5 in the ![]() compound. The following experimental values were inserted in Equation (9): for a work function, ϕ = 4 eV for Fermi energy = U − ϕ = 300 meV.
compound. The following experimental values were inserted in Equation (9): for a work function, ϕ = 4 eV for Fermi energy = U − ϕ = 300 meV.
3. Results
In this study the effect of Ca content in the ![]() compound on the binding energy between the holes in CuO2 planes is investigated, many other parameters are affected by changing of the Ca content such as lattice parameters, critical temperature, crystal structure and etc., and by using the above parameters and their change the effect of Ca content on the distance between CuO2 layers are calculated [13] [14] .
compound on the binding energy between the holes in CuO2 planes is investigated, many other parameters are affected by changing of the Ca content such as lattice parameters, critical temperature, crystal structure and etc., and by using the above parameters and their change the effect of Ca content on the distance between CuO2 layers are calculated [13] [14] .
![]()
Table 2. Relation between Ca content, distance between the CuO2 planes after substitution of Ca2+ instead Y3+ and binding energy.
![]()
![]() (a) (b)
(a) (b)
Figure 4. (a) Shows the variation of binding energy and dCu2-Cu2 distance as a function of Ca content; (b) Shows the variation of binding energy (meV) and energy gap as a function of Ca content in ![]() compound.
compound.
![]()
![]() (a) (b)
(a) (b)
Figure 5. (a) Shows the variation of binding energy and hole concentration as a function of Ca content; (b) Shows the variation of binding energy and current density as a function of Ca content in ![]() compound.
compound.
Figure 4(a) shows the relation between binding energy and the distance between CuO2-CuO2 two planes as a function of Ca content. As Ca content is increasing the distance between the two CuO2 planes will be decreased and as a result the binding energy of the system will be decreased also. This is combined with a shift of Cu(2) away from the single chain, and therefore the CuO2-CuO2 distance decreases.
Figure 4(b) shows the relation between binding energy and energy gap of the system as a function of Ca content which indicate as Ca content increased energy gap of the superconductors will be decreased as a result the binding energy will be decreased.
Figure 5(a) shows the relation between binding energy and hole concentration in the two CuO2 planes as a function of Ca content which indicates that: as Ca content increased the binding energy decreases as a result the hole concentration will be increased.
Figure 5(b) shows the relation between binding energy and current density in the two CuO2 planes as a function of Ca content which indicates that as Ca content increases the binding energy decreases in superconductors system and the current density will be increased.
Figure 6(a) shows the relation between binding energy and hole concentration as a function of energy gap which indicates that the binding energy increases and hole concentration decreases with increasing energy gap.
Figure 6(b) shows the relation between binding energy and current density as a function of energy gap which indicates that the binding energy increases and current density decreases with increasing energy gap.
Figure 7 shows the relation between critical temperature and binding energy as a function Ca content as Ca content its clear that both decreasing with increasing of Ca content this is a logical result because there is a direct relation between binding energy and critical temperature.
![]()
![]() (a) (b)
(a) (b)
Figure 6. (a) The variation of binding energy and hole concentration; (b) The variation of binding energy and current density as a function of energy gap in ![]() .
.
![]()
Figure 7. The variation of critical temperature and binding energy as a function of Ca content in![]() .
.
4. Discussion
In this research the model we propose for the influence of calcium content on the binding energy and Cooper pairing due to the decrease of separation between the two CuO2 layers gives good results which explains the experimental facts about increase of superconducting current, and decrease of Tc for the high temperature superconductor ![]() . Calculations of the binding energy using the modified equation [6] enable us to find relations between binding energy and important superconducting quantities depending on essential suggestion that: the Ca2+ substitution for Y3+ lead to decreasing the distance between the two CuO2 layers and hence potential energy of the system will be decreased, this will lead to decreasing the binding energy between the Cooper pairs, also decreasing the distance between the two CuO2 layers increasing the tunneling probability of holes between the two CuO2 layers (considering the two layers as a rigged quantum well) and thus increasing conduction mechanism by increasing current density. Also addition of Ca instead of yttrium will decrease the energy gap and as a result will decrease the critical temperature.
. Calculations of the binding energy using the modified equation [6] enable us to find relations between binding energy and important superconducting quantities depending on essential suggestion that: the Ca2+ substitution for Y3+ lead to decreasing the distance between the two CuO2 layers and hence potential energy of the system will be decreased, this will lead to decreasing the binding energy between the Cooper pairs, also decreasing the distance between the two CuO2 layers increasing the tunneling probability of holes between the two CuO2 layers (considering the two layers as a rigged quantum well) and thus increasing conduction mechanism by increasing current density. Also addition of Ca instead of yttrium will decrease the energy gap and as a result will decrease the critical temperature.
We can say that: Ca2+ substitution for Y3+ change the order of the single Cu-O chains as a result buckling in the CuO2 plane is diminished due to decrease of potential energy, therefore the CuO2-CuO2 distance decreases as a result the holes tunneling between the two plane increases by decreasing the distances between the two potential wells of the layers. All the relation we find between Ca content and energy gap, binding energy hole concentration etc. ensures the above and in favor of the mechanism suggested for the Cooper pairing.
5. Conclusions
1) Ca addition to the YBCO compound leads to decreasing the distance between the two CuO2 layers as a result of diminishing of buckling in the CuO2 plane, and this lowers the potential energy of the system.
2) Decreasing the distance between the CuO2 two layers will enhance the tunneling process and enhance formation of Cooper pairs. This will increase the superconducting current.
3) Ca addition will decrease the binding energy and this will increase hole concentration and thus will increase conduction mechanism.
4) Increasing Ca content will decrease the energy gap and as a result will decrease the critical temperature.
5) Increasing superconducting current is a great practical goal, but Tc decreases. Our future work will concentrate on increasing current without decreasing Tc.