Argument Estimates of Multivalent Functions Involving a Certain Fractional Derivative Operator

Jae Ho Choi^*

Department of Mathematics Education, Daegu National University of Education, Daegu, South Korea.

DOI: 10.4236/apm.2015.52011                

Abstract

The object of the present paper is to investigate various argument results of analytic and multivalent functions which are defined by using a certain fractional derivative operator. Some interesting applications are also considered.

Keywords

Multivalent Analytic Functions, Argument, Integral Operator, Fractional Derivative Operator

1. Introduction

Let 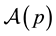denote the class of functions of the form

(1.1)

which are analytic in the open unit disk. Also let 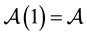denote the class of all analytic functions 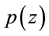with which are defined on.

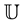Let a, b and c be complex numbers with. Then the Gaussian hypergeometric function 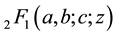is defined by

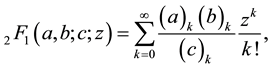(1.2)

where 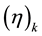is the Pochhammer symbol defined, in terms of the Gamma function, by

The hypergeometric function 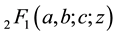is analytic in 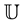and if a or b is a negative integer, then it reduces to a polynomial.

There are a number of definitions for fractional calculus operators in the literature (cf., e.g., [1] and [2] ). We use here the Saigo type fractional derivative operator defined as follows ([3] ; see also [4] ):

Definition 1. Let 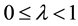and. Then the generalized fractional derivative operator of a function is defined by

(1.3)

The function is an analytic function in a simply-connected region of the z-plane containing the origin, with the order

for, and the multiplicity of is removed by requiring that to be real when.

Definition 2. Under the hypotheses of Definition 1, the fractional derivative operator of a function is defined by

(1.4)

With the aid of the above definitions, we define a modification of the fractional derivative operator by

(1.5)

for and. Then it is observed that also maps onto itself as follows:

(1.6)

It is easily verified from (1.6) that

(1.7)

Note that, and, where is the fractional derivative operator defined by Srivastava and Aouf [5] .

In this manuscript, we drive interesting argument results of multivalent functions defined by fractional derivative operator.

2. Main Results

In order to establish our results, we require the following lemma due to Lashin [6] .

Lemma 1 [6] . Let be analytic in, with and . Further suppose that and

(2.1)

then

(2.2)

We begin by proving the following result.

Theorem 1. Let, and, and let. Suppose that satisfies the condition

(2.3)

then

(2.4)

Proof. If we define the function by

(2.5)

then is analytic in, with and. Making use of the logarithmic differentiation on both sides of (2.5), we have

(2.6)

By applying the identity (1.7) in (2.6), we observe that

Hence, by using Lemma 1, we conclude that

which completes the proof of Theorem 1.

Remark 1. Putting, and in Theorem 1, we obtain the result due to Lashin ([6] , Theorem 2.2).

Taking and in Theorem 1, we have the following corollary.

Corollary 1. Let, and. Suppose that satisfies the condition

then

Theorem 2. Let, , and. Suppose that satisfies the condition

(2.7)

then

(2.8)

Proof. If we set

(2.9)

then is analytic in, with and. By using the logarithmic differentiation on both sides of (2.9), we obtain

Thus, in view of Lemma 1, we have

which evidently proves Theorem 2.

Remark 2. Setting and in Theorem 2, we get the result obtained by Goyal and Goswami ([7] , Corollary 3.6).

Putting in Theorem 2, we obtain the following result.

Corollary 2. Let. Suppose that satisfies the condition

then

Finally, we consider the generalized Bernardi-Libera-Livingston integral operator defined by (cf. [8] [9] and [10] )

(2.10)

Theorem 3. Let, , and, and let. Suppose that satisfies the condition

(2.11)

then

(2.12)

Proof. From (2.10) we observe that

(2.13)

If we let

(2.14)

then is analytic in, with and. Differentiating both sides of (2.14) logarithmically, it follows that

(2.15)

Hence, by applying the same arguments as in the proof of Theorem 1 with (2.13) and (2.15), we obtain

which proves Theorem 3.

Acknowledgements

This work was supported by Daegu National University of Education Research Grant in 2014.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Srivastava, H.M. and Buschman, R.G. (1992) Theory and Applications of Convolution Integral Equations. Kluwer Academic Publishers, Dordrecht, Boston and London.
[2]	Samko, S.G., Kilbas, A.A. and Marichev, O.I. (1993) Fractional Integral and Derivatives, Theory and Applications. Gordon and Breach, New York, Philadelphia, London, Paris, Montreux, Toronto and Melbourne.
[3]	Raina, R.K. and Srivastava, H.M. (1996) A Certain Subclass of Analytic Functions Associated with Operators of Fractional Calculus. Computers & Mathematics with Applications, 32, 13-19. http://dx.doi.org/10.1016/0898-1221(96)00151-4
[4]	Raina, R.K. and Choi, J.H. (2002) On a Subclass of Analytic and Multivalent Functions Associated with a Certain Fractional Calculus Operator. Indian Journal of Pure and Applied Mathematics, 33, 55-62.
[5]	Srivastava, H.M. and Aouf, M.K. (1992) A Certain Fractional Derivative Operator and Its Applications to a New Class of Analytic and Multivalent Functions with Negative Coefficients. I and II. Journal of Mathematical Analysis and Applications, 171, 1-13.
[6]	Lashin, A.Y. (2004) Applications of Nunokawa’s Theorem. Journal of Inequalities in Pure and Applied Mathematics, 5, 1-5. Art. 111.
[7]	Goyal, S.P. and Goswami, P. (2010) Argument Estimate of Certain Multivalent Analytic Functions Defined by Integral Operators. Tamsui Oxford Journal of Mathematical Sciences, 25, 285-290.
[8]	Bernardi, S.D. (1969) Convex and Starlike Univalent Functions. Transaction of the American Mathematical Society, 135, 429-446. http://dx.doi.org/10.1090/S0002-9947-1969-0232920-2
[9]	Libera, R.J. (1965) Some Classes of Regular Univalent Functions. Proceedings of the American Mathematical Society, 16, 755-758. http://dx.doi.org/10.1090/S0002-9939-1965-0178131-2
[10]	Srivastava, H.M. and Owa, S. (Eds.) (1992) Current Topics in Analytic Function Theory. World Scientific Publishing Company, Singapore, New Jersey, London, and Hong Kong.