1. Introduction
Recently, eigenvalue problems for tensors have gained special attention in the realm of numerical multilinear algebra [1] -[4] , and they have a wide range of practical applications [5] [6] . The definition of eigenvalues of square tensors has been introduced in [7] -[9] . Nice properties such as the Perron-Frobenius theorem for eigenvalues of nonnegative square tensors [7] have been discussed. The authors give algorithms to compute the largest eigenvalue of a nonnegative square tensor in [6] [10] . Singular values of rectangular tensors have been introduced in [11] . In [11] [12] , properties of singular values of rectangular tensors have been discussed. In particular, Chang, Qi and Zhou [11] established the Perron-Frobenius theorem to singular values of nonnega- tive rectangular tensors. They also proposed an iterative algorithm to find the largest singular value of a nonne- gative rectangular tensor. In [13] , the authors studied the convergence of the proposed algorithm.
In this paper, we focus on the tensor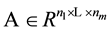 , and study properties of H-singular values of a positive tensor
, and study properties of H-singular values of a positive tensor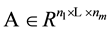 . For more about the definition of the H-singular value of a tensor
. For more about the definition of the H-singular value of a tensor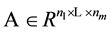 , one can turn to the paper [14] .
, one can turn to the paper [14] .
The paper is organized as follows. In Section 2, we recall some definitions and define H-singular values for a positive tensor, we extend the Perron-Frobenius theorem to H-singular values of positive tensors. In Section 3, we give an algorithm to find the largest singular value of a positive tensor, some numerical experiments are given to show that our algorithm is efficient.
2. H-Singular Values for a Tensor
Let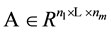 . In this paper, we extend the definition of the classical concept of rectangular tensors, the tensors are no need square or rectangular. Consider the optimization problem
. In this paper, we extend the definition of the classical concept of rectangular tensors, the tensors are no need square or rectangular. Consider the optimization problem
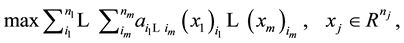 (1)
(1)
under the constraints that
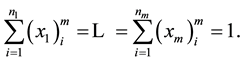
We obtain the following system at a critical point:
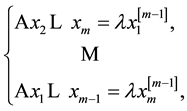 (2)
(2)
where
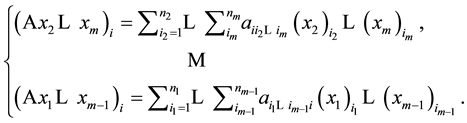
If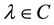 ,
, 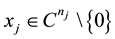 are solutions of (2), then we say that
are solutions of (2), then we say that 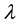 is an H-singular value of the tensor
is an H-singular value of the tensor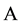 ,
,  are eigenvectors of
are eigenvectors of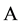 , associated with the H-singular value
, associated with the H-singular value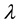 .
.
Let
![]()
![]()
A vector ![]() is called nonnegative if
is called nonnegative if ![]() and it is called strongly positive if
and it is called strongly positive if![]() . For any
. For any![]() , let
, let ![]() be a nonnegative vector. We give our main theorems as follows.
be a nonnegative vector. We give our main theorems as follows.
Lemma 1. If a tensor ![]() is positive, then for any
is positive, then for any![]() ,
, ![]() ,
,
![]() (3)
(3)
Proof. If![]() ,
, ![]() , suppose
, suppose![]() , and then
, and then![]() , a contradiction.
, a contradiction.
If![]() , and
, and![]() ,
, ![]() , there exists
, there exists![]() , and we can get
, and we can get
![]()
Then
![]()
Similarly, we can get![]() .
. ![]()
Lemma 2. Let a tensor ![]() be positive, and let
be positive, and let ![]() be a
be a
solution of (2). If ![]() satisfies
satisfies
![]() (4)
(4)
Then![]() .
.
Proof. Define![]() . Since
. Since![]() ,
,![]() . We have
. We have
![]()
if and only if![]() . Thus
. Thus
![]()
i.e.,
![]()
This implies![]() .
. ![]()
Remark. If there exists ![]() such that
such that
![]() (5)
(5)
Then ![]() is the eigenvalue of
is the eigenvalue of ![]() and
and ![]() is the corresponding eigenvectors of
is the corresponding eigenvectors of![]() ,
,![]() . This re- mark can be obtained by similar process in [12] [15] .
. This re- mark can be obtained by similar process in [12] [15] .
Theorem 1. Assume that a tensor ![]() is positive, then there exists a solution
is positive, then there exists a solution ![]() of
of
system (1), satisfying ![]() and
and![]() , Moreover, if
, Moreover, if ![]() is a singular value with strongly positive ei-
is a singular value with strongly positive ei-
genvectors![]() ,
, ![]() , then
, then![]() , The strongly positive eigenvectors are unique up to a multiplica-
, The strongly positive eigenvectors are unique up to a multiplica-
tive constant,
Proof. Denote![]() . Provide by Lemma 1, the map F on
. Provide by Lemma 1, the map F on ![]() into itself:
into itself:
![]()
is well defined.
According to the Brouwer Fixed Point Theorem, there exists ![]() such that
such that
![]() (6)
(6)
where
![]()
Let
![]()
Then ![]() is a solution of (2).
is a solution of (2).
Let us show:![]() . If not, suppose
. If not, suppose![]() , that is to say,
, that is to say,
![]()
this contradicts the result of Lemma 1. Therefore,
![]()
The uniqueness of the positive singular value with strongly positive left and right eigenvectors now follows from Lemma 2 directly. The uniqueness up to a multiplicative constant of the strongly positive left and right eigenvectors is proved in the same way as in [7] . ![]()
Theorem 2. Assume that ![]() is a positive tensor, then
is a positive tensor, then
![]()
where ![]() is the unique positive singular value corresponding to strongly positive eigenvectors.
is the unique positive singular value corresponding to strongly positive eigenvectors.
Proof. Let![]() ,
,![]() . We define
. We define
![]()
Since it is a positively 0-homogeneous function, it can be restricted on![]() . Let
. Let
![]()
Let ![]() is a solution of (2). On one hand, we have
is a solution of (2). On one hand, we have
![]()
On the other hand, by the definition of![]() , we get
, we get
![]()
This means
![]() (7)
(7)
According to Lemma 2, we have![]() , and the we get
, and the we get
![]()
Similarly, we prove the other equality. ![]()
Theorem 3. Assume that ![]() is a positive tensor, and
is a positive tensor, and ![]() is the positive singular value with strongly positive eigenvectors. Then
is the positive singular value with strongly positive eigenvectors. Then ![]() for all singular values
for all singular values ![]() of
of![]() .
.
Proof. Let ![]() for some
for some![]() ,
,![]() . We wish to show
. We wish to show![]() . Let
. Let![]() . We get
. We get
![]()
Apply Theorem 2, we can get
![]()
Theorem 4. Suppose that ![]() is a positive tensor satisfying
is a positive tensor satisfying
![]()
where ![]() is a constant. Then
is a constant. Then![]() .
.
Proof. Let ![]() is a solution of (2). Without loss of generality, we suppose that
is a solution of (2). Without loss of generality, we suppose that![]() ,
,![]() . Then
. Then
![]()
On the other hand, it is easy to check that C is an eigenvalue of A with corresponding eigenvectors![]() ,
,![]() . So
. So![]() . Thus we have
. Thus we have![]() .
. ![]()
3. An Iterative Algorithm
In this section, we propose an iterative algorithm to calculate the largest H-singular value of a positive tensor based on Theorem 2 and Theorem 3. This algorithm is a modified version of the one given in [11] [13] , and we will show the convergence of the proposed algorithm for any positive tensor. In this section, we always suppose that ![]() is a positive tensor.
is a positive tensor.
For a positive tensor![]() ,
, ![]() ,
, ![]() , let
, let
![]() (8)
(8)
Algorithm 3.1
Step 0 Choose![]() . Set
. Set![]() ;
;
Step 1 Compute
![]() (9)
(9)
Let
![]() (10)
(10)
![]() (11)
(11)
Step 2 If![]() , then stop. Otherwise, compute
, then stop. Otherwise, compute
![]() (12)
(12)
and replace ![]() by
by ![]() and go to Step 1.
and go to Step 1.
In the following, we will give a convergence result for Algorithm 3.1.
Theorem 5. Assume that ![]() is a solution of (2). Then,
is a solution of (2). Then,
![]()
Proof. By (8),![]() . From Theorem 2, for
. From Theorem 2, for ![]()
![]()
We now prove for any![]() ,
,
![]()
For each![]() , by the definition of
, by the definition of ![]() and Lemma 1, we have
and Lemma 1, we have
![]()
Then,
![]()
So,
![]()
Hence, we get
![]()
which means for ![]()
![]()
Therefore, we get
![]()
Similarly, we can prove that
![]()
From Theorem 5, ![]() is a monotonic increasing sequence and it has an upper bound, so the limit exists. Since
is a monotonic increasing sequence and it has an upper bound, so the limit exists. Since ![]() is monotonic decreasing sequence and it has a lower bound, the limit exists as well. We suppose
is monotonic decreasing sequence and it has a lower bound, the limit exists as well. We suppose
![]()
By Theorem 5, we have
![]() (13)
(13)
The argument used in the following proof is parallel to that in [13] . We proceed the proof for completeness.
Theorem 6. Let![]() ,
, ![]()
![]() be the sequences produced by Algorithm 3.1. Then
be the sequences produced by Algorithm 3.1. Then
a) ![]() have convergent subsequences which converge to
have convergent subsequences which converge to![]() , respectively. Moreover,
, respectively. Moreover, ![]() ,
,![]() .
.
b) ![]()
c)![]() .
.
Proof. As ![]() for all
for all![]() . Hence, there exists a convergent subsequence by the com-
. Hence, there exists a convergent subsequence by the com-
pactness of the unit ball in ![]() and
and ![]() must not be a zero vector.
must not be a zero vector.
By the continuity of![]() , (8) and (9), we get the result (b).
, (8) and (9), we get the result (b).
If![]() , we get that someone of the follow inequations exists:
, we get that someone of the follow inequations exists:
![]() . By Theorem 2.5 in [13] , there exists a positive integer
. By Theorem 2.5 in [13] , there exists a positive integer
![]() such that
such that
![]()
By (a) and the continuity of![]() , for any sufficiently large
, for any sufficiently large![]() , we obtain
, we obtain
![]()
Then we obtain![]() , which contradicts with Theorem 5. So (c) holds.
, which contradicts with Theorem 5. So (c) holds. ![]()
By Theorem 6, we can get the largest H-singular value of ![]() is
is
![]()
In the following, in order to show the viability of Algorithm 3.1, we used Matlab 7.1 to test it with some randomly generated rectangular tensors. For these randomly generated tensors, the value of each entry is be- tween 0 and 10. we set![]() . We terminated our iteration when
. We terminated our iteration when![]() .
.
Our numerical results are shown in Table 1. In this table, Ite denotes the number of iterations, ![]() and λ denote the values of
and λ denote the values of ![]() and
and ![]() at the final iteration, respectively.
at the final iteration, respectively. ![]() denote the values of at the final iteration, respectively. The results in Table 1 show that the proposed algorithm is promising. The algorithm is able to produce the largest singular values for all these randomly generated posi-
denote the values of at the final iteration, respectively. The results in Table 1 show that the proposed algorithm is promising. The algorithm is able to produce the largest singular values for all these randomly generated posi-
![]()
Table 1. Numerical results of Algorithm 3.1 for randomly generated tensors.
tive tensors.
4. Conclusion
In this paper, we give some eigenvalues properties about the H-singular value of a positive tensor ![]() introduced in [6] . We find that the Perron-Frobenius like theorem for nonnegative square tensors can not be extended to the nonnegative tensor
introduced in [6] . We find that the Perron-Frobenius like theorem for nonnegative square tensors can not be extended to the nonnegative tensor![]() , so here we limit the tensor
, so here we limit the tensor ![]() to the positive case. An algorithm is given to compute the largest H-singular value of the positive tensor.
to the positive case. An algorithm is given to compute the largest H-singular value of the positive tensor.
Acknowledgements
I thank the editor and the referee for their comments. The author is funded by the Fundamental Research Funds for Central Universities.