Idempotent and Regular Elements of the Complete Semigroups of Binary Relations of the Class ∑3(X,9) ()
1. Introduction
Let X be a nonempty set and BX be semigroup of all binary relations on the set X. If D is a nonempty set of subsets of X which is closed under the union then D is called a complete X-semilattice of unions.
Let f be an arbitrary mapping from X into D. Then one can construct a binary relation  on X by
on X by
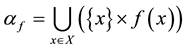 . The set of all such binary relations is denoted by
. The set of all such binary relations is denoted by 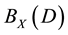 and called a complete semi- group of binary relations defined by an X-semilattice of unions D.
and called a complete semi- group of binary relations defined by an X-semilattice of unions D.
We use the notations, 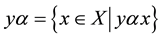 ,
, 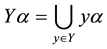 ,
, 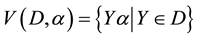 ,
, .
.
A representation of a binary relation 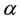 of the form
of the form 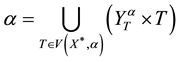 is called quasinormal. Note that, if
is called quasinormal. Note that, if  is a quasinormal representation of the binary relation
is a quasinormal representation of the binary relation , then
, then  for T,
for T,
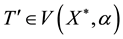 and
and .
.
A complete X-semilattice of unions D is an XI-semilattice of unions if 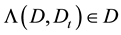 for any
for any  and
and
![]() for any nonempty element Z of D.
for any nonempty element Z of D.
Now, ![]() is said to be right unit if
is said to be right unit if ![]() for all
for all![]() . Also,
. Also, ![]() is idempotent if
is idempotent if![]() . And
. And ![]() is said to be regular if
is said to be regular if ![]() for some
for some![]() .
.
Let D', D'' be complete X-semilattices of unions and ![]() be a one-to-one mapping from D' to D''. A mapping
be a one-to-one mapping from D' to D''. A mapping
![]() is a complete isomorphism provided
is a complete isomorphism provided ![]() for all nonempty subset D1 of the se-
for all nonempty subset D1 of the se-
milattice D'. Besides that, if ![]() is a complete isomorphism where
is a complete isomorphism where![]() ,
, ![]() for all
for all![]() ,
, ![]() is said to be a complete
is said to be a complete ![]() -isomorphism.
-isomorphism.
Let Q and D' be respectively some XI and X-subsemilattices of the complete X-semilattice of unions D. Then
![]()
where ![]() complete isomorphism and
complete isomorphism and![]() . Besides, let us denote
. Besides, let us denote
![]() and
and ![]()
where
![]()
![]()
This structure was comprehensively investigated in Diasamidze [1] .
Lemma 1. [1] If Q is complete X-semilattice of unions and ![]() is the set all right units of the semigroup
is the set all right units of the semigroup ![]() then
then![]() .
.
Lemma 2. [2] Let X be a finite set, D be a complete X-semilattice of unions and ![]() be X-subsemilattice of unions of D satisfies the following conditions
be X-subsemilattice of unions of D satisfies the following conditions
![]()
Q is XI-semilattice of unions.
Theorem 1. [2] Let X be a finite set and Q be XI-semilattice. If ![]() is
is ![]() -iso- morphic to Q and
-iso- morphic to Q and![]() , then
, then
![]()
Theorem 2. [2] Let ![]() be a quasinormal representation of the form
be a quasinormal representation of the form ![]() such that
such that
![]() .
. ![]() is a regular iff for some complete
is a regular iff for some complete ![]() -isomorphism
-isomorphism![]() , the following conditions are satisfied:
, the following conditions are satisfied:
![]()
Let X be a finite set and ![]() be a complete X-semilattice of unions which satisfies the following conditions
be a complete X-semilattice of unions which satisfies the following conditions
![]()
The diagram of the D is shown in Figure 1. By the symbol ![]() we denote the class of all complete X- semilattice of unions whose every element is isomophic to an X-semilattice of the form D.
we denote the class of all complete X- semilattice of unions whose every element is isomophic to an X-semilattice of the form D.
All subsemilattice of ![]() are given in Figure 2.
are given in Figure 2.
In Diasamidze [1] , it has shown that subsemilattices 1 - 15 are XI-semilattice of unions and subsemilattices 17 - 24 are not XI-semilattice of unions. In Yeşil Sungur [3] and Albayrak [4] , they have shown that subsemilattices 25 and 26 are XI-semilattice of unions if and only if![]() ”. Also they found that number of right unit, idempotent and regular elements in subsemilattices.
”. Also they found that number of right unit, idempotent and regular elements in subsemilattices.
In this paper, we take in particular, ![]() subsemilattice of D. We will calculate the number of right unit, idempotent and regular elements
subsemilattice of D. We will calculate the number of right unit, idempotent and regular elements ![]() of
of ![]() satisfied that
satisfied that ![]() for a finite set X. Also we will give a formula for calculate idempotent and regular elements of
for a finite set X. Also we will give a formula for calculate idempotent and regular elements of ![]() defined by an X-semilattice of unions
defined by an X-semilattice of unions![]() .
.
2. Results
Let ![]() be complete X-subsemilattice of D satisfies the following conditions
be complete X-subsemilattice of D satisfies the following conditions
![]()
The diagram of the Q16 is shown in Figure 3. From Lemma 2 Q16 is XI-semilattice of unions.
Let ![]() denote the set of all XI-subsemilattice of the semilattice D which are isomorphic of the X-semi- lattice Q16. Then we get
denote the set of all XI-subsemilattice of the semilattice D which are isomorphic of the X-semi- lattice Q16. Then we get
![]()
Let ![]() be a idempotent element having a quasinormal representation of the form
be a idempotent element having a quasinormal representation of the form
![]() , such that
, such that![]() . First we calculate number of this idempotent elements in
. First we calculate number of this idempotent elements in![]() .
.
Lemma 3. If X is a finite set and ![]() is the set all right units of the semigroup
is the set all right units of the semigroup![]() , then the number
, then the number ![]() may be calculated by formula:
may be calculated by formula:
![]()
Proof. From Lemma 1 we have ![]() where
where ![]() is identity mapping of the set Q16.
is identity mapping of the set Q16.
For this reason ![]() in Theorem 1. Then we obtain
in Theorem 1. Then we obtain
![]()
Theorem 3. If X is a finite set and ![]() is the set all idempotent elements of the semigroup
is the set all idempotent elements of the semigroup![]() , then the number
, then the number ![]() may be calculated by formula:
may be calculated by formula:
![]()
Proof. By using Lemma 3 we have number of right units of the semigroup ![]() defined by
defined by
![]() for
for![]() . Then number of idempotent elements of
. Then number of idempotent elements of ![]() calculated
calculated
by formula![]() . By using
. By using
![]()
we obtain above formula. ![]()
Now we will calculate number of regular elements ![]() having a quasinormal representation of the
having a quasinormal representation of the
form ![]() such that
such that![]() . Let
. Let ![]() be the set all regular elements of the
be the set all regular elements of the
semigroup![]() . By using
. By using ![]() we get
we get ![]() . The number of all automorphisms of the semilattice Q16 is q = 4. These are
. The number of all automorphisms of the semilattice Q16 is q = 4. These are
![]()
Then![]() . Also by using
. Also by using
![]()
we get![]() .
.
Theorem 4. If X is a finite set and ![]() is the set all regular elements of the semigroup
is the set all regular elements of the semigroup![]() , then the number
, then the number ![]() may be calculated by formula:
may be calculated by formula:
![]()
Proof. To account for the elements that are in![]() , we first subtract out intersection of
, we first subtract out intersection of![]() ’s. Let
’s. Let![]() . By using Theorem 2 and
. By using Theorem 2 and ![]()
![]()
We get ![]() which is a contradiction with
which is a contradiction with![]() ,
, ![]() ,
, ![]() ,
, ![]() are dis- joint sets. Then
are dis- joint sets. Then![]() . Smilarly
. Smilarly ![]() for
for![]() . Thus we obtain
. Thus we obtain
![]()
From Theorem 1 we get above formula. ![]()
Corollary 1. If X is a finite set, ID is the set all idempotent elements of the semigroup ![]() and RD is the set all regular elements of the semigroup
and RD is the set all regular elements of the semigroup![]() , then the number
, then the number ![]() and
and ![]() may be calculated by formula:
may be calculated by formula:
![]()
Proof. Let ID be the set of all idempotent elements of the semigroup![]() . Then number of idempotent element of
. Then number of idempotent element of ![]() is equal to sum of idempotent elements of the subsemigroup defined by XI-subsemilattice of D.
is equal to sum of idempotent elements of the subsemigroup defined by XI-subsemilattice of D. ![]() is given in Diasamidze [1] for
is given in Diasamidze [1] for![]() . From Theorem 3 we have number of idempotent elements of the subsemigroup
. From Theorem 3 we have number of idempotent elements of the subsemigroup![]() . Then the number
. Then the number ![]() may be calculated by formula
may be calculated by formula
![]() . Similarly the number
. Similarly the number ![]() may be calculated by formula
may be calculated by formula![]() .
. ![]()