Modeling the Rheological Characteristics of Flexible High-Yield Pulp-Fibre-Reinforced Bio-Based Nylon 11 Bio-Composite ()
1. Introduction
Pulp-fibre-reinforced thermoplastic composites are in high demand in the automobile, construction, and aerospace industries. Vegetable fibres are biodegradable and renewable; they consume less energy than glass fibres, and consequently they generate less pollution [1] -[3] . Other reasons for the high demand for the utilization of green fibres are their low density and good thermal and acoustic properties. Pulp fibres, moreover, do not abrade processing tools [2] [3] . Materials from biological sources regroup natural polymers, so they can be expected to exhibit viscoelastic behavior. Appropriate processing and production conditions of polymer products are determined by their rheological characteristics. The bleached high-yield pulp (HYP) fibres derived from hardwood that were used in this study are short crystalline fibres [4] [5] . Short-fibre-reinforced polymer composites are extensively used in manufacturing industries due to their light weight and improved mechanical properties [5] . Hence, HYP has been used not only for its low lignin content, but also for its potential thermal stability and its strong adhesion when it is bonded with high-temperature engineering thermoplastic polymers [4] - [6] .
The study of the rheological behavior of viscoelastic polymer composites is mostly limited to a two-phase fibre-polymer. The so-called interphase zone appears in the viscoelastic damping of polymer composite processing [7] . This deformation significantly affects the predicted overall rheological characteristics of natural-fibre- reinforced thermoplastic composites [8] . During processing, fibre-reinforced polymers are subjected to rigorous deformations that cause fibres to translate, agglomerate, bend, and rotate with the flow of the fibre matrix [7] - [9] . This strongly influences the rheological and mechanical properties in different parts of the final product because of the close dependence of these properties on the orientation state of the fibres. Likewise, rheological properties that are a function of the flow-induced fibre configuration in the matrix also influence the physical properties of fibre-reinforced polymer composite [8] [9] .
The effect of the interphasial zone has been already studied by Kaw and Besterfield [10] and Yeh [11] as a third constituent of the predictive models with respect to the elastic behavior of fibre-reinforced polymer composites. Gohil and Shaikh [12] and Kari et al. [13] have investigated the interphasial effect in wood-fibre-rein- forced polymer composites. It was demonstrated that the interphase, considered as a homogeneous and isotropic material, has a significant effect on the loss factor and on the prediction of the elastic properties of three phases: fibre, interphase, and polymer composite. Other works by Lamnawar and Maazouz [14] , and Larache and Agbossou [15] used theoretical and experimental approaches based on shear lag and shear modulus to show the role of the interphase in the elastic properties of composite materials. However, no studies have been found in the literature that consider these three phases in investigating the effect of the interphase on prediction of the rheological characteristics of viscoelastic pulp-fibre-reinforced thermoplastic polymer composites.
The rheological characteristics of such composites are vital to their final mechanical properties. Although natural-fibre-reinforced polymer composites and their processing have been partially reviewed in several papers, models of their rheological behavior and analysis of the rheology-processing parameter relationships have been neither investigated nor reported. This study reports on the state-of-the-art technology in the rheology of biocomposites from green-fibre polymers, including their viscoelasticity and complex rheological behaviors as influenced by different conditions. Hence, an overview of the viscoelastic properties of biomaterials derived from pulp-fibre-reinforced thermoplastic polymers is presented in order to analyze their rheological behavior as part of predicting the viscosity of polymer melts.
Giesekus proposed a constitutive model based on a concept of configuration-dependent molecular mobility [16] - [18] . In this model, the viscoelastic component of the extra stress tensor is represented with the parameters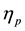 ,
,  and
and ; due to the highly nonlinear nature of the model equations, all the properties need to be obtained numerically. Moreover, this model is only able to predict low load and low shear rate in the presence of fibre.
; due to the highly nonlinear nature of the model equations, all the properties need to be obtained numerically. Moreover, this model is only able to predict low load and low shear rate in the presence of fibre.
The purpose of this study, therefore, is to present experimental and predicted results of HYP/PA11 and to validate this novel rheological modeling approach. First, we fully explored the viscoelastic-polymer-based Giesekus constitutive model. Second, we introduced the fibre and interphasial phases in function of fibre diameter and aspect ratio to the Giesekus model, considering the effect of fibre entanglement and agglomeration on the variation of the viscosity with shear rate. Finally, the model was validated by obtaining the experimental data needed to evaluate the model’s predictions.
2. Mathematical Model
2.1. Governing Equations
The equations governing the flow are the mass and momentum conservation equations.
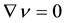 (1)
(1)
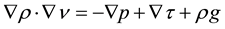 (2)
(2)
where  is the velocity vector,
is the velocity vector,  the polymer melt density,
the polymer melt density,  the polymeric extra stress contribution,
the polymeric extra stress contribution,  the pressure and
the pressure and  the gravitational velocity.
the gravitational velocity.
For polymer melts exhibiting Newtonian rheology, 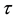 takes the form
takes the form
 (3)
(3)
where μ is the melt viscosity and  is the rate-of-strain tensor. For viscoelastic polymer melts, the stress tensor depends on the deformation history.
is the rate-of-strain tensor. For viscoelastic polymer melts, the stress tensor depends on the deformation history.
2.2. Assumptions
The model was designed on the assumption that it should describe rheological behavior as a function of the rate of deformation according to different conditions like fibre flexibility, interphasial zone and aspect ratio, and anisotropic parameter. In addition, to obtain a closed-form analytical expression for the velocity distribution as a function of the viscoelastic parameters, the following assumptions were introduced:
The flow of fibre-reinforced thermoplastic composites is assumed to be an incompressible fluid during the extrusion and injection molding processes;
The velocity field is steady and fully developed, i.e.,  ,
, ;
;
The isothermal viscosity laws are applied, i.e., the viscosity is only a function of shear rate;
The components of the composite are anisotropic, then nonlinear viscoelastic models;
The flow is in a closed system and is driven only by applying load (zero pressure gradient, i.e.,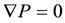 );
);
Given the high viscosity of the polymer melt, inertia is negligible.
2.3. Model Development
A single Giesekus model derived from a Maxwell element would be sufficient to model the observed relaxation- time behavior, the shear stress, and the viscosity of polymer material. However, the strong nonlinear viscoelastic expression of shear viscosity in function of high shear rate of pulp-fibre-reinforced polymer composite required the extension of the model to include more parameters. Hence, in addition to the polymer phase, the fibre and interphase phases have been formulated into the Giesekus base model.
The literature offers various concepts for modelling change in the viscous properties. It has been pointed out that only the viscous overstress and the strain rate are suitable dependencies for formulating a viscosity function.
Figure 1 shows the surface area of the flexible HYP at different points. Assuming that the fibre is flexible, when shear is applied the fibre is agglomerated at the point of diameter “D”.
The surface area of fibre before agglomeration is maximum, and is calculated as follows:
![]() (4)
(4)
At the agglomerated point, the surface area is minimum, and we obtain:
![]() (5)
(5)
![]()
Figure 1. HYP fibre of length L before load is applied: When load is applied, the fibre is entangled and agglomerated and has diameter “D”.
Assuming that the composite material has three phases and that the fibre is flexible, the total stress or the stress of the composite is represented as:
![]() (6)
(6)
The shear stress of the polymer phase:
![]() (7)
(7)
where ![]() is a model parameter attributed to anisotropic Brownian motion or anisotropic hydrodynamic drag on the constituent polymer molecules. It is required that
is a model parameter attributed to anisotropic Brownian motion or anisotropic hydrodynamic drag on the constituent polymer molecules. It is required that ![]() as discussed by Giesekus [16] - [18] .
as discussed by Giesekus [16] - [18] .
The shear stress of the fibre phase:
![]() (8)
(8)
For![]() , we have
, we have
![]() (9)
(9)
The shear stress at the interphasial phase:
![]() (10)
(10)
By rearrangement, we have
![]() (11)
(11)
Substituting Equations (7), (9) and (11) into (6) and rearranging it, we arrive at:
![]() (12)
(12)
Predicting the shear viscosity during the extrusion process and using the capillary rheometer involves a coupled analysis of flow, shear rate, aspect ratio, and interphasial effect. The resultant equation is highly nonlinear due to the viscosity, which depends on the shear rate, fibre aspect ratio, and process parameters; these nonlinearities have been solved by the Newton-Rapson method of numerical approach.
3. Materials and Methods
3.1. Materials
The matrix biopolymer bio-based Nylon 11, density 1.03, MFI 11, was supplied by Arkema, France. Aspen HYP fibers were supplied by Tembec (Montreal, QC). The HYP is the type used in wood-free printing and in writing-paper grades and multiple-coated folding-board grades; fibre length is 0.230 to 0.85 mm. Finally, the pulp-fibre length was reduced by using a mechanical crib in order to investigate the aspect ratio effect on the rheological behavior of the HYP/PA11.
3.2. Experiment
The experiment was processed using a Conical Twin Extruder. In the mixing method, the HYP fibre was dried at 80˚C for 6hours and then added to the corresponding PA11 and well mixed before it was introduced to the extruder. The average temperature of the barrel was 200˚C.
3.3. Rheological Measurements
The rheological measurements of the composites’ melt-flow properties were carried out in a twin-bore Rosand Capillary Rheometer model RH2000 (the standard RH2000 range supports temperatures from −40˚C to 500˚C. The standard maximum force applied is 12 kN). The composite samples for testing were cut into very small pieces, then placed inside the barrel and forced down into the capillary with the plunger attached to the moving cross-head. Representative steady-shear viscosity versus high shear rate is presented in the figures below for HYP/PA11, which was processed at the average extrusion temperature of 200˚C. The apparent viscosity of the sample was obtained from steady-shear measurements for different fibre aspect ratios, with the rate ranging from 50 to 5000 S−1. The rheology viscosity data presented in this paper represent an average value of three measurements.
4. Results and Discussion
The novel nonlinear viscoelastic material model was explored in order to simulate the nonlinear rheological behavior of HYP/PA11. In this study, both experimental and predictive results on HYP/PA11 were investigated in order to understand the power, validity, and capabilities of the novel rheological model developed. The detailed rheological properties are the major focus of this work.
4.1. Experimental Results
Rheological characteristics of the polymer, fibre, and interphasial phases influence the final characteristics of the resultant microstructure of composite materials; these characteristics in turn affect the mechanical properties of a multiphase polymer composite system. Experimentally, the apparent viscosity as function of the steady-shear rate of HYP/PA11 at 200˚C is shown in Figure 2 (as noted, these results are the average of three different experimental tests).
As noted, the composite material used in the experimental study had a fibre length of 0.73 mm, and the experiment was conducted at 200˚C. The experimental results showed that the apparent viscosity of HYP/PA11 composite decreases with increasing shear rate. This decrease in the shear viscosity with the increase in shear rate corresponds to the pseudoplastic fluid characteristic of the composites. This pseudoplastic behavior (also referred to as shear-thinning behavior) plotted in Figure 2 is mainly influenced by the orientation of the polymer molecules, the agglomeration of the flexible fibre, and the entanglements within the polymer chains in the capillary rheometer. Due to the flexibility of HYP, when shear is applied to the material the orientation of the fibre changes its configuration from rectangular to spherical; such modifications are produced in the fibre length and the surface area of the fibre once the orientation is completed at high shear rate. On the other hand, the chain agglomerations are produced simultaneously with collapsing one chain onto another chain. The entanglement of the chains followed by agglomerations, as well as the entanglements within the chains, are caused by the Brownian motions and low relaxation of HYP. The high shear-thinning behavior obtained for HYP/PA11 can be also associated to the thermal degradation of HYP during the rheological testing. The molten polymers tend to arrange themselves with their major axes in the direction of shear, and thereby points of entanglement are reduced.
![]()
Figure 2. Shear viscosity vs. shear rate of HYP/PA11 at 200˚C.
As a result, the viscosity decreases. In other words, in this case of non-Newtonian flow behavior of polymer melts, the decrease in viscosity when the shear rate is increased by applying load is associated with high shear- thinning behavior and with viscoelastic characteristics of biocomposite materials. However, at very high shear rates (from 3000 to 5000 S−1), the molten HYP/PA11 showed a less restrained decrease in apparent viscosity. Such high decrease in the shear viscosity is associated with high shear-thinning behavior. This non-Newtonian behavior is associated with the alignment and the orientation of the fibre in the polymer chains and the effect of the fibre aspect ratio. At low as at high shear rates, the formation of agglomerates is evident; therefore HYP molecules are completely oriented due to the good green-HYP dispersion in the bio-based PA11 matrix. This means that the breakage of the fibre length allows the maintenance of an accurate fibre-aspect ratio when the diameter of flexible HYP is kept unchangeable during the process. The shorter length of the fibres will also support their alignment in the direction of the flow, thus reducing the fibre-fibre collisions and leading to a higher decrease in the apparent viscosity.
4.2. Variation of the Viscosity with a Function of Shear Rate of HYP Reinforced PA11 at Various Temperatures
The variation of the apparent viscosity in function of the shear rate of HYP-reinforced PA11 at various temperatures was investigated and the rheological test results are presented in the Figure 3. The rheological conditions were kept constant while different tests were run for 190˚C, 200˚C, and 210˚C.
The apparent viscosity of the HYP/PA11 depended on the rate of shear at which it was measured and presented. The shearing effects decreased as the temperature increased; that is, the HYP/PA11 became more non- Newtonian in the higher temperature region. At higher temperature the reduction of the shear viscosity was more pronounced at intermediate shear rate, while for 190˚C, the reduction of the shear viscosity reached a maximum at higher shear rates (from 3000 to 5000 S−1). This characteristic is due to the fact that the HYP-reinforced PA11 fibres were agglomerated and entangled at low temperature and low and intermediate shear rate; this made flow deformation difficult (at this point this rheological behavior is called near-Newtonian). At high shear rate, the shearing effects increased while the effect of temperature was less pronounced, and flow deformation was mostly dominated by the shearing effect. However, from 3000 to 5000 S−1 all the apparent viscosity variations in function of shear rates followed the same rate of deformation for different temperature profiles; this corresponds to shear-thinning behavior.
4.3. Effect of Fibre Content on the Rheological Behavior of HYP/PA11
The effect of the fibre content on the rheological characteristics of the composite was investigated. Figure 4 shows the experimental results for 10%, 20%, and 30% HYP/PA11. These curves are typical of pseudoplastic materials, which show a decrease in viscosity with increasing shear rate. At high fibre content, the material offers higher shear viscosity even for high shear rate. In general, the incorporation of fibres in polymer systems increases the viscosity and increases further with fibre content.
The difference is not very significant for 10% and 20% fibre for intermediate and high shear rate. At low HYP content, the shear viscosity was expected to increase rapidly with increasing concentrations of the fibres because of the rapidly increasing interactions between particles as they become packed more closely to each other. Nevertheless, at very high fibre content, random anisotropic structures of fibres in the polymer melt were created. The increase in shear viscosity was found to be more predominant at lower shear rates where fibre and polymer molecules were not completely oriented.
4.4. Effect of the Fibre Aspect Ratio on the Rheological Property
The results from the study of the effect of the aspect ratio of flexible pulp-fibre-reinforced bio-based Nylon 11 are presented below in Figure 5.
At low fibre aspect ratio, the decrease in viscosity as a function of the shear rate was greater for both low and high shear rate. Contrarily, at higher fibre-aspect ratio the shear viscosity shows a moderate decrease for low and intermediate shear rate.
At low and intermediate shear rate, the viscosity curves are slightly decreased and the distance between each viscosity curve remains large. However, at high shear rate the viscosity plots are tightly close. This is because fibre agglomeration and entanglement are not pronounced at high shear rate or frequency, due to the complete
![]()
Figure 3. Variation of the viscosity with a function of shear rate of HYP/PA11 at various temperatures.
![]()
Figure 4. Shear viscosity vs. shear rate of HYP/PA11 at 200˚C.
![]()
Figure 5. Shear viscosity vs. shear rate of HYP/PA11 at 200˚C.
orientation of the fibre and polymer molecules. Much as with high fibre content, the increase in shear viscosity is found to be greater at lower shear rates, where fibre and polymer molecules are not completely oriented.
4.5. Predicted Results
In this section, the numerical plot below shows the results of the mathematical predictive model for representing the rheological characteristics of the material and the influence of processing conditions on the material’s resultant microstructure.
To verify the applicability of the formulated viscoelastic-material model, certain rheological tests were simulated and compared with the experimental data. The comparisons show that the newly developed rheological viscoelastic-material model is capable of simulating not only the dependence of shear viscosity on the material’s shear rate, but also the variation in the slope of the material’s rheological responses. The shear viscosity curve observed for HYP/PA11 is depicted in Figure 6 for 30% HYP fibre. Figure 6 shows that HYP/PA11 biocomposite acts as a pseudoplastic fluid and that the shear viscosity plots have a tendency to decrease for high shear rates. The various assumptions considered in these models, in fact, were well fitted to the fluid’s actual behavior. The fibre-agglomeration effect considered when the model was first conceived is a primary contribution to the originality of this study. Accordingly, both predicted and experimental results showed how the flexibility and entanglement of HYP fibre contributed to the change in the fibre’s total surface area and the resultant influence on the rheological characteristics of HYP/PA11 composite.
The entanglement and agglomeration of the fibre are manifested at high shear rate, where the decrease in the fibre’s surface area increases the material’s shear viscosity and consequently shows a non-Newtonian behavior. Figure 6 demonstrates that the flexibility and diameter of the pulp fibres affects the viscoelasticity of the resultant composite. Another observation is that the interphase interaction also influenced the viscosity behavior with the changing shear rate of HYP/PA11, together with the change in the aspect ratio, which was mostly present in the interphase. The interphase interaction in pseudoplastic fluid behavior is significant in the study of the shear viscosity with the increase in shear rate of high-fibre-content reinforced polymer composite. The observed decrease in the shear viscosity of composite material from the plot map of the predicted model is associated with the high degree of pseudoplasticity due to perfect dispersion of high-yield pulp fibre into the composites; this gives rise to the good reinforcing effect of HYP on PA11.
4.6. Model Validation
In this section, the comparisons between the theoretical predictions and experimental measurements are detailed. In the experiments, the shear viscosity was determined to be a function of high shear rate while polymer flow rate and processing temperature were kept constant. Experimental and predictive results from HYP/PA1 are shown in Figure 7. The average shear viscosity at the initial shear rate was about 800 Pa・s for 200˚C for low fibre aspect ratio and about 1000 Pa・s for intermediate and high fibre aspect ratio, and at this point the melt exhibited both experimentally and predictively a shift from Newton to non-Newtonian rheological characteristics. However, as the shear increased, HYP/PA11 showed highly non-Newtonian behavior, corresponding to high shear-thinning behavior. The accuracy of the predictive model derived from the experimental testing results and used for calculating the previous shear viscosity was high. Experimentally and mathematically, the shear viscosity as function of steady-shear rate of HYP/PA11 at 200˚C is shown in Figure 7 (where Exp. = experiment and M. = modeling): Ar1, Exp. Ar2, and Exp. Ar3 represent the fibre aspect ratio 1, 2, and 3; and Ar1 < Ar2 < Ar3.
Despite the discrepancy between the values for viscosity obtained by the predictive model and those from experiments from 2000 to 2500 S−1, the agreement between the model’s predictions and experimental data is remarkable given the simplicity and accuracy of the model, the exactitude of the material properties and parameters, and the fitness of the proposed boundary conditions. At both low and high shear rate, good agreement is
![]()
Figure 6. Prediction of shear viscosity vs. shear rate of HYP/PA11 at 200˚C.
![]()
Figure 7. Shear viscosity vs. shear rate of HYP/PA11 at 200˚C.
evident from the results; hence, this novel mathematical predictive rheological model is well fitted to the extrusion of viscoelastic biocomposite materials. From 3000 to 5000 shear rate both experimental and predictive results show a regular decrease on the shear viscosity, which may be due to the fact that fibre distribution and orientation are complete, and that the viscosity is mainly dependent on the mobility of the polymer chains in the composite structure. The model’s plot of shear viscosity versus shear rate is evidence that the model is applicable to mathematically representing the rheological behavior of a variety of natural fibre-reinforced thermoplastic viscoelastic composite materials.
5. Conclusion
In this study, a novel rheological model for viscoelastic materials was developed in order to predict rheological properties and then compared with experimental results on HYP/PA11. This nonlinear rheological model was developed for constant material parameters, simultaneously considering viscous, elastic, and inertial nonlinearities and interphasial phase variables and parameters. The predictive results indicated that the developed model well supports the determination of rheological characteristics of the investigated material, such as viscosity and shear stress. In addition, the rheological model was plausibly demonstrated and validated based on the experimental results of shear viscosity versus shear rate. Both experimental and predictive results showed high shear- thinning behavior on HYP/PA11 associated with a high degree of pseudoplasticity due to the good dispersion of HYP into PA11 and the orientation of the flexible fibre effects in the direction of the molten PA11. The model was validated for different fibre aspect ratios and high shear rate, up to 5000 S−1. Due to its consistency and its high predictive ability, the model may be applied in rheological studies and investigations of viscoelastic materials, particularly in the automobile, construction, and aerospace industries.
Acknowledgements
This work was carried out with the support of Mitacs funding; the University of Toronto and the Ford Motor Company financially supported this study.
NOTES
*Corresponding author.