Possible Magnetic Resonance Signal Due to the Movement of Counterions around a Polyelectrolyte with Rotational Symmetry ()
1. Introduction
Polyelectrolytes are ionizing macromolecules. An important property of polyelectrolyte molecules is the forma- tion of electric double layers surrounding the polymer chains. Most of the biological macromolecules under physiological conditions are polyelectrolytes in solution and their biological activity depends on their physico-chemical properties. Depending on the strength of the electrostatic interactions, it has been found [1] that distinct “phases” of counterions can be formed, i.e., a “condensed” layer of mobile oppositely charged counterions [2] [3] and “diffuse” phase consisting of loosely bound counterions to the considered macroion. The last phase of collective motion of the more mobile ions can be involved in the formation of charge density waves.
Experimental [4] - [7] , theoretical [8] - [14] and computational [15] - [17] studies reveal that the characteristic time scales involved in counterion dynamics in polyelectrolyte systems may span several orders of magnitude ranging from subnanosecond times to time scales corresponding to acoustic frequencies. The counterions exhibit an acoustic-like phonon mode that suggests the existence of a correlated phase. At small length scales within the domains, counterions exhibit liquid-like correlations and dynamics, and they are organized into counterion charge density waves (CDWs) [18] . The measured speed of sound is of the order of 2000 m/s.
We believe that these CDWs exist also on the surface of polyelectrolytes with rotational symmetry generating a circular current loop, which produces a magnetic field  and the corresponding magnetic moment
and the corresponding magnetic moment 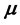 at the center of the macroion. This magnetic moment
at the center of the macroion. This magnetic moment  is oriented in an external magnetic field
is oriented in an external magnetic field 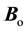 producing a magnetic resonance signal under the aplication of a certain frequency
producing a magnetic resonance signal under the aplication of a certain frequency .
.
2. Magnetic Field on the Axis of a Circular Current Loop
Consider a circular loop of wire of radius 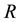 located in the xy plane and carrying a steady current
located in the xy plane and carrying a steady current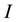 , as shown in Figure 1. The magnetic field at an axial point P a distance
, as shown in Figure 1. The magnetic field at an axial point P a distance 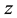 from the center of the loop is given by [19] :
from the center of the loop is given by [19] :
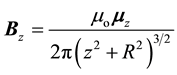 (1)
(1)
where 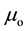 is the permeability of free space,
is the permeability of free space,  and
and  is the magnetic moment associated with the current loop, where
is the magnetic moment associated with the current loop, where 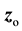 is a unit vector in the
is a unit vector in the  direction. The magnetic field at the center of the loop, we set
direction. The magnetic field at the center of the loop, we set ![]() in Equation (1). At this special point, this gives1,
in Equation (1). At this special point, this gives1,
![]() (2)
(2)
In case that the current loop is produced by charged particles in movement, with electric charge q and velocity![]() . The magnetic moment is given by,
. The magnetic moment is given by,
![]() (3)
(3)
where we have used![]() , with
, with![]() , with
, with ![]() the period and
the period and ![]() the angular and linear velocity
the angular and linear velocity
of the counterions respectively.
3. Magnetic Resonance
A magnetic moment in a external magnetic field ![]() adquires an energy E given by the following escalar
adquires an energy E given by the following escalar
![]()
Figure 1. Magnetic field on the axis of a circular current loop.
product [20] ,
![]() (4)
(4)
We observe that the highest and lowest energy is when ![]() and
and ![]() this means that when
this means that when ![]() and
and ![]() are in opossite directions the energy is maximum and in the same directions is minimum. This last state is the most natural tendency of the magnetic dipole, paralell to the field. The difference in energy between this two states is given,
are in opossite directions the energy is maximum and in the same directions is minimum. This last state is the most natural tendency of the magnetic dipole, paralell to the field. The difference in energy between this two states is given,
![]() (5)
(5)
Reemplacing ![]() given by Equation (3) in Equation (5), considering
given by Equation (3) in Equation (5), considering![]() ,
, ![]() being the valence of the ions and
being the valence of the ions and ![]() , the elementary charge, we obtain,
, the elementary charge, we obtain,
![]() (6)
(6)
As an example consider the circular movement of counterions on the surface of a polyelectrolyte, used in nanomedicine with rotational symmetry, as shown in Figure 2, this does not mean that this effect can be visualize necessarily in this molecule. These ions with charge ![]() and velocity
and velocity ![]() produce a magnetic field
produce a magnetic field ![]() and a magnetic moment
and a magnetic moment ![]() perpendicular to the plane of the macroion in accordance to Equation (2) and Equation (3). If we put this magnetic moment in an external magnetic field
perpendicular to the plane of the macroion in accordance to Equation (2) and Equation (3). If we put this magnetic moment in an external magnetic field![]() , its orientation will no longer be random. The small magnetic moment may spontaneously “flip” from the most favorable orientation, the low- energy state and the less favorable orientation the high-energy state and visceversa. The energy required to induce flipping and obtain a Magnetic Resonance (MR) signal, given by Equation (6), is shown in Figure 3 to depend on the strength of the magnetic field
, its orientation will no longer be random. The small magnetic moment may spontaneously “flip” from the most favorable orientation, the low- energy state and the less favorable orientation the high-energy state and visceversa. The energy required to induce flipping and obtain a Magnetic Resonance (MR) signal, given by Equation (6), is shown in Figure 3 to depend on the strength of the magnetic field ![]() in which the macroion containing the magnetic moment is placed. The input radiation energy in order to accomplish the transition given by Equation (6) is given by Planck’s law
in which the macroion containing the magnetic moment is placed. The input radiation energy in order to accomplish the transition given by Equation (6) is given by Planck’s law
![]() (7)
(7)
Using Equation (6), we obtain for the resonance frequency,
![]() (8)
(8)
where ![]() is Planck’s constant
is Planck’s constant![]() .
.
4. Conclusions
The distribution of molecular magnets in the different energy states is given by the Boltzmann equation,
![]() (9)
(9)
![]()
Figure 2. G3 PAMAM dendrimer surrounded by counterions with velocity V.
where ![]() and
and ![]() represent the population of molecular magnetic moments in upper and lower energy states, respectively.
represent the population of molecular magnetic moments in upper and lower energy states, respectively. ![]() is Boltzmann constant and T is the absolute temperature (K). To give some idea of the consequences of increasing magnetic field on the population of molecular magnets states, the distribution of a small number (about two million, non real2) of macroions magnets, calculated from Equ- ation (9), is shown in Figure 3.
is Boltzmann constant and T is the absolute temperature (K). To give some idea of the consequences of increasing magnetic field on the population of molecular magnets states, the distribution of a small number (about two million, non real2) of macroions magnets, calculated from Equ- ation (9), is shown in Figure 3.
Such a small population difference presents a significant sensitivity problem for MR because only the dif- ference in population is detected; the others effectively cancel one another. As seen from Equation (8) and Equation (9), the use of stronger magnetic fields will increase the population ratio, and consequently the sen- sitivity. In Table 1, we observe that the resonance energy, varies between ![]() units and the resonance frequency between
units and the resonance frequency between ![]() while the magnetic field varies between
while the magnetic field varies between![]() , for a polyelectrolyte 10 nm radius with
, for a polyelectrolyte 10 nm radius with ![]() and
and![]() .
.
In Table 2 are reported NMR energy and frequency data of 3 nuclei. Compared with Table 1 for the counterions, we observe that the NMR values are one to three digits lower.
In case that this signal is detected in macroions or other biological systems, like micelles, vesicles, organeles, etc. with rotational symmetry, this method opens a new tool to measure with precission the counterions velocity.
![]()
Figure 3. Dependence on magnetic field strength Bo of ΔE and the relative popu- lations of the energy levels for counterions with z = 2 and velocity V = 2000 m/s and a macroion with R = 10 nm.
![]()
Table 1. Results shown in Figure 3.
The magnetic moment for phonons counterions with velocities of the order of 2500 m/s and for a macroion of 10 nm radius with ![]() is
is![]() , of the order of Bohr magneton
, of the order of Bohr magneton ![]()
NOTES
1The SI unit of magnetic field is the tesla (T):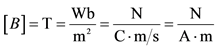 . In practise, the cgs unit for magnetic field, called the gauss (G) 1 T = 104 G.
. In practise, the cgs unit for magnetic field, called the gauss (G) 1 T = 104 G.
2In practice we put a huge number (approaching Avogadro’s number) of molecular magnets in the sample that is placed in a magnetic field.