1. Introduction
There are a variety of individual bodies on the division of work. This paper would consider the invisible body- balancing network and economics by a medium approach. This medium approach originated from a Newsboy problem [1] , and would be attained by the invisible hand of market (demand) speed.
The traditional balancing problem originates from Ford system, and is essential to the economy of mass production (economics) in the automobile industry [2] . This problem is dependent on the demand and supply speed (cycle time) in the market, and relates to the conveyor speed vs. efficiency (cycle time) in the assembly line.
The related domain is called the line balancing in Industrial Engineering (IE), and is based on the principle of system balancing in the assembly industry, including service types [3] . This solution method tends to pursue the mean inventory in the factory toward the lean inventory on the line speed in the demand-to-supply system (SCM).
In the Toyota system [4] , the line speed is determined and balanced by the demand speed in the market, and Kanban system gives a solution method of the efficiency vs. muda (loss) in the demand and supply system of pull type. However, this solution tool is an improvement approach to lean inventory.
We here consider the medium approach to the efficiency vs. muda (loss) problem in the stochastic system balancing, based on the medium inventory that originates from the Newsboy in Operations Research (OR). This paper would be prepared to apply this approach to the SCM/GDP system in the country-like region toward the near future.
2. Body-Balancing System
2.1. Economics in Balancing Problem
Modern society is being formed by the worldwide division of work as we move towards globalization. Since 1776, there is the problem of invisible hand by Smith [5] , and this problem become more important at global economics. At the classics, the price is central (Smith), and the production quantity is at next considered as the newer actor (Keynes [6] ). Recently, it is pointed out in Matsui [7] that the demand speed would be near to the invisible hand, because it would bring each maximal-profit (re-) balancing in the changeable market economy.
Generally, the body-centered network (SCM/GDP) might be able to be invisibly balanced and cooperated by the demand speed (God hand) and cloud computing [8] . However, there is the profit-balancing at series’ types, otherwise may the cost-relative balancing at parallel types [9] . Thus, this God-like hand would be alive and the win-win would be attainable at not only SCM networks but also Smith’s world only under equally partnership.
As an example, let us consider the two- or three-center model consisting of sales, assembly and fabrication centers [10] . The two main types of configuration are series and parallel systems. The SCM is a series type, and ERP (enterprise resource planning) is a parallel type. For a series class, the profit maximization is attainable under the demand speed given (shared), even if each heterogeneous agent (enterprises) pursues the self-goal in non-cooperation under indivisible environment.
Thus, each unit-optimization in profit gives the total optimization in sum under non-cooperation, and the point (balancing) occurs at near middle lead-time (reliability). This class is called the integral optimization, and might be governed by the Ellipse map and strategy in Matsui [11] .
Our profit is corresponded to the marginal profit/value in Accounting/GDP, and it is similar to the medium criterion in [12] . In the classics, A. Smith presents the first concept on the invisible hand in 1759 [13] , prior to 1776. This concept might be near to that of medium criterion in our balancing issues.
2.2. Medium Balancing Approach
The stochastic balancing problem is a class of the Conveyor-Serviced Production Station (CSPS) and its networks [14] . This study is called the station-centered approach to the power-conveyor system, and this station is here corresponded to the individual bodies (human, house, enterprise, etc.) in the society or country.
In the body balancing system, the definition of stochastic balancing is here as follows: A stabling phenomenon of transient, bottlenecked vs. balanced, state of the object system. The balanced solution by this stochastic balancing becomes quasi-optimal.
Recently, the medium approach to the body-balancing system is outlined to SCM type in Figure 1 [12] . In Figure 1, 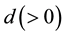 is the demand speed (cycle time), and also,
is the demand speed (cycle time), and also, 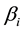 and
and 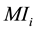 are the medium criterion
are the medium criterion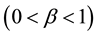 , and moving-standard inventory in the individual body,
, and moving-standard inventory in the individual body, 
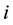 , respectively.
, respectively.
The medium criterion, 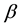 , is controlled by
, is controlled by , in which the parameters
, in which the parameters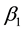 ,
,  and
and
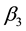 are the cost coefficients (penalties) of inventory holdings, excess inventory and shortage inventory, respectively.
are the cost coefficients (penalties) of inventory holdings, excess inventory and shortage inventory, respectively.
Now, the Newsvendor’s condition [1] is the followings:
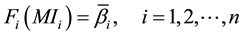 (1)
(1)
where 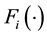 is the distribution function of the inventory in the in the individual body,
is the distribution function of the inventory in the in the individual body, .
.
Then, the balancing goal is given by the following objective function:
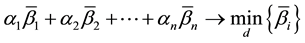 (2)
(2)
where  is the weight factor
is the weight factor![]() ,
,![]() .
.
![]()
Figure 1. A body-balancing system of a supply chain (economics) in [7] .
An optimal condition (balancing) is assumed from the classical inequality and Matsui’s equation ![]() [12] as follows:
[12] as follows:
![]() (3)
(3)
In (3), ![]() and
and ![]() correspond to
correspond to ![]() and
and![]() , respectively, and
, respectively, and ![]() means a balancing value at the equilibrium.
means a balancing value at the equilibrium.
3. Two Balancing Principles
3.1. d-Balancing Principle
Two principles on the medium balancing are here presented and considered. At first, the ![]() -balancing problem (2) is seen on the upper level of 2-level scheme in Figure 1. This main problem is easily decomposed of the dual problem:
-balancing problem (2) is seen on the upper level of 2-level scheme in Figure 1. This main problem is easily decomposed of the dual problem:
![]() (4)
(4)
in the respective body of entity![]() . Matsui’s point,
. Matsui’s point, ![]() , is based on the so-called Chameleon’s criteria [12] .
, is based on the so-called Chameleon’s criteria [12] .
Now, the following condition is considered under the demand speed (cycle time), ![]()
![]() , and the exponential service with the mean,
, and the exponential service with the mean, ![]() (supply speed). That is,
(supply speed). That is,
![]() (5)
(5)
and the demand speed, ![]() , is as follows:
, is as follows:
![]() (6)
(6)
On d-balancing, the following relation is obtained from (6):
![]() (7)
(7)
Especially, for Poisson service, the optimal condition is
![]() (8)
(8)
where ![]() is Poissonian type distribution.
is Poissonian type distribution.
These relations are outlined in Figure 2. From Figure 2 and Matsui’s equation [12] , the balance equation is
![]() (9)
(9)
and the balancing principle is
![]() (10)
(10)
from (9) and the classic inequality.
![]()
Figure 2. Outline of rebalancing problem and Matsui’s equation![]() .
.
3.2. Network Flow Principle
On the lower level, the entity ![]() is state of the body
is state of the body ![]() and period
and period![]() , and the network flow
, and the network flow ![]() is seen in Figure 3. This network flow would be behaviored under demand speed,
is seen in Figure 3. This network flow would be behaviored under demand speed, ![]() , in the body-centered balancing.
, in the body-centered balancing.
Now, the following notations are introduced in each ![]() and
and ![]() from [14] :
from [14] :
![]() : Order scheduled for body
: Order scheduled for body ![]() and period
and period![]() ;
;
![]() : Expected demand in body
: Expected demand in body ![]() and period
and period![]() ;
;
![]() : Next inventory at the end of body
: Next inventory at the end of body ![]() and period
and period ![]()
![]() .
.
where ![]() is the backorder position (quantity).
is the backorder position (quantity).
For each![]() , the balance relation on demand and supply is from Figure 3 and [15] as follows:
, the balance relation on demand and supply is from Figure 3 and [15] as follows:
![]() (11)
(11)
From (11), the second balancing principle is obtained as follows:
![]() (12)
(12)
where the second and third terms of right hand are corresponded to the coordinating of the moving marginal inventory, ![]() , and end inventory,
, and end inventory, ![]() , at
, at![]() , respectively.
, respectively.
The equation (11) is similar to that of progressive control in [12] . Thus, our network flow is governed under ![]() -balancing by the order quantity,
-balancing by the order quantity, ![]() , in (11).
, in (11).
4. Case of d-Balancing
4.1. Conveyor System with Stopper
The usual conveyor systems are the two types of the stations with or without stopper. These systems are treated in [11] by a stochastic approach. This stochastic treatment aids at the minimization of the irregular interruption in delay and idleness at the series type.
A cost approach to the delay and idleness is seen in [11] , and this balancing problem is considered by the 2- stage method. An example of stopper type is seen in Figure 4, the cycle time is 1.5 minutes, and the number of stations is![]() .
.
The Newsboy method to this case [16] gives the penalty cost function as follows:
![]() (13)
(13)
where the right hand consists of the objective of -th station:
![]() (14)
(14)
![]()
Figure 3. SCM/GDP-economic system: A network flow representation with backorder.
![]()
Figure 4. Pitch diagram and buffers: another verification.
in which ![]() is the p.d.f. of work time at the
is the p.d.f. of work time at the ![]() -th station.
-th station.
Then, the optimal condition is obtained by a differenciation method in the followings:
![]() (15)
(15)
The cycle time, ![]() , is determined by the Equation (14), and this equation is here available in replace of (2).
, is determined by the Equation (14), and this equation is here available in replace of (2).
For example, let us![]() ,
, ![]() and
and![]() . From (15), the optimal cycle time,
. From (15), the optimal cycle time, ![]() , is given by
, is given by ![]() for the Erlangian with phase
for the Erlangian with phase ![]() in the work time of stations.
in the work time of stations.
4.2. Two Balancing Views
Now, let us apply the simulator of SALPS soft [12] to this case. The simulation result is seen in Table 1, and the optimal cycle time, ![]() , is
, is ![]() with a slight difference. In addition, the total cost would be negligible.
with a slight difference. In addition, the total cost would be negligible.
Another verification is considered by Figure 5. From Figure 5, the bottleneck of the system is seen in the stations, 2 ![]() and 5
and 5![]() , in Table 1. The balancing hypothesis in (3) would be valid.
, in Table 1. The balancing hypothesis in (3) would be valid.
![]()
Figure 5. A two-stage supply chain system for balancing.
![]()
Table 1. An verification of medium balancing: simulation trial case.
5. Case of Network Flow
5.1. A Two-Stage Supply Chain
Next, let us consider the two-stage supply chain (SCM) of a franchise type in Figure 5. This case consists of a series of factory, ![]() , and warehouse,
, and warehouse, ![]() , and is seen in Figure 5 [16] .
, and is seen in Figure 5 [16] .
In the case, the outflow is uncontrollable, and the system is only controllable by inflow.
For this case, the balancing problem is the minimization of the total inventory between suppliers. That is,
![]() (16)
(16)
The objective (16) is here available in replace of (2).
5.2. A SCM Simulation Practice
For this case, the ![]() balancing table is presented and considered on the network flow balancing. The total inventory in one year is 5176, and is improved much more than the practice (8074).
balancing table is presented and considered on the network flow balancing. The total inventory in one year is 5176, and is improved much more than the practice (8074).
From Table 2, the medium balancing holds except July, September and April as follows:
![]() (17)
(17)
It is them noted that any bottleneck phenomena would be doubtful in July, September and April.
This result would show the effectiveness of medium balancing method, and the hypothesis (3) is ascertained.
6. Conclusions
This paper summarizes a recent approach (possibility) to the medium (Chameleon’s) balancing from conveyor system toward SCM/GDP-economic system. First, the body-balancing problem was briefly outlined. Next, the unified economics treatment to the physical balancing problem was presented.
Finally, an optimal condition of balancing was pointed out and verified at the view of Matsui’s equation and Chameleon’s criteria. The materials would give a shortcut way to the traditional balancing method, for example, much more than the 2-stage method [11] . By the paper, the concept of balancing is utilized in physics and economics, and is extended to the science of discrete world.
By the further study, the GDP balancing of the country would become probably possible on the base of pro-
gressive and autonomous control of marginal profit/value in GDP networks. This foundation may be derived by changing from the invisible hand to visibility of demand-to-supply speed.