Mode Recognition of Lamb Wave Detecting Signals in Metal Plate Using the Hilbert-Huang Transform Method ()
1. Introduction
Lamb waves (LW) are special form of stress waves composited by longitudinal and transverse waves in the sheet metal, and the wave length of LW is at the same order of magnitude with the thickness of the sheet metal [1] . At the given excitation frequency, there are at least two modes of LW and the dispersion phenomenon exists in each mode. Besides, the phase velocity of each mode varies with the change of excitation frequency [2] . The Rayleigh-Lamb equations describe the wave characteristic and represent the physical properties such as multi- mode and dispersion [3] . The multi-mode and dispersion characteristics make the LW complex to be excited, transmitted, interaction with defects, received and processed, and this confines its widespread use in the industrial manufacture.
Analyzing the LW signals that can reflect the defects received by the detector is an important content in detecting metal defects based on LW. The level of explaining received signals has the direct bearing on the evaluation of the defects properties in the detected sheet metal. Due to the unique characteristics of multi-mode and dispersion, when all modes of LW overlap each other and form wave packets, it will be difficult to analyze and explain the detected signals because it’s hard to distinguish the multi-modes in the propagation time domain.
LW detecting signals are typical non-stationary signals [4] . Some scholars have applied the time-frequency method to recognize different LW modes, but the results show varying degrees of limitations. The wavelet transform (WT) is used in Hinders’ work to extract LW signal characteristics interacting with defects, and these statics are then fed to statistical pattern classification algorithms that identify flaw severity [5] . Researchers at the University of Sydney use WT and artificial neural network algorithms for mode recognition in CF/EP composite structures [6] . The short-time Fourier transform (STFT) is used to estimate the propagation mode of LW in aluminum alloy plate in the work of TengFei, but the spectral analysis and flight time extraction results are not accurate enough, leaving negative influence on the estimation [7] . Zhang Haiyan uses Hilbert-Huang transform (HHT) to extract flight time in LW tomography, but only for the direct waves, neither the boundary nor defects reflected waves are analyzed [8] . Jidong Hou uses a dynamic wavelet fingerprint (DWFP) to automatically detect and evaluate each candidate through-transmitted Lamb mode [9] . In Ma Ding’s work, the piezoelectric wafer active sensor (PWAS) is used to detect an aluminum plate, and the empirical mode decomposition (EMD) method and WT are used to separate the LW packets. But the damages are simulated, so the results show less practical value [10] . HHT is applied in Quek’s work as a signal processing tool to locate an anomaly, with the method of sorting flight times, while the HHT’s advantage of separating different modes is hardly shown [11] . With piezoelectric sheets as actuators and receivers in Byungseok’s work, HHT is used to evaluate structural damage in the curved composite panel [12] . Some of these works depend on simulated LW signals without the foundation of actual LW signals, while others only analyze the direct LW signals without any boundary or defect reflection.
There is still important significance to analyze the boundary reflected LW signals, because for thorough hole defects, the reflected LW are similar with that of boundary, with only smaller signal amplitude; and for other types of defects, the detection is still based on reflection. Therefore, analyzing boundary reflected signals can provide important reference for the analysis of defects reflection signals. The experimental LW detecting system for single aluminum plate will be setup in this work, and HHT will be used to recognize overlapped LW detecting signals of different modes, including direct waves and boundary reflected waves.
2. LW Dispersion and Multi-Mode Characteristics
Rayleigh-Lamb equations directly determine the dispersion and multi-mode characteristics of LW. The wavenumber and angular frequency of LW propagating in the metal plate are in non-linear relationship, and the relationship also varies in different wave modes. Therefore, the phase velocity of each mode varies with its frequency and this characteristic is called dispersion of LW, and this phenomenon can be reflected by the LW phase velocity dispersion curve. The mode recognition refers to recognizing the specific mode of the propagating LW by analyzing the detected signals and comparing with the theoretical dispersion curve [13] . The research object of this paper is the 3 mm thick aluminum plate with 6300 m/s longitudinal wave velocity and 3300 m/s transverse wave velocity. Figure 1 shows the group velocity dispersion curves of LW propagating in this aluminum plate based on calculation and the excitation frequency of the working point is 83 kHz.
3. Basic Theory of Hilbert-Huang Transform (HHT)
HHT is firstly proposed by Huang N E at NASA in 1998. There are mainly two steps: 1) the signal is decomposed into several intrinsic mode functions (IMFs) by the method of EMD; 2) performing Hilbert transform (HT) on IMFs. The most important feature of HHT is that the composition relies on no particular function, and each IMF can be seen as one of the vibration modes in the signal, which can express its local characteristics [14] .
![]()
Figure 1. The group velocity dispersion curves of LW propagating in 3 mm thick aluminum plate.
3.1. Empirical Mode Decomposition (EMD)
A function is said to be IMF if it satisfies the following two conditions: 1) in the whole data set, the number of extrema and the number of zero crossings must either equal or differ at most by one; 2) at any point, the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zero. The decomposition process is to divide the signal into its family of intrinsic modes. Based on the IMF definition, the decomposition process can use the envelopes defined by the local maxima and minima separately. All the local maxima can be connected by a cubic spline function to define the upper envelope curve, and the lower envelope curve can be produced by the similar way.
The mean of upper and lower extrema curves is designated as
 (1)
(1)
Xmax: the local maxima of the signal; Xmin: the local minimal of the signal; Xm1: the mean of upper and lower extrema curves.
The first estimation of an IMF is
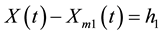 (2)
(2)
X: the original signal; h1: the first estimation of an IMF.
This process is called sifting. The next sifting process assumes that h1 becomes the signal and the next estimation is
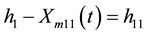 (3)
(3)
Xm11: the mean of upper and lower extrema curves of h1; h11: the next estimation of IMF.
Further sifting is usually needed and by performing k successive siftings a better estimation of the first IMF can be obtained as
 (4)
(4)
c1: the obtained first IMF.
The standard deviation between two successive siftings to terminate the sifting process is
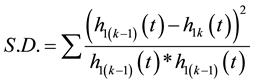 (5)
(5)
The residual signal can be computed as
 (6)
(6)
The residual then acts as the new data to extract more IMFs. And the process repeats to obtain c2 through cn. The original signal can be represented by summing up all the IMFs and the last residual as
 (7)
(7)
Therefore, the original signal is divided into several IMFs [15] .
After the sifting process, components of different vibration modes can be separated from each other, while it’s hard to separate components of the same vibration mode.
3.2. Hilbert Transform (HT)
The second process is performing the Hilbert Transform (HT) on the IMFs. For the given IMF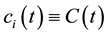 , the HT is
, the HT is
 (8)
(8)
Then the analytic signal becomes
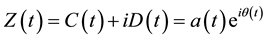 (9)
(9)
The amplitude and phase above are defined as
 (10)
(10)
a(t): the amplitude of Z(t); θ(t): the phase of Z(t).
According to the expressions of HT, better time characteristic can be obtained by HT compared to original signal, which can extract the time component more accurately.
4. Setup of the Experimental LW Detecting System for Aluminum Plate
The electromagnetic acoustic transducer (EMAT) is built with a close winding spiral coil and a permanent magnet. Figure 2 shows the structure and schematic diagram of the EMAT. Because the coil is in ring, the generated LW will propagate to all directions.
The 100 cm × 100 cm, 3 mm thick aluminum plate is used in this experiment. Figure 3 shows the area size of the plate and the positions of transducers. The above-mentioned EMATs is used to generate and receive LW, and the distance between the two EMATs is 90 cm. Figure 3 also shows possible propagation paths of LW in the plate. As shown in Figure 3, #1 is the direct wave, #2 is the boundary reflected wave and #3 is the opposite boundary reflected wave. Because the transducers are omni-directional, the excited LW propagate along the aluminum plate and when run into the opposite boundary, it will reflect and be received by the receiver.
Figure 4 shows the schematic diagrams of the experimental system. The transmitter is excited by a RF power amplifier (AG1024) that is controlled by a personal computer (PC). The peak-to-peak amplitude of the tone- burst pulse excitation voltage is 300 V, the excitation frequency is 83 kHz and the periodicity is 7. The detected signals are filtered and amplified by a signal conditional circuit and subsequently collected by a high-speed DAQ card. Finally, the collected inspection data are sent to the PC to be calculated and analyzed.
The signal waveform collected by the DAQ card is shown in Figure 5.
According to the group velocity dispersion curves in the aluminum plate shown in Figure 1, two modes of LW S0 and A0 will be excited in the 3 mm thick aluminum plate at the excitation frequency of 83 kHz, and the theoretical velocities are 5382 m/s and 2482 m/s, respectively. In Figure 5, wave a is the pulse wave form space induction, wave b, c and d are LW propagating in the aluminum plate received by the receiver. On the basis of transducers’ positions and the size of the aluminum plate, in the time range being acquired, the possible LW are: the direct wave in S0 mode #1(S0), the direct wave in A0 mode #1(A0), the boundary reflected wave in S0 mode #2(S0), the boundary reflected wave in A0 mode #2(A0) and the opposite boundary reflected wave in S0 mode #3(S0). According to their propagation distances and theoretical velocities, their theoretical propagation
![]()
Figure 2. The structure and schematic diagram of the EMAT.
![]()
Figure 3. Positions of the EMATs and possible propagation paths of Lamb waves.
![]()
Figure 4. The schematic diagrams of the experimental system.
![]()
Figure 5. Signal waveform collected by the DAQ card.
time is shown in Table 1.
In Figure 5, the actual propagation time of wave d is 470 μs, and the theoretical propagation time of #2(A0) in Table 1 is 443 μs, so their relative error is 6%. Therefore, wave d is the boundary reflected wave in A0 mode #2(A0). According to the actual flight time of wave b and wave c in Figure 5 and their theoretical propagation time in Table 1, #1(S0) and #2(S0) overlap each other to form wave b in the time domain, and #1(A0) and #3(S0) overlap each other to form wave c in the time domain. Because their propagation time is close to each other, they can hardly be recognized in the time domain. In the consideration of HHT, it will be used to analyze and recognize these overlapped waves.
5. LW Detecting Signals Analysis by HHT
In order to eliminate possible interference to make the analysis more accurate, only wave b, c and d are analyzed, excluding the influence of space inducted pulse a, which occupies the time scale of 133 μs. The signal waveform being analyzed is shown in Figure 6, and the time component can be the actual propagation time as long as being added with 133 μs.
The EMD method is used to decompose the signals in Figure 6. Totally six IMFs and one residual are obtained. The amplitudes significantly decrease after the third IMF, so the later IMFs have little influence on the properties of the original signal. The first three IMFs are shown in Figure 7.
In the waveform of IMF1, it can be clearly seen that two modes of signals are decomposed from wave c in Figure 6. Besides, the amplitude of IMF1 is close to that of the original signal, so it can better reflect the original characteristics. Then HT is used to analyze IMF1 and Figure 8 shows the result.
It’s more clear that after HT, the wave c is indeed decomposed into two components, whose time component are 226 μs and 279 μs, respectively. After being added with 133 μs, their actual propagation time is 359 μs and 412 μs, respectively. The comparison with the theoretical propagation time of #1(A0) and #3(S0) is shown in Table 2.
![]()
Table 1. Possible waves and their theoretical propagation time.
![]()
Table 2. Comparison on the theoretical and actual propagation time of #1(A0) and #3(S0).
![]()
Figure 6. The time domain waveform of the signal being analyzed.
Table 2 indicates that the time extracted from IMF1 after HT is very close to the theoretical propagation time of #1(A0) and #3(S0), and their errors are small, which verifies the previous supposes. The overlapped #1(A0) and #3(S0) are successfully separated by the EMD method and the flight time are accurately extracted by HT. Therefore, the mode recognition of LW detecting signals in aluminum plate is achieved.
In previous supposes, wave b should contain #1(S0) and #2(S0) of the same LW mode, but the results show that they are not separated by EMD. This also agrees with the EMD theory that it’s hard to separate signal components of the same vibration mode.
6. Conclusion
The EMD algorithm and HT theory are introduced and analyzed in this work, and the experimental LW detecting system for single aluminum plate is setup. The LW detecting signals (including direct waves and boundary reflected waves) are analyzed by HHT and the overlapped LW signals are recognized. Results show that EMD can clearly separate overlapped LW detecting signals of different modes and HT can extract accurate flight time in IMF, but EMD could hardly recognize LW signals of the same mode, agreeing with the theoretical analysis. Therefore, HHT can be an effective method to recognize LW detecting signals of different modes in metal plates.
Acknowledgements
This research was supported by the National High Technology Research and Development Program of China (863 Program) (No. 2011AA090301), by the National Natural Science Foundation of China (No. 51107058) and by the Tsinghua University Initiative Scientific Research Program (20111080983).
NOTES
*Corresponding author.