A Note on the Structure of Affine Subspaces of L²(R^d)

Fengying Zhou^*, Xiaoyong Xu

School of Science, East China Institute of Technology, Nanchang, China.

DOI: 10.4236/apm.2015.52008                

Abstract

This paper investigates the structure of general affine subspaces of L²(R^d) . For a d × d expansive matrix A, it shows that every affine subspace can be decomposed as an orthogonal sum of spaces each of which is generated by dilating some shift invariant space in this affine subspace, and every non-zero and non-reducing affine subspace is the orthogonal direct sum of a reducing subspace and a purely non-reducing subspace, and every affine subspace is the orthogonal direct sum of at most three purely non-reducing subspaces when |detA| = 2.

Keywords

Affine Subspace, Reducing Subspace, Shift Invariant Subspace, Orthogonal Sum

1. Introduction

Let A be a d × d expansive matrix. Define the dilation operator D and the shift operator T_k, , by

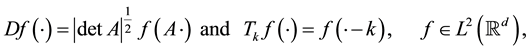
respectively. It is easy to check that they are both unitary operators on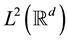. Given a closed subspace X of, X is called a shift invariant subspace if 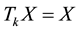for every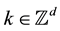; X is called a reducing subspace of 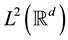if and for every; X is called an affine subspace of if there exists an at most countable subset 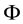of such that

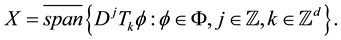
In this case, we say that generates the affine subspace X. An affine subspace, which does not contain any non-zero reducing subspace, is called purely non-reducing. By Theorem 3.1 in [1] , a closed subspace X of

is an affine subspace if and only if for some shift invariant subspace

M. Therefore an affine subspace X of is a reducing subspace if and only if it is shift invariant. So far, the study of reducing subspaces has achieved fruitful results. The existence and construction of wavelet frames for an arbitrary reducing subspace can be seen in [2] -[7] . For one-dimensional case A = 2, Gu and Han investigated the existence of Parseval wavelet frames for singly generated affine subspaces in [8] and the structural properties of affine subspaces in [9] . For a given d × d expansive matrix A, Zhou and Li studied the construction of wavelet frames in the setting of finitely generated affine subspaces of in [10] . For a general d × d expansive matrix A, this paper focuses on the structure of affine subspaces of, which is a continuation of the literature [10] and has not been investigated yet.

2. Main Results

Lemma 1. Let X and Y be closed subspaces of a Hilbert space H and be the orthogonal projection onto. Then

1)

2)

Proof. 1) Obviously,. For the other direction, note that

then

So. Therefore,. Thus 1) holds.

2) For, there exists some such that. So , or, which shows due to the fact that. For, we have and. Thus for any, there is g with and and such that. Consequently,

since. The proof is completed.

Lemma 2. Let be a monotone sequence of subspaces in a Hilbert space.

1) If is increasing, then

2) If is decreasing, then

Proof. We only prove 1) since 2) can be obtained similarly. Since is increasing, the first equality is obvious and

If, then for any, there exists, and such that and. For such h, there is a unique sequence and a unique such that for each, and. This means that

The proof is completed.

Proposition 1. Suppose that X is an affine subspace of with M being its generating shift invariant subspace. Then there exist a shift invariant subspace M₁ in X and a reducing subspace Y of contained

in X such that the length of M₁ is no more than that of M and.

Proof. For each, define

Obviously, for and. Let. Similarly to the proof of Proposition 2.2 in

[10] , we know that Y is a reducing subspace. Now define. Then by Lemma 2 and

Suppose that for some subset such that

Since is a shift invariant subspace, so is. Thus for each,. Also note that. Therefore, by Lemma 1,

which shows that M₁ is a shift invariant subspace of length no more than the length of M. The proof is completed.

Proposition 2. Suppose that X is a non-zero affine subspace of and Q is the maximal shift invariant subspace contained in X. Then the following hold:

1) and is a shift invariant subspace contained in X;

2) if and only if X is purely non-reducing subspace of.

Proof. 1): Obviously, is shift invariant space since Q is shift invariant. So due to the fact that Q is the maximal shift invariant subspace contained in X. Thus is a shift invariant subspace contained in X.

2): By 1) and Lemma 2, it follows that

If X is purely non-reducing, then since is a reducing subspace. So. Suppose and X contains a reducing subspace Y. Next we only need to show. Since Y is reducing, we have and, i.e.,. Also note that

. Hence. Thus for each,. Therefore, which shows that. The proof is completed.

Proposition 3. Let X be an affine subspace of, and define. The is the maximal shift invariant subspace contained in X.

Proof. We first show that is shift invariant. For and , it follows that

Next we will show that by contradiction. If there exists some such that, then

So. Therefore, which implies that since. Consequently,. This leads to a contradiction since. Assume that M is a shift invariant subspace contained in X. Obviously. Thus,. So. The result follows. The proof is completed.

Lemma 3. Let X and Y be affine subspaces of with. Let M and N be generating shift invariant subspaces for X and Y respectively. Then is an affine subspace of with as a generating shift invariant subspace.

Proof. Since and, it follows that

The proof is completed.

Lemma 4. Assume is a monotone sequence of subspaces in a Hilbert space and give a subspace satisfying for each. Then

Proof. Since is a monotone sequence of subspaces and, , we have is also a monotone sequence. Then the first equality follows by Lemma 2. For, there exists some such that, namely and. Then. Thus. So. For the other direction, without loss of generality, assume that is increasing. By Lemma 2,

which shows that. The proof is completed.

Lemma 5. Let X be an affine subspace of and Q be the maximal shift invariant subspace contained in X. Define. Then the following hold:

1) and for;

2), if and only if X is a reducing subspace of;

3), is in any reducing subspace of containing X.

Proof. 1): Note that we only need to show and. While follows by Proposition 2. So. Thus we have

2): Since Q is shift invariant and, it follows that

If X is a reducing subspace, then. By the definition of V, we have. If, then, which shows that X is shift invariant. Thus X is a reducing subspace.

3): By 1) and 2), we have for all j, with. Thus for each,

. Therefore. Let M be a reducing subspace containing X. Then. So for each,. Hence. The proof is completed.

Proposition 4. Let X and Y be affine subspaces of satisfying. Let Q and S be the maximal shift invariant subspaces contained in X and Y respectively. Define. Then is the maximal shift invariant subspace contained in.

Proof. Let M be a shift invariant subspace contained in. By Lemma 3 and the maximality of S as a shift invariant subspace in Y, we have. Note that and. Then

. So. Hence. Therefore. The proof is completed.

Proposition 5. Let X and Y be affine subspaces of satisfying. Let Q and S be the maximal

shift invariant subspaces contained in X and Y respectively. Define. Then is an affine subspace of if and only if.

Proof. According to Proposition 4, is the maximal shift invariant subspace in. If is an affine subspace, then by Lemma 3, is a generating shift invariant subspace for, i.e.,

. Now suppose. Since and by Lemma 5 for, we have for. Thus by Lemma 4,

Write and. Then. In fact,

Hence

due to the fact that is equivalent to for a given Hilbert space with its two subspaces and. Also by Lemma 4, we have

So. The proof is completed.

Proposition 6. Let X and Y be two affine subspaces of with. Then the following holds.

1) is affine if X is reducing;

2) if Y is reducing and is affine, where and Q is the maximal shift invariant subspace in X.

Proof. 1): By Lemma 5, with X being a reducing subspace. Then is the maximal shift invariant subspace for by Proposition 4. Now we only need to show that

. Note that

due to the facts that and. So by Lemma 1,

Observe that since is invariant under for. Therefore,

2): According to Proposition 5, it follows that. By Lemma 4,

which shows that, i.e.,. Since is contained in any reducing space containing X by Lemma 4,. Consequently. The proof is completed.

Theorem 7. Let X be an affine subspace of. Then the following holds.

1) There exist a shift invariant subspace M in X such that for with, and;

2) If X is a non-zero reducing subspace and, then there exist two purely non-reducing affine subspaces X₁ and X₂ such that;

3) If X is non-zero and not reducing, then there exists a unique decomposition with X₁ be reducing and X₂ being purely non-reducing;

4) If X is non-zero and, then X is the orthogonal direct sum of at most three purely non-reducing affine subspace.

Proof. 1): By Proposition 1, it follows that, where M₁ is some shift invariant subspace in X and Y is a reducing subspace. If, then the result follows. Otherwise, there is a such that is an orthonormal basis for Y. Let and define . Note that by the definition of M₁ in the proof of Proposition 1, it follows that for with. So with when and.

2): Let be an orthonormal wavelet for X. Choose k, such that and. Let be a set of representatives of distinct cosets in. Then

is a set of representatives of distinct cosets in.

Indeed, for, clearly if. Now we consider the case. Observe that equals to. Note that. So. Define two subsets and of X and two shift invariant subspaces P and M as follows:

Then forms an orthonormal basis for P due to the fact that is an orthonormal wavelet for X. The same to M. Define

Then. Next, we will show X₁ is a purely non-reducing affine subspace. Write

Obviously Q is a shift invariant subspace contained in X₁ and. According to Proposition 2, it suffices to show that Q is the maximal shift invariant subspace contained in X₁. Also by Proposition 3, it is

enough to show, where. Observe that for each,

Then for each,

since for all. Therefore, for each,

Hence

Thus. So X₁ is a purely non-reducing affine subspace. Similarly to X₂.

3): Let X be a non-reducing affine subspace of and X₁ be the maximal reducing subspace contained in X. Write. Then X₂ is affine by Proposition 6 and X₂ is purely non-reducing since X₁ is the maximal reducing subspace in X. Also note that the orthogonal complement of a reducing space within another reducing space is always reducing. Then the uniqueness follows.

4): 4) follows after 2) and 3). The proof is completed.

Acknowledgements

We thank the Editor and the referee for their comments. This work is funded by the National Natural Science Foundation of China (Grant No. 11326089), the Education Department Youth Science Foundation of Jiangxi Province (Grant No. GJJ14492) and PhD Research Startup Foundation of East China Institute of Technology (Grant No. DHBK2012205).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Weiss, G. and Wilson, E.N. (2001) The Mathematical Theory of Wavelets. In: Byrnes, J.S., Ed., Twentieth Century Harmonic Analysis-A Celebration//Proceedings of the NATO Advanced Study Institute, Kluwer Academic Publishers, Dordrecht, 329-366.
[2]	Dai, X., Diao, Y., Gu, Q. and Han, D. (2002) Frame Wavelets in Subspaces of . Proceedings of the American Mathematical Society, 130, 3259-3267. http://dx.doi.org/10.1090/S0002-9939-02-06498-5
[3]	Zhou, F.Y. and Li, Y.Z. (2010) Multivariate FMRAs and FMRA Frame Wavelets for Reducing Subspaces of . Kyoto Journal of Mathematics, 50, 83-99. http://dx.doi.org/10.1215/0023608X-2009-006
[4]	Dai, X., Diao, Y. and Gu, Q. (2002) Subspaces with Normalized Tight Frame Wavelets in . Proceedings of the American Mathematical Society, 130, 1661-1667. http://dx.doi.org/10.1090/S0002-9939-01-06257-8
[5]	Dai, X., Diao, Y., Gu, Q. and Han, D. (2003) The Existence of Subspace Wavelet Sets. Journal of Computational and Applied Mathematics, 155, 83-90. http://dx.doi.org/10.1016/S0377-0427(02)00893-2
[6]	Lian, Q.F. and Li, Y.Z. (2007) Reducing Subspace Frame Multiresolution Analysis and Frame Wavelets. Communications on Pure and Applied Analysis, 6, 741-756. http://dx.doi.org/10.3934/cpaa.2007.6.741
[7]	Li, Y.Z. and Zhou, F.Y. (2010) Affine and Quasi-Affine Dual Frames in Reducing Subspaces of . Acta Mathematica Sinica (Chinese Edition), 53, 551-562.
[8]	Gu, Q. and Han, D. (2009) Wavelet Frames for (Not Necessarily Reducing) Affine Subspaces. Applied and Computational Harmonic Analysis, 27, 47-54. http://dx.doi.org/10.1016/j.acha.2008.10.006
[9]	Gu, Q. and Han, D. (2011) Wavelet Frames for (Not Necessarily Reducing) Affine Subspaces II: The Structure of Affine Subspaces. Journal of Functional Analysis, 260, 1615-1636. http://dx.doi.org/10.1016/j.jfa.2010.12.020
[10]	Zhou, F.Y. and Li, Y.Z. (2013) A Note on Wavelet Frames for Affine Subspaces of . Acta Mathematica Sinica (Chinese Edition), 33A, 89-97.