A Real Version of the Dirac Equation and Its Coupling to the Electromagnetic Field ()
1. Introduction
In modern elementary particle physics the complex Dirac equation [1] plays a fundamental role and is used in the standard model (SM) to describe the charged fermions (see, e.g., the textbooks by Lee [2] and Kaku [3] ), which are represented in terms of four-component complex spinor fields or two-component complex Weyl spinor fields [4] in the chiral representation for the massless case. The aim of the present work is to show that charged fermions can also be described by a purely real Dirac equation that does not involve any complex numbers at all but only real matrices and spinors. This approach is quite different from the abstract mathematical way of Hestenes [5] , who reformulated the Dirac theory completely in terms of a real Clifford algebra characterizing the geometrical properties of space-time. Our approach also differs substantially from the treatment by Ljolje [6] , who argued that the analogy with the classical electromagnetic field suggests a full description also of the Dirac field in the real domain. In this paper, the gauge symmetry considered thereafter for the coupling of fermions to an electromagnetic field is based on the SO(2) group. It is, while being its adjoint representation, closely related to the U(1) group which is commonly used in electrodynamic gauge theory of the standard com- plex Dirac equation.
It is well known that fermions described by the real four-component Majorana [7] - [9] equation can not be coupled to the electromagnetic field. Therefore that equation can only describe neutral fermions and has found no application in the SM. We will show, however, that for the real version of the Dirac equation the coupling of charged fermions to an electromagnetic field is possible, and can be retained if in that equation the real and imaginary part of a complex Dirac spinor field are assembled in a doublet associated with the SO(2) symmetry group. This arrangement enables a matrix coupling to the electromagnetic field. We will subsequently derive the eigenfunctions of this real version of the Dirac in some detail, and also discuss some problems arising with the evaluation of the related Lorentz-invariant bilinear form that appear in the mass term.
The outline of the paper is as follows: First, the four-component real Majorana equation is briefly discussed as the classical paradigm for a real spinor field equation. Second, the covariant derivative in electromagnetic gauge theory is reconsidered, and a way opened to introduce electromagnetism into a real spinor field equation. Third, the complex Dirac equation including an electromagnetic field will be transformed into a real Dirac equation for an eight-component real spinor field. Through this procedure it becomes obvious how the electromagnetic field couples to charged fermions (e.g., electrons and positrons) when being described by real spinor fields. The symmetries of the resulting real Dirac equation are also discussed. Fourth, the eigenfunctions of the real Dirac equation are derived. Fifth, the properties of bilinear forms are shortly addressed, and then we consider similarity transformations. Finally, the conclusions are presented.
2. The Majorana Equation
At the start we rederive the real four-component spinor Majorana equation, without recourse to the Dirac equation (thereby following the recent work of Aste and Marsch [10] - [12] ). The Majorana equation with a mass term provides a useful description of massive neutrinos. Its solutions include both kinetic helicities, as it is required for a massive relativistic particle.
In the subsequent algebra we make use of conventional symbols, notations and definitions, and use units of . The covariant four-momentum operator, defined as
. The covariant four-momentum operator, defined as , acts for example on the scalar field
, acts for example on the scalar field  or the real four-component spinor field
or the real four-component spinor field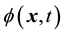 . Insertion of the differential operator
. Insertion of the differential operator  into the relativistic energy and momentum relation, written in manifestly covariant form as mass-shell con- dition
into the relativistic energy and momentum relation, written in manifestly covariant form as mass-shell con- dition , readily yields the real Klein-Gordon equation [13] [14]
, readily yields the real Klein-Gordon equation [13] [14]
 (1)
(1)
for the scalar field . This equation is the starting point of any quantum field theory and involves only the second-order differential d’Alembert operator which obviously is invariant under a Lorentz transformation. Equation (1) can formally be linearized to read
. This equation is the starting point of any quantum field theory and involves only the second-order differential d’Alembert operator which obviously is invariant under a Lorentz transformation. Equation (1) can formally be linearized to read
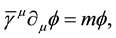 (2)
(2)
with appropriately defined real spinor field , and by introduction of the non-commuting matrix operators
, and by introduction of the non-commuting matrix operators . Here we indicated the real gamma matrices as appearing in (2) by a top bar, in order to avoid confusion with the standard nomenclature of the Dirac [1] equation. By squaring now equation (2) one finds that, for reproducing (1), the gammas have to obey the algebra
. Here we indicated the real gamma matrices as appearing in (2) by a top bar, in order to avoid confusion with the standard nomenclature of the Dirac [1] equation. By squaring now equation (2) one finds that, for reproducing (1), the gammas have to obey the algebra
 (3)
(3)
Here 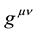 is the Minkowskian metric tensor, and the brackets denote the anticommutator. We shall derive in the course of this paper various forms of the gamma matrix operators.
is the Minkowskian metric tensor, and the brackets denote the anticommutator. We shall derive in the course of this paper various forms of the gamma matrix operators.
Apparently, the condition (3) can be fulfilled by the real 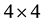 gamma matrices derived from the repre- sentation first found by Majorana [7] , which then makes (2) a real spinor field equation. It is easily transformed into the standard Dirac equation by use of the purely imaginary gamma matrices
gamma matrices derived from the repre- sentation first found by Majorana [7] , which then makes (2) a real spinor field equation. It is easily transformed into the standard Dirac equation by use of the purely imaginary gamma matrices , in which case the spinor field
, in which case the spinor field  would also have to be complex and then is conventionally denoted by
would also have to be complex and then is conventionally denoted by![]() . In order to formulate the Dirac matrices in their Majorana representation, we make use of the Pauli [13] matrices and the related three-vector
. In order to formulate the Dirac matrices in their Majorana representation, we make use of the Pauli [13] matrices and the related three-vector![]() . The three Pauli matrices are defined as:
. The three Pauli matrices are defined as:
![]() (4)
(4)
Obviously, all three sigma matrices mutually anti-commute with each other and, when being squared, are equal to the ![]() unit matrix. The three lambda matrices are all real and also mutually anti-commute, and one finds
unit matrix. The three lambda matrices are all real and also mutually anti-commute, and one finds![]() , but note that
, but note that![]() . They will be used later to build up real higher-dimensional gamma matrices. Depending upon its dimension, the unit matrix will be denoted as
. They will be used later to build up real higher-dimensional gamma matrices. Depending upon its dimension, the unit matrix will be denoted as ![]() for two, four or eight dimensions. To ease the notation we may omit the index and simply write 1 for the unit matrix if no confusion can arise. The corresponding null matrices are always simply denoted by 0.
for two, four or eight dimensions. To ease the notation we may omit the index and simply write 1 for the unit matrix if no confusion can arise. The corresponding null matrices are always simply denoted by 0.
In terms of the above lambda matrices the Majorana gamma matrices (see, e.g. Kaku [3] ) can be written as:
![]() (5)
(5)
whereby ![]() and
and![]() , and
, and ![]() runs from 1 to 3. Thus in the Majorana representation,
runs from 1 to 3. Thus in the Majorana representation,
![]() is antisymmetric, whereas
is antisymmetric, whereas ![]() is symmetric, where the superscript T indicates the
is symmetric, where the superscript T indicates the
transposed matrix. The standard representation of the Dirac matrices [3] is obtained from (5) by means of a similarity transformation. For subsequent use we also introduce another name for the real gamma matrix, writing it as![]() , with the three-vector matrix
, with the three-vector matrix![]() , the definition of which can be read of from (5). The Majorana equation then reads
, the definition of which can be read of from (5). The Majorana equation then reads
![]() (6)
(6)
We emphasize that the Majorana equation, while being real, has two degrees of freedom (![]() is a real four- component spinor field) less than the standard Dirac equation (in which
is a real four- component spinor field) less than the standard Dirac equation (in which ![]() is a complex four-component spinor field), and thus can apply only to neutral fermions. However, as shown below we can obtain a real ver- sion of the Dirac equation, which looks similar than (6) but involves real eight-component spinor fields. Before doing so, we discuss the related covariant derivative.
is a complex four-component spinor field), and thus can apply only to neutral fermions. However, as shown below we can obtain a real ver- sion of the Dirac equation, which looks similar than (6) but involves real eight-component spinor fields. Before doing so, we discuss the related covariant derivative.
3. Covariant Derivative in Electromagnetic Gauge Theory
As is well known from the classical work of Klein, Pauli and Weisskopf [3] [14] [15] , the real scalar Klein- Gordon field can also be used for charged particles, namely by considering two independent scalar fields which both obey the Klein-Gordon equation and are associated with the positively and negatively charged bosons having the same mass. They can be arranged in a complex composite scalar field, such that![]() . The same approach may be adopted for the real Majorana equation (2) or (6), a procedure that is in the spirit of the original paper by Majorana [7] , and which yields
. The same approach may be adopted for the real Majorana equation (2) or (6), a procedure that is in the spirit of the original paper by Majorana [7] , and which yields ![]() for the combined Majorana spinor field of electron and positron, both obeying separately the real Majorana equation with the same mass. By insertion of the above complex spinor field
for the combined Majorana spinor field of electron and positron, both obeying separately the real Majorana equation with the same mass. By insertion of the above complex spinor field ![]() into (2) and by use of the Dirac matrix
into (2) and by use of the Dirac matrix ![]() in Majorana represen- tation, we then retain of course the complex standard Dirac equation which reads
in Majorana represen- tation, we then retain of course the complex standard Dirac equation which reads
![]() (7)
(7)
This equation obeys U(1) symmetry, meaning that the spinor field ![]() can be multiplied by an arbitrary phase factor
can be multiplied by an arbitrary phase factor ![]() without changing the physical content of the theory. The symmetry is global for constant
without changing the physical content of the theory. The symmetry is global for constant![]() , or local if it depends on the coordinate
, or local if it depends on the coordinate ![]() (which we use for
(which we use for ![]() as a shorthand). Correspondingly, the electromagnetic interaction (with the related gauge field
as a shorthand). Correspondingly, the electromagnetic interaction (with the related gauge field ![]() and coupling constant
and coupling constant![]() ) must be introduced by the minimal coupling principle [3] , whereby the space-time derivative
) must be introduced by the minimal coupling principle [3] , whereby the space-time derivative ![]() is replaced in (7) by the covariant derivative
is replaced in (7) by the covariant derivative
![]() (8)
(8)
However, apparently this procedure does not work for the real Majorana Equation (2) or (6), without destroy- ing their real nature. So, the real four-component Majorana equation can not be coupled to an electromagnetic field (and also not to other gauge fields when being associated with complex phase factors) by means of the minimal coupling in the above form.
Yet, there is another way to introduce electromagnetism in a real field equation, if we just assemble the real and imaginary parts of a complex spinor ![]() in an expanded two-component spinor, which corresponds to the symmetry group SO(2) (that is the adjoint representation of the U(1) symmetry group) of rotations in a plane. So let us consider a complex four-component spinor
in an expanded two-component spinor, which corresponds to the symmetry group SO(2) (that is the adjoint representation of the U(1) symmetry group) of rotations in a plane. So let us consider a complex four-component spinor ![]() and arrange it in a eight-component real spinor, such that
and arrange it in a eight-component real spinor, such that![]() . The phase transformation
. The phase transformation ![]() can then be written equivalently in matrix (of determinant unity) form as
can then be written equivalently in matrix (of determinant unity) form as ![]() with the antisymmetric matrix
with the antisymmetric matrix
![]() (9)
(9)
which is a generator of the SO(2) group. Here use has been made of![]() , and apparently,
, and apparently, ![]() obeys
obeys![]() . In this way the covariant derivative can become real and be formally written
. In this way the covariant derivative can become real and be formally written
![]() (10)
(10)
As shown below, when the Dirac equation is brought into its real form the SO(2) symmetry is obeyed instead of U(1), and thus a Dirac fermion can be charged if it is described in terms of a real eight-component spinor field.
The transformation of the spinor field for a spatio-temporal varying phase ![]() corresponds now to
corresponds now to![]() . The covariant derivative of the field [3] [16] then transforms like the field itself, and thus gauge invariance is ensured. Namely we have
. The covariant derivative of the field [3] [16] then transforms like the field itself, and thus gauge invariance is ensured. Namely we have
![]() (11)
(11)
if the gauge field is transformed as![]() , which is the usual gauge transformation of electrodynamics.
, which is the usual gauge transformation of electrodynamics.
4. The Real Dirac Equation
Following the reasoning in the previous sections, we now want to derive a real version of the Dirac equation. The complex standard Dirac equation for ![]() including the electromagnetic field reads
including the electromagnetic field reads
![]() (12)
(12)
The Dirac matrices in their standard form can be written concisely as
![]() (13)
(13)
Using the above lambda matrices, we obtain
![]() (14)
(14)
Note that the three components of the vector ![]() anticommute mutually because of the properties of the lambda matrices, and they all anticommute also with
anticommute mutually because of the properties of the lambda matrices, and they all anticommute also with![]() . Therefore the Dirac gamma matrices obey the Cli- fford algebra
. Therefore the Dirac gamma matrices obey the Cli- fford algebra
![]() (15)
(15)
We can now decompose the complex Dirac Equation (12) into its real and imaginary parts. Thereby we assemble again the real and imaginary parts of a complex four-component Dirac spinor, ![]() , in an expanded eight-component real spinor,
, in an expanded eight-component real spinor, ![]() , like we did above when discussing the covariant derivate. After considerable algebra one can collect the various terms in four blown-up
, like we did above when discussing the covariant derivate. After considerable algebra one can collect the various terms in four blown-up ![]() real gamma matrices, which we name
real gamma matrices, which we name![]() , with the subscript indicating that they are all real. This real Dirac equation can be written concisely as
, with the subscript indicating that they are all real. This real Dirac equation can be written concisely as
![]() (16)
(16)
The gamma matrices have a ![]() block form, can be built on the above Dirac matrices and be written as
block form, can be built on the above Dirac matrices and be written as![]() , with the three-vector matrix
, with the three-vector matrix![]() . Thus we obtain the four real gamma matrices in the form
. Thus we obtain the four real gamma matrices in the form
![]() (17)
(17)
These four matrices commute with![]() , and like in (3) obey the algebraic relation
, and like in (3) obey the algebraic relation
![]() (18)
(18)
Let us discuss the general symmetries of the real Dirac equation. Concerning its space-time symmetries, we define conventionally the time and space coordinate inversion operations as ![]() and
and![]() , acting on the spinor field
, acting on the spinor field ![]() as follows,
as follows, ![]() , and
, and![]() . We further note that the coordinate reversal operators
. We further note that the coordinate reversal operators ![]() and
and ![]() commute with
commute with ![]() and
and![]() . It then is easy to show that the real Dirac equation (16) is invariant under time reversal, if given by
. It then is easy to show that the real Dirac equation (16) is invariant under time reversal, if given by![]() , and parity, if given by
, and parity, if given by![]() . The operator
. The operator ![]() is defined by the product of the three (mutually anticommuting) spatial gamma matrices, and as such commutes with each of them individually. However, it anticommutes with temporal gamma matrix
is defined by the product of the three (mutually anticommuting) spatial gamma matrices, and as such commutes with each of them individually. However, it anticommutes with temporal gamma matrix![]() , as required for the time-reversal operation. We finally have
, as required for the time-reversal operation. We finally have
![]() (19)
(19)
whereby we find for the product of Dirac matrices the result
![]() (20)
(20)
The charge conjugation operation ![]() requires an operator that commutes with all
requires an operator that commutes with all ![]() but anticommutes with
but anticommutes with![]() , in order to be able to change the sign of the charge
, in order to be able to change the sign of the charge ![]() in (16). Close inspection of the gamma matrices makes clear that it can be defined by the help of the matrix
in (16). Close inspection of the gamma matrices makes clear that it can be defined by the help of the matrix
![]() (21)
(21)
which is found to obey![]() , and apparently to anticommute with
, and apparently to anticommute with![]() . Therefore, we can define charge con- jugation by
. Therefore, we can define charge con- jugation by![]() . Consequently, if
. Consequently, if ![]() solves (16), then
solves (16), then ![]() solves the charge-conjugated equation, and thus the real Dirac equation describes both a charged fermion and its antiparticle of opposite charge, yet without making use of complex numbers anywhere. Obviously, the matrix
solves the charge-conjugated equation, and thus the real Dirac equation describes both a charged fermion and its antiparticle of opposite charge, yet without making use of complex numbers anywhere. Obviously, the matrix ![]() plays kind of the role of the imaginary unit
plays kind of the role of the imaginary unit![]() . Furthermore, if
. Furthermore, if ![]() solves (16) then
solves (16) then ![]() solves it as well, and similarly, if
solves it as well, and similarly, if ![]() solves (16)
solves (16) ![]() solves it also. Thus the real Dirac equation governing the charged spinor field
solves it also. Thus the real Dirac equation governing the charged spinor field ![]() is invariant under the combined action of the triple transformation
is invariant under the combined action of the triple transformation![]() . Trivially, for
. Trivially, for ![]() or
or![]() , the real Dirac equation still remains invariant under
, the real Dirac equation still remains invariant under![]() , which essentially amounts to interchanging the upper and lower components
, which essentially amounts to interchanging the upper and lower components![]() , respectively
, respectively![]() , of the spinor field
, of the spinor field![]() , but multiplied with
, but multiplied with![]() .
.
Finally, let us briefly discuss chiral symmetry. The real chiral matrix is defined appropriately as ![]() , from which we obtain
, from which we obtain
![]() (22)
(22)
which yields![]() . By definition, it anticommutes with all four gamma matrices, and thus chiral sym- metry implies, that if
. By definition, it anticommutes with all four gamma matrices, and thus chiral sym- metry implies, that if ![]() solves the real Dirac Equation (16), then
solves the real Dirac Equation (16), then ![]() solves it with a negative mass term. Furthermore,
solves it with a negative mass term. Furthermore, ![]() , but
, but![]() . We can define as usually the idempotent pro-
. We can define as usually the idempotent pro-
jection operators by![]() , by means of which any spinor field can be decomposed into its right- and
, by means of which any spinor field can be decomposed into its right- and
left-chiral components, i.e.![]() , which yields two Dirac equations, one for each of them. These equ- ations read
, which yields two Dirac equations, one for each of them. These equ- ations read
![]() (23)
(23)
and are coupled by the mass term which obviously breaks chiral symmetry.
5. Eigenfunctions of the Real Dirac Equation
We return to the real Dirac Equation (16) with the aim to derive its eigenfunctions for![]() . For that purpose, we write it here in terms of the beta and three-vector gamma operators
. For that purpose, we write it here in terms of the beta and three-vector gamma operators ![]() and
and![]() , of which we basically only need their algebraic properties, but which are
, of which we basically only need their algebraic properties, but which are ![]() matrices in matrix representation. To ease the notation we omit from now on their index R, and thus obtain the real Dirac equation as
matrices in matrix representation. To ease the notation we omit from now on their index R, and thus obtain the real Dirac equation as
![]() (24)
(24)
It resembles very much the Majorana Equation (6), with the difference being in the dimension of the gamma matrix representation and the associated spinors. Since Equation (24) is real, and as each component of ![]() must obey the Klein-Gordon equation, we make the general sine-cosine propagating wave ansatz:
must obey the Klein-Gordon equation, we make the general sine-cosine propagating wave ansatz:
![]() (25)
(25)
with free real amplitude ![]() and phase angle
and phase angle![]() . Here
. Here![]() . The two polarization spinors, U and V, must of course also be real. Upon inserting the ansatz into (24) we obtain the linked polari- zation spinor equations:
. The two polarization spinors, U and V, must of course also be real. Upon inserting the ansatz into (24) we obtain the linked polari- zation spinor equations:
![]() (26)
(26)
![]() (27)
(27)
By insertion of the first into the second equation, or vice versa, the relativistic dispersion relation is obtained from:
![]() (28)
(28)
which yields the two eigenvalues:
![]() (29)
(29)
The negative root in Equation (29) is related to antiparticles, the positive one to particles. By solving (26) for ![]() and inserting it back into (25), or vice versa, we obtain the two alternative solutions (with amplitude and phase which we chose to be unity and zero for the present calculation) which read
and inserting it back into (25), or vice versa, we obtain the two alternative solutions (with amplitude and phase which we chose to be unity and zero for the present calculation) which read
![]() (30)
(30)
![]() (31)
(31)
The second solution is obtained from first one if the free phase is chosen as ![]() and
and ![]() replaced by
replaced by![]() , and thus there is no new information. In what follows we therefore just consider
, and thus there is no new information. In what follows we therefore just consider ![]() and omit the subscript again. When summing in a Fourier decomposition over the momentum
and omit the subscript again. When summing in a Fourier decomposition over the momentum![]() , one may equally well sum over
, one may equally well sum over![]() , since it is a mute index. For the two possible eigenvalues in (29) we therefore define the particle solution as
, since it is a mute index. For the two possible eigenvalues in (29) we therefore define the particle solution as ![]() and the antiparticle solution as
and the antiparticle solution as![]() . Then the bracket in front of
. Then the bracket in front of ![]() in (30) remains similar for both solutions and we obtain
in (30) remains similar for both solutions and we obtain
![]() (32)
(32)
![]() (33)
(33)
where the polarization vector is defined by![]() , and amplitudes with
, and amplitudes with ![]() and phases with
and phases with ![]() have explicitly been added. Note that charge conjugation mediated by the matrix
have explicitly been added. Note that charge conjugation mediated by the matrix ![]() of Equation (21) does not affect the kinetic part of these spinor fields, as it commutes with
of Equation (21) does not affect the kinetic part of these spinor fields, as it commutes with ![]() and
and ![]() and therefore only acts on the polarization spinor
and therefore only acts on the polarization spinor![]() .
.
Returning now to the standard Dirac Equation (7), we can chose for it the standard basis
![]() (34)
(34)
corresponding to particles ![]() and antiparticles
and antiparticles![]() , as we have
, as we have ![]() and
and![]() , and thus we retain the usual covariant normalization
, and thus we retain the usual covariant normalization ![]() and
and![]() . Inserting these basis vectors into the solution for the complex Dirac equation provides us with an orthogonal set of four eigenstates, which are the standard textbook [3] solutions. Admittedly, for the complex Dirac equation it seems more meaningful to use exponentials instead of trigonometric functions. For the real Dirac (and the Majorana) equation they are a natural choice in the ansatz (25).
. Inserting these basis vectors into the solution for the complex Dirac equation provides us with an orthogonal set of four eigenstates, which are the standard textbook [3] solutions. Admittedly, for the complex Dirac equation it seems more meaningful to use exponentials instead of trigonometric functions. For the real Dirac (and the Majorana) equation they are a natural choice in the ansatz (25).
How many physical degrees of freedom does the real Dirac equation have? Of course it should not be more than the complex one, which has four, as the complex spinor fields ![]() and the adjoint one
and the adjoint one ![]() are canoni- cally conjugate variables in the Lagrange formalism [3] , or more precisely it is
are canoni- cally conjugate variables in the Lagrange formalism [3] , or more precisely it is ![]() which is the conjugate “momentum” of the spinor field
which is the conjugate “momentum” of the spinor field![]() . Thus there are in fact only 4 degrees of freedom, equal to the dimension of the underlying vector space defining the complex Dirac spinors, and thus we obtain, as described by the fun- damental basis (34) above, the particle and its antiparticle, each having two spin degrees of freedom. The same must apply to the real Dirac equation. However, while decomposing the field
. Thus there are in fact only 4 degrees of freedom, equal to the dimension of the underlying vector space defining the complex Dirac spinors, and thus we obtain, as described by the fun- damental basis (34) above, the particle and its antiparticle, each having two spin degrees of freedom. The same must apply to the real Dirac equation. However, while decomposing the field ![]() into its real and imaginary parts, both have been treated as independent variables, and thus the resulting real vector space is 8-dimensional like the phase space of the complex Dirac equation, although there are only four independent physical degrees of freedom.
into its real and imaginary parts, both have been treated as independent variables, and thus the resulting real vector space is 8-dimensional like the phase space of the complex Dirac equation, although there are only four independent physical degrees of freedom.
Let us now determine the basis spinors of the real Dirac equation. Obviously, in the above general solutions (32) and (33) the polarization spinors can be chosen freely, and the question then arises how to chose them adequately for the real Dirac equation. For that purpose we make use of the standard basis vectors (34), and with their help construct the new extended fundamental basis as follows
![]() (35)
(35)
corresponding to particle and antiparticle states arranged in doublets of four-component spinors. Note that these basis spinors are eight-dimensional, corresponding to the dimension of the phase space of the complex standard Dirac equation, and form an orthonormal basis of the vector space of the real Dirac equation. Its solution is the doublet spinor field![]() , which contains the spinor field
, which contains the spinor field ![]() of the complex Dirac equation, namely its real part
of the complex Dirac equation, namely its real part ![]() in the upper and its imaginary part
in the upper and its imaginary part ![]() in the lower component of
in the lower component of![]() . Upon inserting the eight basis spinors (35) into the solutions (32) and (33), we obtain, respectively, four spinors
. Upon inserting the eight basis spinors (35) into the solutions (32) and (33), we obtain, respectively, four spinors ![]() and
and ![]() (where
(where ![]() runs from 1 to 4), which are eight linearly independent states of the real Dirac equation, correspond- ing respectively to a particle and its antiparticle, whereby each of them has momentum
runs from 1 to 4), which are eight linearly independent states of the real Dirac equation, correspond- ing respectively to a particle and its antiparticle, whereby each of them has momentum ![]() and energy
and energy ![]() and two spin degrees of freedom, or two states of opposite kinetic helicity.
and two spin degrees of freedom, or two states of opposite kinetic helicity.
Let us also discuss briefly how the charge conjugation and the chiral operator act on the basis spinors. We recall the definition of the charge conjugation, which is given by![]() . It obeys
. It obeys ![]() and, when using its matrix representation (21), is found to link the particle and antiparticle states like follows,
and, when using its matrix representation (21), is found to link the particle and antiparticle states like follows,
![]() (36)
(36)
showing the tight connection between particle and antiparticle spinors. As the charge conjugation operator ![]() anticommutes with
anticommutes with![]() , the particle and its antiparticle, as was to be expected, have opposites charges. Chiral symmetry is closely connected with charge exchange, because applying the operator
, the particle and its antiparticle, as was to be expected, have opposites charges. Chiral symmetry is closely connected with charge exchange, because applying the operator ![]() on the particle spinors in (35) returns antiparticle spinors and vice versa. So we obtain
on the particle spinors in (35) returns antiparticle spinors and vice versa. So we obtain
![]() (37)
(37)
which is in consistent with the fact that ![]() turns a solution of the real Dirac equation for positive mass into one with a negative mass, i.e. a particle into its antiparticle.
turns a solution of the real Dirac equation for positive mass into one with a negative mass, i.e. a particle into its antiparticle.
6. Bilinear Forms Associated with the Real Dirac Equation
Like for the complex Dirac equation, bilinear forms involving the spinor field and its adjoint play an important role in a relativistic field theory. Therefore, we must consider such Lorentz-invariant bilinear forms (see, e.g., [3] ) like![]() , which also determines the mass term in the Lagrangian density in the complex Dirac equation. For the two Equations (6) and (24) we obtain similar bilinear forms, namely
, which also determines the mass term in the Lagrangian density in the complex Dirac equation. For the two Equations (6) and (24) we obtain similar bilinear forms, namely
![]() (38)
(38)
![]() (39)
(39)
where ![]() and
and ![]() have been used, which both differ from the Dirac matrix
have been used, which both differ from the Dirac matrix![]() , which
, which
means ![]() is hermitian and symmetric, whereas the above two operators or matrices are antihermitian, that is antisymmetric. As such they can not have real eigenvalues or eigenvectors, which causes a serious problem that
is hermitian and symmetric, whereas the above two operators or matrices are antihermitian, that is antisymmetric. As such they can not have real eigenvalues or eigenvectors, which causes a serious problem that
is intimately connected with the negative sign in front of the metric (3), which requires![]() . In fact, we
. In fact, we
have![]() , and
, and![]() . But remember that in contrast
. But remember that in contrast![]() ,
, ![]() and
and![]() , and thus that for any three-vector
, and thus that for any three-vector ![]() one has
one has![]() ,
, ![]() and
and![]() .
.
Using these mathematical properties one finds after some algebra by means of (32) and (33) that for any pair of solution field spinors we have![]() , with the index I and J being A or P, and i and j run from 1 to 4. That means orthogonality or normalization of the spinor fields just depends on the Lorentz invariant bilinear form (i.e., the inner product) of the respective polarization spinors involved.
, with the index I and J being A or P, and i and j run from 1 to 4. That means orthogonality or normalization of the spinor fields just depends on the Lorentz invariant bilinear form (i.e., the inner product) of the respective polarization spinors involved.
Let us consider a general polarization spinor of the real Dirac equation![]() , where
, where ![]() and
and ![]() stand for any real 4-component spinor constructed on the basis (34). Then the related covariant bilinear form reads
stand for any real 4-component spinor constructed on the basis (34). Then the related covariant bilinear form reads
![]() (40)
(40)
which vanishes identically, in particular for any pair of the basis spinors in Equation (34), since beta is sym- metric:![]() . Similarly, for the real Majorana bilinear form with real spinor
. Similarly, for the real Majorana bilinear form with real spinor ![]() and with
and with![]() , where
, where ![]() and
and ![]() are real two-component spinors, we obtain the result
are real two-component spinors, we obtain the result
![]() (41)
(41)
since![]() . The implications of the vanishing bilinear forms were for the Majorana equation already discussed long ago by Case [8] [9] , and recently again by Pal [17] who emphasized that the solution to this dilemma is to consider anticommuting fermion quantum fields instead of classical ones, what we have done here so far. Since bilinear forms such as in Equations (38)-(39) play a key role in relativistic quantum field theory, we must conclude that Lorentz invariance forces one to consider quantized versions of the real “classical” fermion fields discussed before.
. The implications of the vanishing bilinear forms were for the Majorana equation already discussed long ago by Case [8] [9] , and recently again by Pal [17] who emphasized that the solution to this dilemma is to consider anticommuting fermion quantum fields instead of classical ones, what we have done here so far. Since bilinear forms such as in Equations (38)-(39) play a key role in relativistic quantum field theory, we must conclude that Lorentz invariance forces one to consider quantized versions of the real “classical” fermion fields discussed before.
The transition to quantization is readily achieved, if we rewrite (omitting the index P here) the real spinor field (32) by replacing the trigonometric by exponential functions. We then obtain
![]() (42)
(42)
with a new abbreviation that is the operator![]() . It is real and has the following
. It is real and has the following
properties![]() ,
, ![]() , and anticommutes with beta as follows:
, and anticommutes with beta as follows:![]() . The complex amplitude
. The complex amplitude
is![]() , which may be normalized to a module of unity. Using the properties of the capital gammas, it is straightforward to show that still
, which may be normalized to a module of unity. Using the properties of the capital gammas, it is straightforward to show that still![]() . Note that of course
. Note that of course ![]() for the real Dirac equation.
for the real Dirac equation.
To render (42) becoming a quantum field, we just have to promote the amplitudes to fermion annihilation and creation operators that obey the canonical anti-commutation rule
![]() (43)
(43)
With these comments and conclusions we shall close the discussion of the bilinear forms which determine the mass term in the Lagrangian density.
7. Similarity Transformations
Finally, we will return to the Majorana equation and present its eight-component version which can be obtained by a similarity transformation from the real Dirac Equation (16). The similarity transformation matrix associated with the standard Dirac equation can be written as
![]() (44)
(44)
By definition it is unitary and has the property![]() . The real Majorana matrices, which were quoted already in Equation (5), are obtained from the Dirac matrices in standard representation through the trans- formation
. The real Majorana matrices, which were quoted already in Equation (5), are obtained from the Dirac matrices in standard representation through the trans- formation
![]() (45)
(45)
In a similar way we can now subject the real Dirac Equation (16) to a corresponding similarity transformation defined as
![]() (46)
(46)
where use is made of the y-component of the gamma matrix four vector as given in Equation (17). Note that again the matrix ![]() plays the role of the imaginary unit i. We also have the property
plays the role of the imaginary unit i. We also have the property![]() . As a consequence, we can get the related
. As a consequence, we can get the related ![]() Majorana matrices by help of formula
Majorana matrices by help of formula
![]() (47)
(47)
Remember that ![]() commutes with the eight-dimensional gamma matrices, and therefore also with
commutes with the eight-dimensional gamma matrices, and therefore also with![]() . Moreover, the covariant derivate
. Moreover, the covariant derivate ![]() is not affected by a similarity transformation, which when being applied to the real Dirac Equation (16) then yields the eight-component real Majorana equation in the concise form
is not affected by a similarity transformation, which when being applied to the real Dirac Equation (16) then yields the eight-component real Majorana equation in the concise form
![]() (48)
(48)
which includes the coupling to the electromagnetic field via the matrix![]() , whereby gauge invariance is ensured as was discussed previously. The Majorana matrices attain, after some algebra, a simple block-diagonal form and read
, whereby gauge invariance is ensured as was discussed previously. The Majorana matrices attain, after some algebra, a simple block-diagonal form and read
![]() (49)
(49)
and the Majorana spinor field is connected to the Dirac spinor field by the transformation![]() . This can be written in terms of the real and imaginary part of the original Dirac spinor field
. This can be written in terms of the real and imaginary part of the original Dirac spinor field ![]() as follows
as follows
![]() (50)
(50)
Without an electromagnetic field for ![]() in (48), this Majorana equation is reducible and can be de- composed into two independent real four-component equations as presented before in the second section. The free spinor fields
in (48), this Majorana equation is reducible and can be de- composed into two independent real four-component equations as presented before in the second section. The free spinor fields ![]() and
and ![]() represent the electron and positron, which here are assembled in a charge doublet and become inextricably linked once an electromagnetic field is switched on. The real Majorana Equations (48)-(50) are fully equivalent to the complex standard Dirac Equation (12), and even appear to be more trans- parent than the equally valid real Dirac Equation (16).
represent the electron and positron, which here are assembled in a charge doublet and become inextricably linked once an electromagnetic field is switched on. The real Majorana Equations (48)-(50) are fully equivalent to the complex standard Dirac Equation (12), and even appear to be more trans- parent than the equally valid real Dirac Equation (16).
8. Conclusions
In this paper we have shown that the standard complex Dirac equation can be transformed into a real Dirac equation, which still permits the electromagnetic field to be introduced by minimal coupling, and which enables the real nature of that equation to be preserved in an eight-component spinor representation. This coupling to the electromagnetic field is established via the SO(2) symmetry group, which is equivalent to the U(1) symmetry of the complex Dirac equation. Thus the real Dirac equation also describes massive charged fermions coupled to an electromagnetic field. Coupling to other non-abelian gauge symmetry groups may also be possible, while pre- serving the real nature of that equation, if for the involved group use is made of its adjoint representation, which is purely imaginary and thus yields a real covariant derivative.
The real Dirac equation has a beta matrix that is antisymmetric, a property which causes problems for the fundamental Lorentz-invariant bilinear forms, such as ![]() which vanishes identically. This can only be re- medied by promoting the spinor field
which vanishes identically. This can only be re- medied by promoting the spinor field ![]() from a classical to a quantum field. A similar problem arises already in the complex Majorana equation, if it is derived from the standard Dirac equation [8] by requiring the spinor
from a classical to a quantum field. A similar problem arises already in the complex Majorana equation, if it is derived from the standard Dirac equation [8] by requiring the spinor ![]() be identical with its charge-conjugated version, which means
be identical with its charge-conjugated version, which means ![]() (see, e.g., [17] ). In this case the mass term in the resulting Lagrangian density also vanishes, unless anticommuting fermion fields are considered. So unlike the complex one, the real Dirac equation at the outset seems to make sense only as an equation for a quantum but not classical spinor field.
(see, e.g., [17] ). In this case the mass term in the resulting Lagrangian density also vanishes, unless anticommuting fermion fields are considered. So unlike the complex one, the real Dirac equation at the outset seems to make sense only as an equation for a quantum but not classical spinor field.
The real Dirac equation as here derived has essentially the same physical content as its complex ancestor, but looks somewhat cumbersome due to the larger gamma matrices involved. This is the mathematical price to be paid if complex numbers are fully avoided. The related Majorana version appears to be more transparent and seems easier to handle. The electromagnetic gauge field coupling in this equation is of matrix nature, as the imaginary unit is effectively replaced by the matrix![]() , being a generator of the SO(2) group of rotations in a plane. Thus the real Dirac equation is equivalent to the complex standard one which is more concise and con- venient. Yet there might be physical problems for which the real Dirac equation, in particular in its simpler Majorana version, will turn out to be advantageous.
, being a generator of the SO(2) group of rotations in a plane. Thus the real Dirac equation is equivalent to the complex standard one which is more concise and con- venient. Yet there might be physical problems for which the real Dirac equation, in particular in its simpler Majorana version, will turn out to be advantageous.
Acknowledgements
The author gratefully acknowledges the financial and institutional support provided for his work by the Extrater- restrial Physics Division headed by Robert Wimmer-Schweingruber at the Institute for Experimental and Ap- plied Physics of Kiel University in Germany.