1. Introduction
In this paper we explore the close and interesting relationship of a three-dimensional Euclidean Jordan algebra 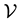 to the adjacency matrix of a strongly regular graph
to the adjacency matrix of a strongly regular graph . According to [1] , the Jordan algebras were formally introduced in 1934 by Pascual Jordan, John von Neumann and Eugene Wigner in [2] . There, the authors attempted to deduce some of the Hermitian matrix properties and they came across a structure lately called a Jordan algebra. Euclidean Jordan algebras were born by adding an inner product with a certain property to a Jordan algebra. It is remarkable that Euclidean Jordan algebras turned out to have such a wide range of applications. For instance, we may cite the application of this theory to statistics [3] , interior point methods [4] [5] and combinatorics [6] . More detailed literature on Euclidean Jordan algebras can be found in Koecher’s lecture notes [7] and in the monograph by Faraut and Korányi [8] .
. According to [1] , the Jordan algebras were formally introduced in 1934 by Pascual Jordan, John von Neumann and Eugene Wigner in [2] . There, the authors attempted to deduce some of the Hermitian matrix properties and they came across a structure lately called a Jordan algebra. Euclidean Jordan algebras were born by adding an inner product with a certain property to a Jordan algebra. It is remarkable that Euclidean Jordan algebras turned out to have such a wide range of applications. For instance, we may cite the application of this theory to statistics [3] , interior point methods [4] [5] and combinatorics [6] . More detailed literature on Euclidean Jordan algebras can be found in Koecher’s lecture notes [7] and in the monograph by Faraut and Korányi [8] .
Along this paper, we consider only simple graphs, i.e., graphs without loops and parallel edges, herein called graphs. Considering a graph X, we denote its vertex set by 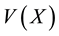 and its edge set by
and its edge set by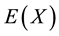 ―an edge whose endpoints are the vertices x and y is denoted by xy. In such case, the vertices x and y are adjacent or neighbors. The number of vertices of X,
―an edge whose endpoints are the vertices x and y is denoted by xy. In such case, the vertices x and y are adjacent or neighbors. The number of vertices of X,  , is called the order of X.
, is called the order of X.
A graph in which all pairs of vertices are adjacent (non-adjacent) is called a complete (null) graph. The number of neighbors of a vertex v in  is called the degree of v. If all vertices of a graph X have degree k, for some natural number k, then X is k-regular.
is called the degree of v. If all vertices of a graph X have degree k, for some natural number k, then X is k-regular.
We associate to X an n by n matrix , where each
, where each , if
, if , otherwise
, otherwise , called the adjacency matrix of X. The eigenvalues of A are simply called the eigenvalues of X.
, called the adjacency matrix of X. The eigenvalues of A are simply called the eigenvalues of X.
A non-null and not complete graph X is 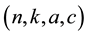 -strongly regular; if it is k-regular, each pair of adjacent vertices has a common neighbors and each pair of non-adjacent vertices has c common neighbors. The parameters of a
-strongly regular; if it is k-regular, each pair of adjacent vertices has a common neighbors and each pair of non-adjacent vertices has c common neighbors. The parameters of a  -strongly regular graph are not independent and are related by the equality
-strongly regular graph are not independent and are related by the equality
 (1)
(1)
It is also well known (see, for instance, [9] ) that the eigenvalues of a 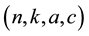 -strongly regular graph X are k,
-strongly regular graph X are k, 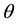 and
and , where
, where ![]() and
and ![]() are given by
are given by
![]() (2)
(2)
![]() (3)
(3)
Therefore, the usually called restricted eigenvalues ![]() and
and ![]() are such that the former is positive and the latter is negative. Their multiplicities can be obtained as follows (see, for instance, [10] ):
are such that the former is positive and the latter is negative. Their multiplicities can be obtained as follows (see, for instance, [10] ):
![]() (4)
(4)
![]() (5)
(5)
Taking into account the above eigenvalues and their multiplicities, the following additional conditions are widely used as feasible conditions for parameters sets ![]() of strongly regular graphs; that is, if
of strongly regular graphs; that is, if ![]() is a parameter set of a strongly regular graph, then the equality (1) and each one of the following inequalities holds:
is a parameter set of a strongly regular graph, then the equality (1) and each one of the following inequalities holds:
・ The nontrivial Krein conditions obtained in [11] :
![]() (6)
(6)
![]() (7)
(7)
・ The Seidel’s absolute bounds qre (see [12] ):
![]() (8)
(8)
With these conditions, many of the parameter sets are discarded as possible parameters sets of strongly regular graphs. To decide whether a set of parameters is the parameter set of a strongly regular graph is one of the main problems on the study of strongly regular graphs. It is worth noticing that these Krein conditions and the Seidel’s absolute bounds are special cases of general inequalities obtained for association schemes.
An association scheme with ![]() classes is a finite set S together with
classes is a finite set S together with ![]() relations
relations ![]() defined on S satisfying the following conditions.
defined on S satisfying the following conditions.
1) The set of relations ![]() is a partition of the Cartesian product of
is a partition of the Cartesian product of![]() .
.
2)![]() .
.
3) If![]() , then also
, then also![]() ,
, ![]() and for
and for![]() .
.
4) For each ![]() the number
the number ![]() of elements
of elements ![]() such that
such that ![]() and
and ![]() depends only from
depends only from![]() ,
, ![]() and
and![]() .
.
The numbers ![]() are called the intersection numbers of the association scheme. Some authors call this type of association schemes symmetric association schemes. The relations
are called the intersection numbers of the association scheme. Some authors call this type of association schemes symmetric association schemes. The relations ![]() of the association scheme can be re-
of the association scheme can be re-
presented by their adjacency matrices ![]() of order
of order ![]() defined by
defined by ![]() We may
We may
say that ![]() is the adjacency matrix of the graph
is the adjacency matrix of the graph![]() , with
, with ![]() and
and![]() . The Bose-Mesner algebra of the association scheme (introduced in [13] ) is defined, using these matrices, by the following conditions, which are equivalent to the conditions 1) - 4) of the association scheme:
. The Bose-Mesner algebra of the association scheme (introduced in [13] ) is defined, using these matrices, by the following conditions, which are equivalent to the conditions 1) - 4) of the association scheme:
1)![]() ,
,
2)![]() ,
,
3)![]() ,
,
4)![]() ,
,
where ![]() is the matrix of order n whose entries are equal to one and
is the matrix of order n whose entries are equal to one and ![]() is the identity matrix of order
is the identity matrix of order![]() . From 1) we may conclude that the matrices
. From 1) we may conclude that the matrices ![]() are linearly independent, and from 2) - 4) it follows that they generate a commutative
are linearly independent, and from 2) - 4) it follows that they generate a commutative ![]() -dimensional algebra
-dimensional algebra ![]() of symmetric matrices with constant diagonal. The matrices
of symmetric matrices with constant diagonal. The matrices ![]() commute and then, they can be diagonalized simultaneously, i.e., there exists a matrix
commute and then, they can be diagonalized simultaneously, i.e., there exists a matrix ![]() such that
such that![]() ,
, ![]() is a diagonal matrix. Thus, the algebra
is a diagonal matrix. Thus, the algebra ![]() is semisimple and has a unique complete system of
is semisimple and has a unique complete system of
orthogonal idempotents![]() . Therefore,
. Therefore, ![]() and
and![]() , where
, where ![]()
This paper is organized as follows. In Section 2, a short introduction on Euclidean Jordan algebras with the fundamental concepts is presented. In order to obtain new feasible conditions for the existence of a strongly regular graph, in Section 3, we define the generalized Krein parameters of a strongly regular graph. In Section 4, we establish some relations between the Krein parameters and the generalized Krein parameters, and present some properties of the generalized Krein parameters. Finally, since the generalized Krein parameters are nonnegative we establish new admissibility conditions, for the parameters of a strongly regular graph that give different information from that given by the Krein conditions 6) - 7).
2. Euclidean Jordan Algebras and Strongly Regular Graphs
In this section the main concepts of Euclidean Jordan Algebras that can be seen for instance in [8] , are shortly surveyed.
Let ![]() be a real vector space with finite dimension and a bilinear mapping
be a real vector space with finite dimension and a bilinear mapping ![]() from
from ![]() to
to![]() , that satisfies
, that satisfies![]() ,
,![]() . Then,
. Then, ![]() is called a real power associative algebra. If
is called a real power associative algebra. If ![]() contains an element, e, such that for all u in
contains an element, e, such that for all u in![]() ,
, ![]() , then e is called the unit element of
, then e is called the unit element of![]() . Considering a bilinear mapping
. Considering a bilinear mapping![]() , if for all
, if for all ![]() and
and ![]() in
in ![]() we have
we have ![]() and
and ![]()
![]() , with
, with![]() , then
, then ![]() is called a Jordan algebra. If
is called a Jordan algebra. If ![]() is a Jordan algebra with unit element, then
is a Jordan algebra with unit element, then ![]() is power associative (cf. [8] ). Given a Jordan algebra
is power associative (cf. [8] ). Given a Jordan algebra ![]() with unit element
with unit element![]() , if there is an inner product
, if there is an inner product ![]() that verifies the equality
that verifies the equality![]() , for any u, v, w in
, for any u, v, w in![]() , then
, then ![]() is called an Euclidean Jordan algebra. An element
is called an Euclidean Jordan algebra. An element ![]() in an Euclidean Jordan algebra
in an Euclidean Jordan algebra![]() , with unit element
, with unit element![]() , is an idempotent if
, is an idempotent if![]() . Two idempotents
. Two idempotents ![]() and
and ![]() are orthogonal if
are orthogonal if![]() . We call the set
. We call the set ![]() a complete system of orthogonal idempotents if (i)
a complete system of orthogonal idempotents if (i)![]() ,
,![]() ; (ii)
; (ii)![]() ,
, ![]() and (iii)
and (iii)![]() .
.
Let ![]() be an Euclidean Jordan algebra with unit element e. Then, for every u in
be an Euclidean Jordan algebra with unit element e. Then, for every u in![]() , there are unique distinct real numbers
, there are unique distinct real numbers![]() , and an unique complete system of orthogonal idempotents
, and an unique complete system of orthogonal idempotents ![]() such that
such that
![]() (9)
(9)
with![]() ,
, ![]() (see [8] , Theorem III 1.1). These
(see [8] , Theorem III 1.1). These![]() ’s are the eigenvalues of u and (9) is called the first spectral decomposition of u.
’s are the eigenvalues of u and (9) is called the first spectral decomposition of u.
The rank of an element u in ![]() is the least natural number k, such that the set
is the least natural number k, such that the set ![]() is linear dependent (where
is linear dependent (where![]() ), and we write
), and we write![]() . This concept is expanded by defining the rank of the algebra
. This concept is expanded by defining the rank of the algebra ![]() as the natural number
as the natural number![]() . The elements of
. The elements of ![]() with rank equal to the rank of
with rank equal to the rank of ![]() are the regular elements of
are the regular elements of![]() . This set of regular elements is open and dense in
. This set of regular elements is open and dense in![]() . If u is a regular element of
. If u is a regular element of![]() , with
, with![]() , then the set
, then the set ![]() is linearly dependent and the set
is linearly dependent and the set ![]() is linearly independent. Thus we may conclude that there exist unique real numbers
is linearly independent. Thus we may conclude that there exist unique real numbers![]() , such that
, such that![]() , where 0 is the null vector of
, where 0 is the null vector of![]() . Therefore, with the necessary adjustments, we obtain the following polynomial in
. Therefore, with the necessary adjustments, we obtain the following polynomial in![]() :
: ![]() This polynomial is called the characteristic polynomial of u, where each coefficient
This polynomial is called the characteristic polynomial of u, where each coefficient ![]() is a homogeneous polynomial of degree
is a homogeneous polynomial of degree ![]() in the coordinates of
in the coordinates of ![]() in a fixed basis of
in a fixed basis of![]() . Although we defined the characteristic polynomial for a regular element of
. Although we defined the characteristic polynomial for a regular element of![]() , we can extend this definition to all the elements in
, we can extend this definition to all the elements in![]() , because each polynomial
, because each polynomial ![]() is homogeneous and, as above referred, the set of regular elements of
is homogeneous and, as above referred, the set of regular elements of ![]() is dense in
is dense in![]() . The roots of the characteristic polynomial of
. The roots of the characteristic polynomial of![]() ,
, ![]() are called the eigenvalues of
are called the eigenvalues of![]() . Furthermore, the coefficients
. Furthermore, the coefficients ![]() and
and ![]() in the characteristic polynomial of u, are called the trace and the determinant of
in the characteristic polynomial of u, are called the trace and the determinant of![]() , respectively.
, respectively.
From now on, we consider the Euclidean Jordan algebra of real symmetric matrices of order![]() ,
, ![]() , such that
, such that![]() ,
, ![]() , where
, where ![]() is the usual product of matrices. Furthermore, the inner product of
is the usual product of matrices. Furthermore, the inner product of ![]() is defined as
is defined as![]() , where
, where ![]() is the classical trace of matrices, that is the sum of its eigenvalues.
is the classical trace of matrices, that is the sum of its eigenvalues.
Let ![]() be a
be a ![]() -strongly regular graph such that
-strongly regular graph such that![]() , and let
, and let ![]() be the adjacency matrix of
be the adjacency matrix of![]() . Then
. Then ![]() has three distinct eigenvalues, namely the degree of regularity
has three distinct eigenvalues, namely the degree of regularity![]() , and the restricted eigenvalues
, and the restricted eigenvalues ![]() and
and![]() , given in (2) and (3). Now we consider the Euclidean Jordan subalgebra of
, given in (2) and (3). Now we consider the Euclidean Jordan subalgebra of![]() ,
, ![]() , spanned by the identity matrix of order
, spanned by the identity matrix of order![]() ,
, ![]() , and the powers of
, and the powers of![]() . Since
. Since ![]() has three distinct eigenvalues, then
has three distinct eigenvalues, then ![]() is a three dimensional Euclidean Jordan algebra with
is a three dimensional Euclidean Jordan algebra with ![]() and
and ![]() is a basis of
is a basis of![]() .
.
Let ![]() be the unique complete system of orthogonal idempotents of
be the unique complete system of orthogonal idempotents of ![]() associated to
associated to![]() . Then
. Then
![]() (10)
(10)
where ![]() is the matrix whose entries are all equal to 1. Since
is the matrix whose entries are all equal to 1. Since ![]() is an Euclidean Jordan algebra that is closed for the Hadamard product of matrices, denoted by
is an Euclidean Jordan algebra that is closed for the Hadamard product of matrices, denoted by ![]() and
and ![]() is a basis of
is a basis of![]() , then there exist real numbers
, then there exist real numbers ![]() and
and![]() ,
, ![]() ,
, ![]() ,
, ![]() , such that
, such that
![]() (11)
(11)
The real numbers, defined in (11), (whose notation will be clarified later) ![]() and
and![]() ,
, ![]() ,
, ![]() ,
, ![]() , are called the “classical” Krein parameters of the graph
, are called the “classical” Krein parameters of the graph ![]() (cf. [10] ). Since
(cf. [10] ). Since ![]() and
and![]() , the “classical” Krein admissibility conditions
, the “classical” Krein admissibility conditions![]() , and
, and ![]() (presented in [9] , Theorem 21.3) can be deduced.
(presented in [9] , Theorem 21.3) can be deduced.
3. A Generalization of the Krein Parameters
Herein the generalized Krein parameters of a ![]() -strongly regular graph are defined and then, necessary conditions for the existence of a
-strongly regular graph are defined and then, necessary conditions for the existence of a ![]() -strongly regular graph are deduced. These conditions are generalizations of the Krein conditions (see Theorem 21.3 in [9] ). Throughout this paper we use a slight different notation from classical books like [9] [14] , because, in this way, the connections between the “classical’’ and the generalized parameters are better understood. Now we generalize the Krein parameters in order to obtain new generalized admissibility conditions on the parameters of strongly regular graphs. Firstly, considering
-strongly regular graph are deduced. These conditions are generalizations of the Krein conditions (see Theorem 21.3 in [9] ). Throughout this paper we use a slight different notation from classical books like [9] [14] , because, in this way, the connections between the “classical’’ and the generalized parameters are better understood. Now we generalize the Krein parameters in order to obtain new generalized admissibility conditions on the parameters of strongly regular graphs. Firstly, considering ![]() defined like in (10) in the Basis
defined like in (10) in the Basis![]() , and rewriting the idempotents under the new basis
, and rewriting the idempotents under the new basis ![]() of
of ![]() we obtain
we obtain
![]() (12)
(12)
Consider the natural number ![]() and denote by
and denote by ![]() the set of square matrices of order
the set of square matrices of order ![]() with real entries. Then for
with real entries. Then for![]() , we denote by
, we denote by ![]() and
and ![]() the Hadamard power of order
the Hadamard power of order ![]() of B and the Kronecker power of order
of B and the Kronecker power of order ![]() of
of![]() , respectively, with
, respectively, with ![]() and
and![]() .
.
Now, we introduce the following compact notation for the Hadamard and the Kronecker powers of the elements of S. Let x, y, z, ![]() ,
, ![]() and
and ![]() be natural numbers such that
be natural numbers such that![]() ,
, ![]() and
and![]() . Then we define
. Then we define
![]()
Again, since the Euclidean Jordan algebra ![]() is closed under the Hadamard product and
is closed under the Hadamard product and ![]() is a basis of
is a basis of![]() , then there exist real numbers
, then there exist real numbers![]() ,
, ![]() ,
, ![]() and
and![]() , such that
, such that
![]() (13)
(13)
We call the parameters ![]() and
and ![]() defined in (13) the generalized Krein parameters of the strongly re- gular graph
defined in (13) the generalized Krein parameters of the strongly re- gular graph![]() . Notice that
. Notice that ![]() and
and ![]() are precisely the Krein parameters of
are precisely the Krein parameters of ![]() already presented. With this notation, the Greek letters are used as idempotent indices and the Latin letters are used as exponents of Hadamard (Kronecker) powers.
already presented. With this notation, the Greek letters are used as idempotent indices and the Latin letters are used as exponents of Hadamard (Kronecker) powers.
4. Relations between the Krein Parameters and the Generalized Krein Parameters
In this section we prove that the generalized Krein parameters can be expressed in function of the Krein parameters. Before that, it is worth to mention that the previously introduced generalizations are straightforward extended to the Krein parameters of symmetric association schemes with ![]()
![]() classes, see [9] . Notice that the algebra spanned by the matrices of a symmetric association scheme with d classes is an Euclidean Jordan
classes, see [9] . Notice that the algebra spanned by the matrices of a symmetric association scheme with d classes is an Euclidean Jordan
Algebra with rank ![]() and with the Jordan product
and with the Jordan product ![]() where
where ![]() is the usual product of
is the usual product of
matrices. Furthermore, the inner product of ![]() is defined as
is defined as ![]() where
where ![]() is the classical trace of matrices, that is, the sum of its eigenvalues. Let us consider the matrices
is the classical trace of matrices, that is, the sum of its eigenvalues. Let us consider the matrices ![]() and
and ![]() of the Bose-Mesner algebra of an association scheme with
of the Bose-Mesner algebra of an association scheme with ![]() classes as defined in [14] . However, for convenience, we denote this
classes as defined in [14] . However, for convenience, we denote this
matrix ![]() such as defined in [14] by
such as defined in [14] by![]() . Therefore, we can say that
. Therefore, we can say that![]() , see [14] . Hence, we can say
, see [14] . Hence, we can say
that the matrices ![]() and
and ![]() satisfy,
satisfy,
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
The matrices ![]() and
and ![]() are usually called the eigenmatrix and the dual eigenmatrix of the association scheme, respectively.
are usually called the eigenmatrix and the dual eigenmatrix of the association scheme, respectively.
Theorem 1. Let ![]() be a
be a ![]() -strongly regular graph such that
-strongly regular graph such that ![]() whose adjacency matrix is
whose adjacency matrix is ![]() and has the eigenvalues
and has the eigenvalues ![]() and
and ![]() and whose eigenmatrix and dual eigenmatrix matrix are respectively
and whose eigenmatrix and dual eigenmatrix matrix are respectively ![]() and
and ![]() If
If ![]() and
and ![]() are natural numbers such that
are natural numbers such that ![]() then
then
![]() (18)
(18)
Proof. Consider that ![]() is the of idempotents defined in (12) and the following notation
is the of idempotents defined in (12) and the following notation![]() ,
, ![]() and
and ![]()
For ![]() since
since ![]() and
and![]() , it follows that
, it follows that ![]()
Therefore ![]() and since
and since ![]() implies
implies ![]() we obtain
we obtain
![]() (19)
(19)
Finally, from (19) the result follows.
Theorem 2. Let ![]() be a
be a ![]() -strongly regular graph such that
-strongly regular graph such that ![]() whose adjacency matrix is
whose adjacency matrix is ![]() and has the eigenvalues
and has the eigenvalues ![]() and
and ![]() and whose eigenmatrix and dual eigenmatrix matrix are respectively
and whose eigenmatrix and dual eigenmatrix matrix are respectively ![]() and
and ![]() Let
Let ![]() and
and ![]() be natural numbers such that
be natural numbers such that ![]() Then
Then
![]() (20)
(20)
Proof. Taking into account that ![]() and by the equalities (21) and (22)
and by the equalities (21) and (22)
![]() (21)
(21)
![]() (22)
(22)
we conclude that ![]() Therefore
Therefore ![]() and since by (22)
and since by (22)
![]() we obtain
we obtain![]() . Hence
. Hence ![]()
As an application of the Theorem 2 we may conclude that considering a strongly regular graph ![]() the generalized Krein parameters
the generalized Krein parameters ![]() can be expressed in function of the classical Krein parameters as follows:
can be expressed in function of the classical Krein parameters as follows:
![]() (23)
(23)
The expression (23) is obtained using (14) and (20). Summarizing, we have the following corollary.
Corollary 1. Let ![]() be a
be a ![]() -strongly regular graph such that
-strongly regular graph such that ![]() Then for all natural numbers
Then for all natural numbers ![]() and
and ![]() such that
such that ![]()
![]() (24)
(24)
Theorem 3. Let ![]() be a
be a ![]() -strongly regular graph such that
-strongly regular graph such that ![]() Then for all natural numbers
Then for all natural numbers ![]() and
and ![]() such that
such that ![]()
![]() (25)
(25)
Proof. We have ![]() Since from (21)
Since from (21) ![]() then
then
![]() . Hence we obtain
. Hence we obtain
![]()
Therefore, the equality (25) follows. ![]()
Recurring to (14) and (25), we may conclude the Corollary 2.
Corollary 2. Let ![]() be a
be a ![]() -strongly regular graph such that
-strongly regular graph such that ![]() Then for all natural numbers
Then for all natural numbers ![]() and
and ![]() such that
such that![]() ,
,
![]()
Theorem 4. Let ![]() be a
be a ![]() -strongly regular graph such that
-strongly regular graph such that ![]() Then
Then ![]() and
and ![]()
![]() (26)
(26)
Proof. We prove by induction on n. For ![]() the inequality (26) holds, since the classical Krein parameters
the inequality (26) holds, since the classical Krein parameters ![]() are nonnegative and
are nonnegative and ![]() Now assuming that the inequality (26) holds for
Now assuming that the inequality (26) holds for![]() , we prove that (26) also holds for
, we prove that (26) also holds for ![]() Consider the sum
Consider the sum ![]() Then from (14), we obtain
Then from (14), we obtain
![]()
Since for ![]() the inequality (26) is verified and the summands
the inequality (26) is verified and the summands ![]() are nonnegative, we may conclude that
are nonnegative, we may conclude that ![]()
![]()
Recurring to the Theorem 4 we are conducted to the Corollaries 3 and 4.
Corollary 3. Let G be a ![]() -strongly regular graph such that
-strongly regular graph such that ![]() Then for all natural numbers
Then for all natural numbers ![]() and
and ![]() such that
such that ![]() the generalized Krein parameters
the generalized Krein parameters ![]() are nonnegative.
are nonnegative.
Corollary 4. Let ![]() be a
be a ![]() -strongly regular graph such that
-strongly regular graph such that ![]() Then for all natural numbers
Then for all natural numbers ![]() and s such that
and s such that ![]() the generalized Krein parameters
the generalized Krein parameters ![]() are nonnegative.
are nonnegative.
Theorem 5. Let G be a strongly regular graph and let i, s and m be natural numbers such that ![]() Then
Then ![]()
Proof. Recurring to the inequalities (14)-(17) we have:
![]()
Theorem 6. Let G be a ![]() -strongly regular graph such that
-strongly regular graph such that![]() . Let
. Let ![]() and s be natural numbers such that
and s be natural numbers such that ![]() and
and ![]() Then the generalized Krein parameter
Then the generalized Krein parameter ![]() satisfy
satisfy ![]()
Proof. Similar to the Proof done in Theorem 5. ![]()
Let G be a ![]() -strongly regular graph such that
-strongly regular graph such that ![]() Since the generalized Krein parameters
Since the generalized Krein parameters ![]() and
and ![]() are nonnegative then we can establish new admissibility conditions distinct from the Krein conditions (6) and (7). For instance, the generalized Krein condition
are nonnegative then we can establish new admissibility conditions distinct from the Krein conditions (6) and (7). For instance, the generalized Krein condition ![]() allows us to establish a new theorem on strongly regular graphs after some algebraic manipulation of its expressions. Analyzing the generalized Krein parameter
allows us to establish a new theorem on strongly regular graphs after some algebraic manipulation of its expressions. Analyzing the generalized Krein parameter ![]() of a strongly regular graph with one in its spectra we deduce the following theorem (7).
of a strongly regular graph with one in its spectra we deduce the following theorem (7).
Theorem 7. Let ![]() be a
be a ![]() -strongly regular graph such that
-strongly regular graph such that ![]() whose adjacency matrix is
whose adjacency matrix is ![]() and has the eigenvalues
and has the eigenvalues ![]() and
and ![]() If
If ![]() then
then
![]() (27)
(27)
Proof. Since ![]() then we have
then we have
![]() (28)
(28)
From the inequality (28) and after some simplifications we conclude that
![]()
Therefore if ![]() then
then
![]()
Finally we have
![]() (29)
(29)
Dividing both members of (29) by ![]() we are supposing that
we are supposing that ![]() we obtain
we obtain
![]() (30)
(30)
![]()
1We must note that the equation ![]() as the roots
as the roots ![]() and the root
and the root ![]() Since
Since ![]() implies that
implies that ![]() and finally this implies that
and finally this implies that ![]() therefore
therefore ![]()
Now from the inequality (30) we conclude that if ![]() is a
is a ![]() -strongly regular graph with one in his
-strongly regular graph with one in his
spectra1 then ![]() implies that
implies that ![]()
We now present in Table 1 some examples of parameter sets ![]() that do not verify the inequality (27) of Theorem 7. We consider the parameter sets
that do not verify the inequality (27) of Theorem 7. We consider the parameter sets![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . For each example we present the respective eigen-
. For each example we present the respective eigen-
values![]() ,
, ![]() and the value of
and the value of ![]() defined by
defined by ![]()
5. Some Conclusions
In this paper, we have generalized the Krein parameters of a strongly regular graph and obtained some relations
between the classical Krein parameters and the generalized Krein parameters (see Corollaries 1 and 2). We also establish that these generalize Krein parameters are always positive and less than one (see Corollaries 3 and 4, and Theorems 5 and 6). Let ![]() and s be natural numbers such that
and s be natural numbers such that ![]() The generalized Krein admissibility conditions
The generalized Krein admissibility conditions ![]() with
with ![]() and
and ![]() with
with ![]() allow us to establish new admissibility conditions; they permit us to establish new inequalities on the parameters of a strongly regular graph. For instance the generalized Krein parameter condition
allow us to establish new admissibility conditions; they permit us to establish new inequalities on the parameters of a strongly regular graph. For instance the generalized Krein parameter condition ![]() after some algebraic manipulation allows us to establish the inequality (27) in Theorem 7. Finally, we conclude that we can extend the definition of generalized Krein parameters to a symmetric association scheme with
after some algebraic manipulation allows us to establish the inequality (27) in Theorem 7. Finally, we conclude that we can extend the definition of generalized Krein parameters to a symmetric association scheme with ![]() classes.
classes.
Acknowledgements
1) Luís Almeida Vieira was supported by the European Regional Development Fund through the program COMPETE and by the Portuguese Government through the FCT―Fundação para a Ciência e a Tecnologia under the project PEst―C/MAT/UI0144/2013.
2) Vasco Moço Mano was partially supported by Portuguese Funds trough CIDMA―Center for Research and development in Mathematics and Applications, Department of Mathematics, University of Aveiro, 3810-193, Aveiro, Portugal and the Portuguese Foundation for Science and Technology (FCT-Fundação para a Ciência e Tecnologia), within Project PEst-OE/MAT/UI4106/2014.
3) The authors would like to thank the anonymous referee for his/her careful revision and relevant comments that improved our paper.