Reduced Partition Function Ratio in the Frequency Complex Plane: A Mathematical Approach

Jie Yuan

Key Laboratory of Earth and Planetary Physics, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing, China.

DOI: 10.4236/ojg.2014.412049                

Abstract

This paper gives a mathematical approach to calculate the fractionation factor of isotopes in a general cluster (also known as super-molecule), which composes of necessary chemical effect within three bonds outside the interested atom(s). The cluster might have imaginary frequencies after being optimized in quantum softwares. The approach includes the contribution of the difference, which is resulted from the substitution of heavy and light isotopes in the cluster, of vibrations of imaginary frequencies to give precise prediction of isotope fractionation factor. We call the new mathematical approximation “reduced partition function ratio in the frequency complex plane (RPFR_C)”. If there is no imaginary frequency for a cluster, RPFR_C is simplified to be Urey (1947) or Bigeleisen and Mayer (1947) formula. Final results of this new algorithm are in good agreement with those in earlier studies.

Keywords

Isotope Fractionation, Cluster, Reduced Partition Function Ratio, Frequency Complex Plane

1. Introduction

In 1933, Urey and Rittenberg [1] pointed out that the isotopic fractionation factor in different systems could be calculated from spectroscopic data. A more convenient method for the calculation is known as Urey (1947) [2] or Bigeleisen and Mayer (1947) [3] model. This model needs only frequencies to calculate the factor by an equation namely “reduced isotopic partition function ratio (RPFR or β factor)”. However, a practical problem arises, when a cluster (cut from a big system; see details in Section 2.1) has some imaginary frequencies in the sets of vibrational frequencies [4] , RPFR cannot evaluate the isotope fractionation factor since it does not deal with imaginary frequencies (see details in Section 2.2).

To overcome this difficulty, Rustad et al. (2008) [4] applied the partial Hessian vibrational analysis (PHVA) [5] in the carbonate (e.g., calcite, aragonite and magnesite) clusters to predict the distributions of isotopes in these minerals; this operation neglects all imaginary frequencies (as well as some real ones) and then the remainder of real frequencies in the sets are used in RPFR, giving the carbon isotope fractionation factors in these minerals. But when using PHVA, also neglected is the contribution of the differences (due to the substitution of heavy and light isotopes in clusters) of imaginary frequencies to the isotope fractionation effect [6] . Therefore, previous problem is still under debate.

This study gives a new approach, i.e. reduced partition function ratio in the frequency complex plane (RPFR_C), to the calculation of isotope fractionations in general clusters. This new approach involves a more detailed physical figure of atom vibrations for the calculation than PHVA did; that is, the vibrations of all atoms due to the substitution of heavy and light isotopes in clusters are included to predict the isotope fractionations. This new approach is finally tested by studying isotope fractionation factors in liquid and mineral phases.

2. Theory

2.1. General Cluster for Isotope Research

We firstly give the theoretical background on building a general cluster for isotope research. The general cluster (Figure 1) includes three parts: A) interested isotopic atom(s) of an element at specific position; B) atoms linking three chemical bonds outside the interested atom(s). Stern and Wolfsberg (1966) [7] had theoretically proved that the biggest necessary influence of chemical effects on an interested isotope is within three bonds; and C) atoms to make the system to be converged in softwares. This kind of cluster could model isotope fractionations in both liquid and solid phases. In practical, researchers cut off atoms from a large periodical system to form solid-phase (e.g., calcite and aragonite in Ref. [4] ) clusters, and terminate the outside-broken bonds in part B with some hydrogen atoms in part C. For liquid phase, one adds few water molecules (and sometimes few ions [8] ) around the interested isotope to simulate its water environments; this technique is also called as “water-droplet” method [4] [9] [10] . For convenience, we represent the general cluster as a super-molecule XA_p, where A and X represent the interested atom and all atoms in parts of both B and C respectively and the subscript p the number of interested atoms of the same element in the center of the cluster (Figure 1(b)).

2.2. Harmonic Frequencies in Complex Plane

As discussed above, the super-molecule is sufficient to describe the chemical influence on isotopes at interested position; then one can use ab initio molecular orbital theory to get the frequencies. In Ref. [11] , mass-weighted

Figure 1. (a) 2-D schematic diagram of general cluster/super-molecule XA for isotope research. A represents the isotope locates at the interested position, i.e. the center of the cluster; X represents all atoms in B and C. (b) One more general cluster XA_p, with p interested atoms (A₁, A₂, ∙∙∙, A_p) in the center. See details in the text.

force constants are defined by

(1)

where is the mass of the kth atom in the molecule, and the force-constant is the second energy derivatives for coordinates and..And the kth normal-mode displacements has the form

(2)

where

(3)

in which are the eigenvalues of the matrix, and are the harmonic frequencies (Hz). This equation gives one set of frequencies for the heavy-isotope system and another for the light-isotope system; these two sets of frequencies are used to calculate the isotope fractionation factor.

The two sets of harmonic frequencies for a super-molecule would, however, sometimes have imaginary frequencies [12] . This is due to the fact that one cannot find a local minimal on the potential energy surface for all atoms of the cluster. And there will be some minus force constants in Equation (1). Upon taking the square root of the left hand side of Equation (3) for a minus mass-weighted force constant, a factor of complex unit will emerge, and there will be some imaginary frequencies for the molecule. Under this case, one cannot use RPFR to calculate the distribution of isotopes in the super-molecule, because only real frequencies are suitable for RPFR.

For a super-molecule, we suggest that all frequencies, especially the imaginary ones, should be included in the calculation of isotope fractionation. The reasons come from the following facts [11] : for a random frequency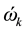, Equations (2) and (3) give the displacement (and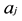) of each and every atom in the cluster. In other words, it gives a very important physical figure: all atoms in cluster will have a motion (with amplitude) for frequency. From this point of view, even an imaginary frequency has motions of all atoms in the molecule, and it will affect the difference of the isotope fractionation as vibrational contribution (see the next subsection).

In mathematics [13] , each set of frequencies has characteristic properties. The frequencies can be plotted on the complex plane (Figure 2), which is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis. For a general super-molecule, the eigenvalues of the mass-weighted matrix will have frequencies, which might include imaginary ones, 6 (5) (6, for nonlinear molecular, 5, for linear and diatom molecular) zeros (corresponding to translations and rotations), and real ones. All non-zero frequencies locate on those two axes, and the zeros at the origin. A real frequency equals its

own modulus, i.e.; and an imaginary one equals its own modulus multiplying the unit of complex number, i.e..

Figure 2. Plots of frequencies for one cluster/super-molecule on the complex plane.

2.3. Evaluation of Partition Function and Free Energy of the Super-Molecule

Based on the Born-Oppenheimer approximation (i.e. nearly harmonic approximation) [14] , the translational and rotational, and vibrational energies are the main contribution to the difference of isotope exchange reactions [2] [3] . The followings discuss the partition functions of these three kinds of energies and give the total free energy for the super-molecule.

The translational and rotational energies are in the form of and [15] , which are all real numbers. So the translational partition function for the super-molecule is

(4)

where is the volume of the cluster, is the mass of the cluster, is the Boltzmann constant, is the absolute temperature, is the Plank constant. And the rotational partition function is

(5)

for diatomic and linear molecules

(6)

for nonlinear molecules, where is the symmetry number of the molecule, and is the moment of inertia with respect to the appropriate principal axis.

The vibrational energy is in the form of (each); but the imaginary fre-

quencies cannot be included in this expression and the partition function in the classical mechanism [15] . However, as shown in previous subsection, this study needs to introduce the contribution of all imaginary frequencies into the partition function and free energy to calculate the isotope fractionation factor. Thus, only for isotope research in ab initio studies, we suggest the vibrational partition function of the super-molecule to be

(7)

where is the modulus of the kth frequency from Equation (3). If is real, is the vibrational partition function; and if is imaginary, is defined as imaginary-frequency correction to the vibrational partition function. Thus we call the imaginary-frequency-corrected vibrational partition function. Furthermore, the imaginary-frequency-corrected Helmholtz free energy of this super-molecule is given by

(8)

where is gas constant and

(9)

2.4. Teller-Redlich Product Rule in the Frequency Complex Plane

In Ref. [16] , Equation (3) can also be expressed as

(10)

where is the kinetic energy matrix, is the reciprocal mass of the kth atom in the molecule, is the force-constant matrix, and

(11)

Since will be identical for the molecule of different isotopes with the same method (i.e. the same exchange-correlation functional/basis set), now taking Equation (11) into Equation (10) gives

(12)

where the superscript “ ′ ” denotes the molecule with heavy isotopes.

Let us submit the frequencies with complex form. The number of complex unit is dependent on left hand side of Equation (3) and right hand side of Equation (1). Because, are real and nearly the same for one element, and the force constant matrix is identical for a cluster with given method, are the same in the numerator and denominator of Equation (12). We get

(13)

After the cancellation of, we have

(14)

Equation (14) is valid only when motions are vibrational normal modes. We consider those 6 (5) motions, corresponding to translational and rotational motions, convert of low frequency corresponding to weak forces. Then the ratio for the translational frequencies and rotation frequencies can be written as:

(15)

(16)

Submitting Equations (15) and (16) into Equation (14), we obtain the Teller-Redlich product rule in the frequency complex plane:

(17a)

for diatom and linear molecules and

(17b)

for nonlinear molecules.

3. Reduced Partition Function Ratio in Frequency Complex Plane

The differences for the isotopes in the super-molecule can be written as a typical chemical exchange reaction [2] [3] :

where and represent light and heavy isotope respectively, and is the number of interested atoms in the molecule.

The equilibrium constant for this reaction is given by

(18)

Because different isotopes have negligible difference of volume, isotope exchange reactions do not involve significant pressure-volume work [15] . The Gibbs free energy is equivalent to the Helmholtz free energy and we take Equation (8) into Equation (18), can be written as partition function ratio:

(19)

Let us substitute Equations (5)-(8) into Equation (19). For diatom and linear molecules, we have

(20a)

and for nonlinear molecules,

(20b)

where.

Equation (20) can be reduced to a more general expression by using Equation (17):

(21)

where RPFR_C is short for reduced partition function ratio in the frequency complex plane.

Obviously, one can see that if the super-molecule is at a local minimal on the potential energy surface (i.e.), all frequencies locate on the real-axis in the frequency complex plane (Figure 2). In such case, RPFR_C becomes Urey (1947) or Bigeleisen and Mayer (1947) formula. Due to the fact that the set of real numbers (i.e. frequencies here) is the subset of the set of the complex numbers [13] , the set of fractionation factors given by Urey (1947) or Bigeleisen and Mayer (1947) formula (i.e. RPFR) is the subset of the set of fractionation factors given by Equation (21) (i.e. RPFR_C) (Figure 3). In other words, this work extends Urey and Rittenberg’s (1933) idea [1] to focus on isotope fractionation research in the frequency complex plane.

The fractionation factor between two clusters can be written as:

(22)

(a) (b)

Figure 3. (a) The set of real numbers (i.e. frequencies here) is a subset of the set of the complex numbers; (b) The set of RFPR is a subset of the set of RPFR_C. The arrow indicates the process of the calculation of the isotope fractionation factors. Using real frequencies and imaginary ones in the calculations give RPFR and RPFR_C, respectively.

4. Tests of Present Approach

To understand the new algorithm, we compute RPFR_C and/or in typical isotope systems. Two examples are depicted below not for the accuracy prediction of experimental data, but for the abilities of our algorithm. All frequencies needed in RPFR_C are implemented in Gaussian09 [12] . The optimized geometries and frequencies for all examples are presented in the “Electronic supplementary materials”. Present RPFR_C and results are compared with corresponding references, i.e. those previously calculated from all real frequencies in published literatures. The difference (in ‰) between present result and the reference is in the form of

or.

1) The geranium isotope fractionation factor between (Figure 4(a)) and Ge(OH)₄-(H₂O)₃₀ (Figure 4(b)) (corresponding to _B and Ge(OH)₄-(H₂O)₃₀_D in Ref. [10] respectively) is a good example of study of isotopes in liquid phase. After optimized, each cluster has an imaginary frequency (Table 1). When calculating, Li et al. (2009) neglected the imaginary frequencies because 1) the main vibration vector of this imaginary frequency belongs to a water molecule located at outside of the super-molecule; 2) it is less than 50 cm⁻¹; and 3) RPFR is the same if they neglected it. The values of Li et al.’s αs at different temperatures are taken as references. As shown in Figure 5, the maximum difference be-

(a) (b)

Figure 4. Water-droplets for a), and b) Ge(OH)₄-(H₂O)₃₀ (cyan germanium, gray hydrogen, red oxygen). The optimized structures and frequencies are taken from Li et al. (2009).

Figure 5. ε α Ge(OH)₄-(H₂O)₃₀- versus T(K). The corresponding re- ference αs are from Li et al. (2009).

tween Li et al.’s and present results is 8.2 × 10⁻⁵‰ (273.15 K); this shows that present approach is very efficient to study isotope fractionation in liquids.

2) The carbon and ¹³C-¹⁸O clumped isotope fractionations in inner body of calcite are good examples of study of isotopes in solid phase. We cut a cluster (Figure 6) from the periodical calcite, of which the primitive cell parameters (Table 2) are calculated in CRYSTAL06 [17] , by the way published in Rustad et al. (2008). The

fitted polynomials of and K3866 in Ref. [18] are taken as references.

Results shown in Figures 7-9 indicate that our new algorithm have high accuracy. For in Figure 7, s are −10.2‰ (273.15 K) and −4.8‰ (273.15 K) for HF/3-21G/0.91 (the scaling factor) and B3LYP/6- 31G/0.97 [19] - [21] levels, respectively; and the difference of s between present results and data given by PHVA in Rustad et al. (2008) are −0.1‰ (=−4.1‰ - (−4‰), 298.15 K) and −3‰ (=−7‰ - (−4‰), 298.15 K) for HF/3-21G/0.91 and B3LYP/6-31G/0.97 levels, respectively. For K3866 in Figure 8 and Figure 9, s between present result and data given by Schauble et al. (2006) are 0.015‰ (273.15K) and −0.031‰ (273.15K) for HF/3-21G/0.91 and B3LYP/6-31G/0.97 levels, respectively. It seems clear that K3866 is not sensitive to the exchange-correlation functional/basis set/scaling factor, the number of imaginary frequency n and the magnitude of the frequencies (shown in Table 1 and the “Electronic supplementary materials”).

Table 1. Methods/basis_sets/scaling factors¹ used in Gaussian09 and the results of super-molecules.

¹http://cccbdb.nist.gov/. ²See Ref. [10] . n is the number of imaginary frequency. ^*The frequencies correspond to molecules with ⁷⁰Ge, ¹²C¹⁶O.

Table 2. Primitive cell parameter of calcite from CRYSTALL06, with B3LYP/(Ca_86-511d3G, C_6-21Gd, O_8-411d1)¹.

¹http://www.crystal.unito.it.

Figure 6. Cluster for calcite (dark gray―carbon, gray―hydrogen, red―oxygen, and yellow―calcium) extracted by the way in Rustad et al. (2008). The length of each O-H bond is 0.96 Å, and the charge of H is 0.333.

Figure 7. εversus T(K). The reference s are from Schauble et al. (2006).

Figure 8. Comparison of K3866s versus T(K). Present K3866s are given by Equation (21) at HF/ 321G/0.91 (dots) and B3LYP/631G/0.97 (solid) levels. Schauble et al.’s (2006) K3866s (bold solid) are given by lattice dynamics.

Figure 9. ε K3866 versus T(K). The reference K3866 is from Schauble et al. (2006).

5. Conclusion

For a general cluster for isotope research (defined in Section 2.1), we have a new Equation (21) to calculate the isotope fractionation factor in the cluster. The calculation based on this equation has a clearer background of physical mechanism, which includes the contribution of vibrations of all atoms to the factor, than that based on PHVA. If there is no imaginary frequencies for the cluster, Equation (21) is simplified to be the Urey (1947) or Bigeleisen and Mayer (1947) formula. The examples show that our new algorithm is valid and efficient with high accuracy. Although the accuracy is mathematically high, we again address that present approach should be only used to calculate the isotope fractionation factor.

Acknowledgements

The author is grateful to Dr. Zhang Zhigang in IGGCAS for helpful discussions. All of the calculations are performed at the IGGCAS computer simulation lab. This work is supported by the National Natural Science Foundation of China (Grant No. 41303047, 41020134003 and 90914010).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Urey, H.C. and Rittenberg, D. (1933) Some Thermodynamic Properties of the H1H2, H2H2 Molecules and Compounds Containing the H2 Atom. Journal of Chemical Physics, 1, 137-143. http://dx.doi.org/10.1063/1.1749265
[2]	Urey, H.C. (1947) The Thermodynamic Properties of Isotopic Substances. The Journal of the Chemical Society, 562- 581. http://pubs.rsc.org/en/Content/ArticleLanding/1947/JR/jr9470000562
[3]	Bigeleisen, J. and Mayer, M.G. (1947) Calculation of Equilibrium Constants for Isotopic Exchange Reactions. Journal of Chemical Physics, 15, 261-267. http://dx.doi.org/10.1063/1.1746492 Rustad, J.R., Nelmes, S.L., Jackson, V.E. and Dixon, D.A. (2008) Quantum-Chemical Calculations of Carbon-Isotope Fractionation in CO2 (g), Aqueous Carbonate Species, and Carbonate Minerals. The Journal of Physical Chemistry A, 112, 542-555. http://dx.doi.org/10.1021/jp076103m http://www.ncbi.nlm.nih.gov/pubmed/18166027
[4]	Li, H. and Jensen, J.H (2002) Partial Hessian Vibrational Analysis: The Localization of the Molecular Vibrational Energy and Entropy. Theoretical Chemistry Accounts, 107, 211-219. http://dx.doi.org/10.1007/s00214-001-0317-7
[5]	Yuan, J. and Liu, Y. (2011) An Important Method for Calculating Isotope Fractionation in the Solid State Partial Hessian Vibrational Analysis (PHVA). Bulletin of Mineralogy, Petrology and Geochemistry, 30, 472-476.
[6]	Stern, M.J. and Wolfsber, M. (1966) Simplified Procedure for Theoretical Calculation of Isotope Effects Involving Large Molecules. The Journal of Chemical Physics, 45, 4105. http://dx.doi.org/10.1063/1.1727463
[7]	Driesner, T., Ha, T.K. and Seward, T.M (2000) Oxygen and Hydrogen Isotope Fractionation by Hydration Complexes of Li+, Na+, K+, Mg2+, F?, Cl?, and Br?: A Theoretical Study. Geochimica et Cosmochimica Acta, 64, 3007-3033. http://dx.doi.org/10.1016/S0016-7037(00)00407-5
[8]	Liu, Y. and Tossell, J.A. (2005) Ab Initio Molecular Orbital Calculations for Boron Isotope Fractionations on Boric Acids and Borates. Geochimica et Cosmochimica Acta, 69, 3995-4006. http://dx.doi.org/10.1016/j.gca.2005.04.009
[9]	Li, X.F., Zhao, H., Tang, M. and Liu, Y. (2009) Theoretical Prediction for Several Important Equilibrium Ge Isotope Fractionation Factors and Geological Implications. Earth and Planetary Science Letters, 287, 1-11. http://dx.doi.org/10.1016/j.epsl.2009.07.027
[10]	Pople, J.A., Schlegel, H.B., Krishnan, R., Defrees, D.J., Binkley, J.S., Frisch, M.J., Whiteside, R.A., Hout, R.F. and Hehre, W.J. (1981) Molecular-Orbital Studies of Vibrational Frequencies. International Journal of Quantum Chemistry, 20, 269-278. http://dx.doi.org/10.1002/qua.560200829
[11]	Frisch, M.J., Trucks, G.W., Schlegel, H.B., Scuseria, G.E., Robb, M.A., Cheeseman, J.R., Montgomery, J.J.A., Vreven, T., Kudin, K.N., Burant, J.C., Millam, J.M., Iyengar, S.S., Tomasi, J., Barone, V., Mennucci, B., Cossi, M., Scalmani, G., Rega, N., Petersson, G.A., Nakatsuji, H., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Klene, M., Li, X., Knox, J.E., Hratchian, H.P., Cross, J.B., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R.E., Yazyev, O., Austin, A.J., Cammi, R., Pomelli, C., Ochterski, J.W., Ayala, P.Y., Morokuma, K., Voth, G.A., Salvador, P., Dannenberg, J.J., Zakrzewski, V.G., Dapprich, S., Daniels, A.D., Strain, M.C., Farkas, O., Malick, D.K., Rabuck, A.D., Raghavachari, K., Foresman, J.B., Ortiz, J.V., Cui, Q., Baboul, A.G., Clifford, S., Cioslowski, J., Stefanov, B.B., Liu, G., Liashenko, A., Piskorz, P., Komaromi, I., Martin, R.L., Fox, D.J., Keith, T., Al-Laham, M.A., Peng, C.Y., Nanayakkara, A., Challacombe, M., Gill, P.M.W., Johnson, B., Chen, W., Wong, M.W., Gonzalez, C. and Pople, J.A. (2009) Gaussian 09, Revision A.01. Gaussian, Inc., Wallingford.
[12]	Fong, C.F.C.M., Kee, D.D. and Kaloni, P.N. (2002) Advanced Mathematics for Engineering and Science. World Scientific Publishing Co. Pte. Ltd., Singapore.
[13]	Born, M. and Oppenheimer, R. (1927) On the Quantum Theory of Molecules. Annalen der Physik, 84, 457-484. http://dx.doi.org/10.1002/andp.19273892002
[14]	Levine, I.N. (1995) Physical Chemistry. 4th Edition, McGraw-Hill, Inc., New York.
[15]	Wilson, E.B.J., Decius, J.C. and Cross, P.C. (1955) Molecular Vibrations: The Theory of Infrared and Raman Spectra. Dover Publications, New York.
[16]	Dovesi, R., Saunders, V.R., Roetti, C., Orlando, R., Zicovich-Wilson, C.M., Pascale, F., Civalleri, B., Doll, K., Harrison, N.M., Bush, I.J., D’Arco, P. and Llunell, M. (2006) CRYSTAL06 User’s Manual. University of Torino, Torino.
[17]	Schauble, E.A., Ghosh, P. and Eiler, J.M. (2006) Preferential Formation of 13C-18O Bonds in Carbonate Minerals, Estimated Using First-Principles Lattice Dynamics. Geochimica et Cosmochimica Acta, 70, 2510-2529. http://dx.doi.org/10.1016/j.gca.2006.02.011
[18]	Becke, A.D. (1993) Density-Functional Thermochemistry. III. The Role of Exact Exchange. Journal of Chemical Physics, 98, 5648-5652. http://dx.doi.org/10.1063/1.464913
[19]	Lee, C.T., Yang, W.T. and Parr, R.G. (1988) Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron-Density. Physical Review B, 37, 785-789. http://dx.doi.org/10.1103/PhysRevB.37.785
[20]	Vosko, S.H., Wilk, L. and Nusair, M. (1980) Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin-Density Calculations—A Critical Analysis. Canadian Journal of Physics, 58, 1200-1211. http://dx.doi.org/10.1139/p80-159
[21]	Stephens, P.J., Devlin, F.J., Chabalowski, C.F. and Frisch, M.J. (1994) Ab Initio Calculation of Vibrational Absorption and Circular-Dichroism Spectra Using Density-Functional Force-Fields. Journal of Physical Chemistry, 98, 11623-11627. http://dx.doi.org/10.1021/j100096a001