Erratum to “Weierstrass’ Elliptic Function Solution to the Autonomous Limit of the String Equation of Type (2,5)” [Advances in Pure Mathematics 4 (2014), 494-497] ()
Abstract
In this note, we analyze a few major claims about . As a consequence, we rewrite a major theorem, nullify its proof and one remark of importance, and offer a valid proof for it. The most important gift of this paper is probably the reasoning involved in all: We observe that a constant, namely t, has been changed into a variable, and we then tell why such a move could not have been made, we observe the discrepancy between the claimed domain and the actual domain of a supposed function that is created and we then explain why such a function could not, or should not, have been created, along with others.
P. 494, L. 7-: The string equation of type (q, p) should be correctly read as
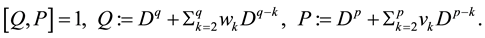
P. 496, L. 13 - 14: Theorem B should be correctly read as follows:
Theorem B. The autonomous limit Equation (A) has a solution concretely described by the Weierstrass’ elliptic function as
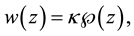
where  or 3.
or 3.
P. 496, L. 17: In Remark, g2 and g3 in the elliptic function theory should be correctly read as follows:
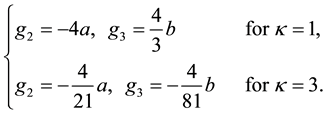
P. 496, L. 21: In the r.h.s. of Equation (1), “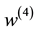 ” should be correctly read as “
” should be correctly read as “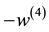 ”.
”.
P. 496, L. 3- - P. 497, L. 2: These 5 lines should be correctly read as follows:
If both of (2) and (3) are valid, then 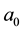 must vanish and
must vanish and 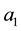 coincides with 4 or
coincides with 4 or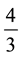 .
.
Case  and
and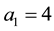 : In this case, we immediately obtain
: In this case, we immediately obtain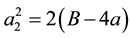 ,
, 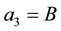 ,
,
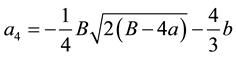 , where
, where 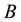 is a root of
is a root of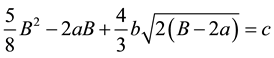 . Inversely, if these are sa-
. Inversely, if these are sa-
tisfied, both of (2) and (3) are valid. 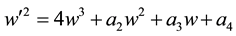 can be reduced to
can be reduced to ![]() by
by
![]() . But, for brevity, now we put
. But, for brevity, now we put![]() , and then
, and then![]() ,
, ![]() , i.e.
, i.e.
![]() . Here
. Here ![]() and
and![]() . The irrational equation satisfied by
. The irrational equation satisfied by ![]() determines the
determines the
integral constant ![]() in the r.h.s. of (2) as
in the r.h.s. of (2) as![]() .
.
Case ![]() and
and![]() : In this case, we easily obtain
: In this case, we easily obtain![]() ,
, ![]() ,
,![]() . Only
. Only ![]() is
is
allowed as the integral constant c in the r.h.s. of (2). Inversely, if these are satisfied, both of (2) and (3) are valid.
![]() is reduced to
is reduced to ![]() by w = 3v, and then
by w = 3v, and then ![]() and
and![]() . □
. □