Consider the following control problem containing support functions introduced by Husain et al. [1]
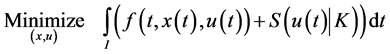
subject to
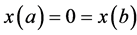 (1)
(1)
 (2)
(2)
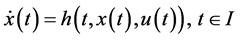 (3)
(3)
where
1) 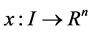 is a differentiable state vector function with its derivative
is a differentiable state vector function with its derivative 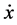 and
and 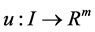 is a smooth control vector function.
is a smooth control vector function.
2) 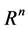 denotes an n-dimensional Euclidean space and
denotes an n-dimensional Euclidean space and 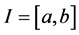 is a real interval.
is a real interval.
3) ,
, 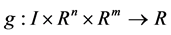 and
and 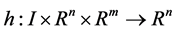 are continuously differentiable.
are continuously differentiable.
4)  and
and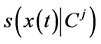 ,
, 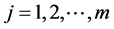 are the support function of the compact set K and
are the support function of the compact set K and  respectively.
respectively.
Denote the partial derivatives of f where by ft, fx and ft,
![]()
where superscript denote the vector components. Similarly we have ht, hx, hu and gt, gx, gu. X is the space of continuously differentiable state functions![]() . Such that
. Such that ![]() and
and ![]() and are equipped with
and are equipped with
the norm ![]() and U, the space of piecewise continuous control vector functions
and U, the space of piecewise continuous control vector functions ![]()
having the uniform norm ![]() The differential Equation (2) with initial conditions expressed as
The differential Equation (2) with initial conditions expressed as
![]() may be written as
may be written as ![]() where
where
![]() being the space of continuous function from I to Rn defined as
being the space of continuous function from I to Rn defined as ![]() In the derivation of these optimality condition, some constraint qualification to make the equality constraint locally solvable [2] and hence the Fréchét derivative of
In the derivation of these optimality condition, some constraint qualification to make the equality constraint locally solvable [2] and hence the Fréchét derivative of ![]() (say) with respect to
(say) with respect to ![]() namely
namely ![]() are required to be surjective. In [1] , Husain et al. derived the following Fritz john type necessary optimality for the existence of optimal solution of (CP).
are required to be surjective. In [1] , Husain et al. derived the following Fritz john type necessary optimality for the existence of optimal solution of (CP).
Proposition 1. (Fritz John Condition): If ![]() is an optimal solution of (CP) and the Fréchét derivative Q' is surjective, then there exist Langrange multipliers
is an optimal solution of (CP) and the Fréchét derivative Q' is surjective, then there exist Langrange multipliers ![]() and piecewise smooth
and piecewise smooth![]() ,
, ![]() ,
, ![]() and
and ![]() such that for all t,
such that for all t,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
As in [3] , Husain et al. [1] pointed out if the optimal solution for (CP) is normal, then the Fritz john type optimal conditions reduce to the following Karush-Kuhn-Tucker optimal conditions.
Proposition 2. If ![]() is an optimal solution and is normal and Q' is surjective, there exist piecewise smooth
is an optimal solution and is normal and Q' is surjective, there exist piecewise smooth ![]() with
with![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() such that
such that
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
Using the Karush-Kuhn-Tucker type optimality condition given in Proposition 2, Husain et al. [1] presented the following Wolfe type dual to the control problem (CP) and proved usual duality theorem under the pseudo-
convexity of ![]() for all
for all![]() , and
, and![]() ,
,![]() .
.
(WCD): Maximize
![]()
subject to
![]()
![]()
![]()
![]()
![]()
We review some well known facts about a support function for easy reference. Let ![]() be a compact convex set in
be a compact convex set in![]() . Then the support function of
. Then the support function of ![]() denoted by
denoted by ![]() is defined as
is defined as
![]()
A support function, being convex and everywhere finite, has a subdifferential in the sense of convex analysis, that is, there exists ![]() such that
such that ![]() for all x. The subdif-
for all x. The subdif-
ferential of ![]() is given by
is given by ![]() Let
Let ![]() be normal
be normal
cone at a point ![]() Then
Then ![]() if and only if
if and only if ![]() or, equivalently,
or, equivalently, ![]() is in the subdifferential of s at
is in the subdifferential of s at ![]()
In order to relax the pseudoconvexity in [1] , Mond-Weir type dual to (CP) is constructed and various duality theorems are derived. Particular cases are deduced and it is also indicated that our results can be considered as the dynamic generalization of the duality results for nonlinear programming problem with support functions.
2. Mond-Weir Type Duality
We propose the following Mond-Weir type dual (M-WCD) to the control problem (CP):
Dual (M-WCD): Maximize ![]()
subject to
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
Theorem 1. (Weak Duality): Assume that
(A1): ![]() is feasible for (CP),
is feasible for (CP),
(A2): ![]() is feasible for the problem (M-WCD),
is feasible for the problem (M-WCD),
(A3): ![]() for
for ![]() is pseudoconvex, and
is pseudoconvex, and
(A4): ![]() for all
for all ![]() and
and ![]() are quasiconvex at
are quasiconvex at ![]()
Then
![]()
Proof: Since ![]() we have
we have
![]()
and
![]()
Combining these inequalities with (14) and (15) respectively, we have
![]()
and
![]()
These, because of the hypothesis (A4) yields
![]() (19)
(19)
![]() (20)
(20)
Combining (19) and (20) and then using (12) and (13), we have
![]()
This, due to the pseudoconvexity of ![]() for
for ![]() implies
implies
![]()
Since ![]() the above inequality gives
the above inequality gives
![]()
yielding
![]()
Theorem 2. (Strong Duality): If ![]() is an optimal solution of (CP) and is normal, then there exist piecewise smooth
is an optimal solution of (CP) and is normal, then there exist piecewise smooth ![]() with
with ![]()
![]() and such that
and such that ![]() is feasible for (M-WCD) and the corresponding values of (CP) and (M-WCD) are equal. If also, the hypotheses of Theorem 1 hold, then
is feasible for (M-WCD) and the corresponding values of (CP) and (M-WCD) are equal. If also, the hypotheses of Theorem 1 hold, then ![]() is optimal solution of the problem (M-WCD).
is optimal solution of the problem (M-WCD).
Proof: Since ![]() is an optimal solution of (CP) and is normal, it follows by Proposition 2 that there exist piecewise smooth
is an optimal solution of (CP) and is normal, it follows by Proposition 2 that there exist piecewise smooth ![]()
![]()
![]()
![]() and
and![]() . satisfying for all
. satisfying for all ![]() the conditions (4)-(10) are satisfied. The conditions (4)-(6) together with (9) and (10) imply that
the conditions (4)-(10) are satisfied. The conditions (4)-(6) together with (9) and (10) imply that ![]() is feasible for (M-WCD). Using
is feasible for (M-WCD). Using ![]() we obtain,
we obtain,
![]()
The equality of the objective functionals of the problems (CP) and (M-WCD) follows. This along with the hypotheses of Theorem 1, the optimality of ![]() for (M-WCD) follows.
for (M-WCD) follows.
The following gives the Mangasarian type strict converse duality theorem:
Theorem 3. (Strict Converse Duality): Assume that
(A1): ![]() is an optimality solution of (CP) and is normal;
is an optimality solution of (CP) and is normal;
(A2): ![]() is an optimal solution of (M-WCD),
is an optimal solution of (M-WCD),
(A3): ![]() in strictly is pseudoconvex for all
in strictly is pseudoconvex for all ![]() and
and
(A4): ![]() for all
for all ![]() and
and ![]() are quasi convex.
are quasi convex.
Then ![]() i.e.
i.e. ![]() is an optimal solution of (CP).
is an optimal solution of (CP).
Proof: Assume that ![]() and exhibit a contradiction. Since
and exhibit a contradiction. Since ![]() is an optimality solution of
is an optimality solution of
(CP). By Theorem 2 there exist ![]() with
with ![]() such that
such that
![]() is an optimal solution of (M-WCD).
is an optimal solution of (M-WCD).
Thus
![]() (21)
(21)
Since ![]() is feasible for (CP) and
is feasible for (CP) and ![]() for (M-WCD), we have
for (M-WCD), we have
![]()
and
![]()
These, because of the hypothesis (A4) imply the merged inequality
![]()
This, by using the equality constraints (12) and (13) of (M-WCD) gives
![]()
By the hypothesis (A2), this implies
![]()
(using (21)). Consequently, we have
![]()
Since ![]() for
for ![]() and
and ![]() for
for ![]() this yields,
this yields,
![]()
This cannot happen. Hence ![]()
3. Converse Duality
The problem (M-WCD) can be written as the follows:
Maximize: ![]()
subject to
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
where
![]()
![]()
Consider ![]() and
and ![]() as defining a map- pings
as defining a map- pings ![]() and
and ![]() respectively where
respectively where ![]() is the space of piecewise smooth
is the space of piecewise smooth![]() , V is space of piececewise smooth
, V is space of piececewise smooth![]() , Wj is the space of piecewise of smooth Wj,
, Wj is the space of piecewise of smooth Wj, ![]() B1 and B2 are Banach spaces.
B1 and B2 are Banach spaces. ![]() and
and ![]() with
with ![]() Here some restrictions are required on the equality constraints. For this, it suffices that if the
Here some restrictions are required on the equality constraints. For this, it suffices that if the ![]() derivatives
derivatives ![]() and
and
![]() have weak * closed range.
have weak * closed range.
Theorem 4. (Converse Duality): Assume that
(A1): ![]() and h are twice continuously differentiable.
and h are twice continuously differentiable.
(A2): ![]() is an optimal solution of (CP).
is an optimal solution of (CP).
(A3): ![]() and
and ![]() have weak * closed ranges.
have weak * closed ranges.
(A4): ![]()
![]() for some
for some![]() , and
, and
![]()
(A5): 1) The gradient vectors ![]() and
and ![]() are linearly independent, or
are linearly independent, or
2) The gradient vectors ![]() and
and ![]() are linearly independent.
are linearly independent.
(A6): ![]()
Proof: Since ![]() is an optimal solution of (M-WCD), by Proposition 1 there exists
is an optimal solution of (M-WCD), by Proposition 1 there exists ![]()
![]() and
and ![]() and piecewise smooth functions
and piecewise smooth functions ![]()
![]()
![]() ,
, ![]() , such that
, such that
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
Multiplying (24) by ![]() and summing over i and then integrating using (28), we have
and summing over i and then integrating using (28), we have
![]()
which can be written as,
![]() (33)
(33)
Multiplying (25) by ![]() and then integrating and using (29), we have
and then integrating and using (29), we have
![]()
This implies
![]()
or
![]() (34)
(34)
Using the equality constraints (12) and (13) of the problem (M-WCD) in (22) and (23), we have
![]() (35)
(35)
![]() (36)
(36)
Combining (35) and (36), we have
![]()
This by premultiplying by ![]() and then integrating, we have
and then integrating, we have
![]()
Using (33) and (34), we have
![]()
This because of hypothesis (A4) implies
![]()
Using ![]() gives
gives
![]()
This, because of hypothesis (A5) implies
![]() (37)
(37)
Assume ![]() (37) gives
(37) gives ![]() from (24) it follows
from (24) it follows ![]() Consequently we have
Consequently we have
![]()
contradicting (32). Hence ![]() and
and ![]() The relations (26) and (27) gives
The relations (26) and (27) gives
![]() and
and ![]()
yielding ![]() and
and![]() .
.
From (24), we have
![]() (38)
(38)
and
![]() (39)
(39)
From (25), we have
![]() (40)
(40)
and
![]() (41)
(41)
The feasibility of ![]() for (CP) follows from (38) and (40).
for (CP) follows from (38) and (40).
Consider
![]()
(by using ![]() along (39) and (41)).
along (39) and (41)).
This along with the generalized convexity hypotheses implies that ![]() is an optimal solution of (M-WCD).
is an optimal solution of (M-WCD).
4. Special Cases
Let for ![]()
![]() and
and ![]() be positive semidefinite matrices and continuous on I. Then
be positive semidefinite matrices and continuous on I. Then
![]()
where
![]()
and
![]()
where
![]()
Replacing the support function by their corresponding square root of a quadratic form, we have:
Primal (CP0): Minimize ![]()
subject to
![]()
![]()
![]()
(M-WCD0): Maximize ![]()
subject to
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The above pair of nondifferentiable dual control problem has not been explicitly reported in the literature but the duality amongst (CP0) and (M-WCD0) readily follows on the lines of the analysis of the preceding section.
5. Related Nonlinear Programming Problems
If the time dependency of the problem (CP) and (M-WCD) is removed, then these problems reduce to the following problem (NP), its Mond-Weir dual (M-WND):
Primal (NP0): Minimize ![]()
subject to
![]()
![]()
Dual (M-WND0): Maximize ![]()
subject to
![]()
![]()
![]()
![]()
![]()
![]()
The above nonlinear programming problems with support functions do not appear in the literature. However, if ![]() and
and ![]() are replaced by
are replaced by ![]() and
and ![]() respectively in (NP0), then problems reduced to following studied by Hussain et al. [4] .
respectively in (NP0), then problems reduced to following studied by Hussain et al. [4] .
(P1): Minimize ![]()
subject to
![]()
(M-WCD): Maximize ![]()
subject to
![]()
![]()
![]()
6. Conclusion
Mond-Weir type duality for a control problem having support functions is studied under generalized convexity assumptions. Special cases are deduced. The linkage between the results of this research and those of nonlinear programming problem with support functions is indicated. The problem of this research can be revisited in multiobjective setting.