1. Introduction
Analysis of transactional data has been considered as an important data mining problem. Market basket data is an example of such transactional data. In a market-basket data set, each transaction is a collection of items bought by a customer at one time. The concept proposed in [1] is to find the co-occurrence of items in transactions, given minimum support and minimum confidence thresholds. Temporal Association rule mining is an important extension of above-mentioned problem. When an item from super-market is bought by a customer, this is called transaction and its time is automatically recorded. Ale et al. [2] have proposed a method of extracting association rules that hold within the life-span of the corresponding item set.
Mahanta et al. [3] have introduced concept of locally frequent item sets as item sets that are frequent in certain time intervals and may or may not be frequent throughout the life-span of the item set. An efficient algorithm is developed by them which is used find such item sets along with a list of sequences of time intervals. Considering the time-stamp as calendar dates, a method is discussed in [4] which can extract yearly, monthly and daily periodic or partially periodic patterns. If the periods are kept in a compact manner using the method discussed in [4] , it turns out to be a fuzzy time interval. In this paper, we discuss such patterns and device algorithms for extracting such patterns. Although our algorithm works for extracting monthly fuzzy patterns, it can be modified for daily fuzzy periodic patterns. The paper is organized as follows. In Section 2, we discuss related works. In Section 3, we discuss terms, definitions and notations used in the algorithm. In Section 4, the proposed algorithm is discussed. In Section 5, we discuss about results and analysis. Finally a summary and lines for future works are discussed in Section 6.
2. Related Works
Agrawal et al. [1] first formulated association rules mining problems. One important extension of this problem is Temporal Data Mining [5] by taking into account the time aspect, more interesting patterns that are time dependent can be extracted. The problems associated are to find valid time periods during which association rules hold and the discovery of possible periodicities that association rules have. In [2] , an algorithm for finding temporal rules is described. There each rule has associated with it a time frame. In [3] , the works done in [2] has been extended by considering time gap between two consecutive transactions containing an item set into account.
Considering the periodic nature of patterns, Ozden et al. [6] proposed a method, which is able to find patterns having periodic nature where the period has to be specified by the user. In [7] , Li et al. discuss about a method of extracting temporal association rules with respect to fuzzy match, i.e. association rule holding during “enough” number of intervals given by the corresponding calendar pattern. Similar works were done in [8] incorporating multiple granularities of time intervals (e.g. first working day of every month) from which both cyclic and user defined calendar patterns can be achieved.
Mining fuzzy patterns from datasets have been studied by different authors. In [9] , the authors present an algorithm for mining fuzzy temporal patterns from a given process instance. Similar work is done in [10] . In [11] method of extracting fuzzy periodic association rules is discussed.
3. Terms, Definitions and Notations Used
Let us review some definitions and notations used in this paper.
A fuzzy number is a convex normalized fuzzy set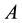 
defined on the real line 
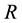such that
1) there exists an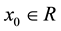 
such that
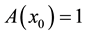, and
2) 
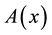is piecewise continuous.
Thus a fuzzy number can be thought of as containing the real numbers within some interval to varying degrees.
Fuzzy intervals are special fuzzy numbers satisfying the followings:
1) There exists an interval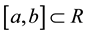 
such that 
for all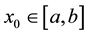
, and
2) 
is piecewise continuous.
A fuzzy interval can be thought of as a fuzzy number with a flat region. A fuzzy interval 
is denoted by 
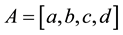with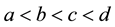 
where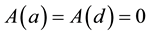 
and 
for all
. 
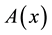for all
![]()
is known as left reference function and ![]()
for ![]()
is known as the right reference function. The left reference function is non-decreasing and the right reference function is non-increasing [12] .
The support of a fuzzy set ![]()
within a universal set ![]()
is the crisp set that contains all the elements of ![]()
that have non-zero membership grades in ![]()
and is denoted by![]()
. Thus
![]()
The core of a fuzzy set ![]()
within a universal set ![]()
is the crisp set that contains all the elements of ![]()
having membership grades 1 in![]()
.
Set Superimposition
When we overwrite, the overwritten portion looks darker for obvious reason. The set operation union does not explain this phenomenon. After all
![]()
and in ![]()
the elements are represented once only.
In [13] an operation called superimposition denoted by ![]()
was proposed. If ![]()
is superimposed over ![]()
or ![]()
is superimposed over![]()
, we have
![]()
(1)
where ![]()
are the elements of ![]()
represented twice, and ![]()
represents union of disjoint sets.
To explain this, an example has been taken.
If ![]()
and ![]()
are two real intervals such that![]()
, we would get a superimposed portion. It can be seen from (1)
![]()
(2)
where ![]()
.
(2) explains why if two line segments are superimposed, the common portion looks doubly dark [5] . The identity (2) is called fundamental identity of superimposition of intervals.
Let now, ![]()
and ![]()
be two fuzzy sets with constant membership value ![]()
everywhere (i.e. equi-fuzzy intervals with membership value![]()
). If ![]()
then applying (2) on the two equi- fuzzy intervals we can write
![]()
(3)
To explain this we take the fuzzy intervals ![]()
and ![]()
with constant membership value ![]()
given in Figure 1 and Figure 2. Here![]()
.
If we apply superimposition on the intervals then the superimposed interval will be consisting of![]()
, ![]()
and![]()
. Here the membership of ![]()
is (1) due to double representation and it is shown in Figure 3.
![]()
Figure 1. Equi-fuzzy Interval [1, 5](1/2).
![]()
Figure 2. Equi-fuzzy interval [3, 7](1/2).
Let![]()
, ![]()
, be ![]()
real intervals such that![]()
. Generalizing (3) we get
![]()
(4)
In (4), the sequence ![]()
is formed by sorting the sequence ![]()
in ascending order of magnitude for ![]()
and similarly ![]()
is formed by sorting the sequence ![]()
in ascending order.
Although the set superimposition is operated on the closed intervals, it can be extended to operate on the open and the half-open intervals in the trivial way.
Lemma 1. The Glivenko-Cantelli Lemma of Order Statistics
Let ![]()
and ![]()
be two random vectors, and ![]()
and
![]()
be two particular realizations of ![]()
and ![]()
respectively. Assume that the sub-![]()
fields induced by![]()
, ![]()
are identical and independent. Similarly assume that the sub-σ fields induced by
![]()
, ![]()
are also identical and independent. Let ![]()
be the values of![]()
, and ![]()
be the values of ![]()
arranged in ascending order.
For ![]()
and ![]()
if the empirical probability distribution functions ![]()
and ![]()
are defined as in (5) and (6) respectively. Then, the Glivenko-Cantelli Lemma of order statistics states that the mathematical expectation of the empirical probability distributions would be given by the respective theoretical probability distributions.
![]()
(5)
![]()
(6)
Now, let ![]()
is random in the interval ![]()
and ![]()
is random in the interval ![]()
so that ![]()
and ![]()
are the probability distribution functions followed by ![]()
and ![]()
respectively. Then in this case Glivenko-Cantelli Lemma gives
![]()
(7)
It can be observed that in Equation (4) the membership values of![]()
, ![]()
look like empirical probability distribution function ![]()
and the membership values of![]()
, ![]()
look like the values of empirical complementary probability distribution function or empirical survival function![]()
.
Therefore, if ![]()
is the membership function of an L-R fuzzy number![]()
. We get from (ix)
![]()
(8)
Thus it can be seen that ![]()
can indeed be the Dubois-Prade left reference function and ![]()
can
be the Dubois-Prade right reference function [13] . Baruah [14] has shown that if a possibility distribution is viewed in this way, two probability laws can, indeed, give rise to a possibility law.
4. Algorithm Proposed
If the time-stamps stored in the transactions of temporal data are the time hierarchy of the type hour_day_ month_year, then we do not consider month_year in time hierarchy and only consider day. We extract frequent item sets using method discussed in [3] . Each frequent item set will have a sequence of time intervals of the type (day 1, day 2) associated with it where it is frequent. Using the sequence of time intervals we can find the set of superimposed intervals (Definition of superimposed intervals is given in Section 3) and each superimposed intervals will be a fuzzy intervals. The method is as follows: for a frequent item set the set of superimposed intervals is initially empty, algorithm visits each intervals associated with the frequent item set sequentially, if an interval is intersecting with the core of any existing superimposed intervals (Definition of core is given in Section 3) in the set it will be superimposed on it and membership values will be adjusted else a new superimposed intervals will be started with the this interval. This process will be continued till the end of the sequence of time intervals. The process will be repeated for all the frequent item sets. Finally each frequent item sets will have one or more superimposed time intervals. As the superimposed time intervals are used to generate fuzzy intervals, each frequent item set will be associated with one or more fuzzy time intervals where it is frequent. Each superimposed intervals is represented in a compact manner discussed in Section 3.
For representing each superimposed interval of the form
![]()
![]()
we keep two arrays of real numbers, one for storing the values ![]()
and the other for storing the values ![]()
each of which is a sorted array. Now if a new interval ![]()
is to be superimposed
on this interval we add ![]()
to the first array by finding its position (using binary search) in the first array so that it remains sorted. Similarly ![]()
is added to the second array.
Data structure used for representing a superimposed interval is
struct superinterval
{ int arsize, count;
short *l, *r;
}
Here arsize represents the maximum size of the array used, count represents the number of intervals superimposed, and ![]()
and ![]()
are two pointer pointing to the two associated arrays.
Algorithm 4.1
for each locally frequent item sets do
{L ¬ sequence of time intervals associated with s
Ls ¬ set of superimposed intervals initially set to null
lt = L. get ();
// lt is now pointing to the first interval in L
Ls. append (lt);
while ((lt = L.get ()) != null)
{flag = 0;
while ((lst = Ls.get ()) ! = null)
if (compsuperimp (lt, lst))
flag = 1;
if (flag == 0) Ls. append (lt);
}
}
Compsuperimp (lt, lst)
{ if (÷ intersect (lst, lt)÷ != null)
{ superimp(lt, lst);
return 1;
}
return 0;
}
The function compsuperimp (lt, lst) first computes the intersection of lt with the core of lst. If the intersection non-empty it superimposes lt by calling the function superimp (lt, lst) which actually carries on the superimposition process by updating the two lists associated as described earlier. The function returns 1 if lt has been superimposed on the lst otherwise returns 0. get and append are functions operating on lists to get a pointer to the next element in a list and to append an element into a list.
5. Results Obtained
For experimentation purpose we have used retail market basket dataset from an anonymous Belgian retail store. The dataset contains 88,162 transactions and 17,000 items. This dataset does not have attribute, so time was incorporated on it. The domain of the time attribute was set to the calendar dates from 1-1-2001 to 30-2-2003. For the said purpose, a program was written using C++ which takes as input a starting date and two values for the minimum and maximum number of transactions per day. A number between these two limits are selected at random and that many consecutive transactions are marked with the same date so that many transactions have taken place on that day. This process starts from the first transaction to the end by marking the transactions with consecutive dates (assuming that the market remains open on all week days). This means that the transactions in the dataset are happened in between the specified dates. A partial view of the generated monthly fuzzy frequent item sets from retail dataset is shown in Table 1.
6. Conclusions and Lines for Future Work
An algorithm for finding monthly fuzzy patterns is discussed in this paper. The method takes input as a list of time intervals associated with a frequent item set. The frequent item set is generated using a method similar to the method discussed [4] . However, in our work we do not consider the month_year in the time hierarchy and only consider day. So each frequent item set will be associated with a sequence of time intervals of the form (day 1, day 2) where it is frequent. The algorithm visits each interval in the sequence one by one and stores the intervals in the superimposed form. This way each frequent item set is associated with one or more superimposed time intervals. Each superimposed interval will generate a fuzzy time interval. In this way each frequent item set is associated with one or more fuzzy time intervals. The nicety about the method is that the algorithm is less user-dependent, i.e. fuzzy time intervals are extracted by algorithm automatically.
Future work may be possible in the following ways.
Daily patterns can be extracted.
![]()
Table 1. Monthly fuzzy frequent item sets for different set of transactions.
Clustering of patterns can be done based on their fuzzy time interval associated with yearly patterns using some statistical measure.