A Study on the Seismic Isolation Systems of Bridges with Lead Rubber Bearings ()
Keywords:
1. Introduction
Seismic isolation systems are the separating of structures (such as bridge, building, railway, road, airport, harbor, dam, and tunnel etc.) from ground motions generated by earthquakes which could induce damage to the structures. Among various seismic isolation systems, lead-rubber bearing (LRB) which has innovative mechanism can lead to increased effective stiffness and is accommodating force in reinforced concrete (RC) structures. LRB is a novel apparatus based on the combination of laminated layers rubber bearing using lead plugs (Constantinou, et al. (2006) [1] ). In this research, a bridge was selected to demonstrate the application of analysis and bearing design procedures for seismic isolation system. The bridge was used as an example of bridge design without an isolation system in the Federal Highway Administration (FHWA) Seismic Design Course, Design Example No. 4, prepared by Berger/Abam Engineers (1996) [2] . The bridge is a continuous, three-span, cast-in-place concrete box girder structure with a 30-degree skew. The two intermediate bents consist of two round columns with a crossbeam on top. The geometry of the bridge, section properties and foundation properties are assumed to be the same in the original bridge in the FHWA example (2000) [3] . It is presumed that the original bridge design is sufficient to sustain the loads and displacement demands when seismically isolated as described herein. Only minor changes in the bridge geometry were implemented in order to facilitate seismic isolation.
2. Description of Bridge
Figures 1-3 show, respectively, the plan and elevation, the abutment sections and a section at an intermediate bent. In Figure 3, the bent is shown at the skew angle of 30 degrees, whereas for the box girder the section is perpendicular to the longitudinal axis. The actual distance between the column centerlines is 7.92 m (Figure 1).
![]()
Figure 1. Bridge plan view and elevation.
![]()
Figure 3. Cross section at intermediate bent.
The bridge is isolated with two multi-directional seismic isolators at each abutment and pier location for a total of eight multi-directional seismic isolators with lead rubber bearings. The isolators are directly located above the circular columns. The plan views of the isolated bridge are shown in Figure 4.
The bridge is isolated with two isolators at each abutment and pier location for a total of eight isolators. The isolators are directly located above the circular columns. The use of two isolators versus a larger number is intentional for the following reasons:
・ With elastomeric bearings it is possible to achieve a larger period of isolation (more mass per bearing).
・ The distribution of load on each isolator is accurately calculated. The use of more than two isolators per location would have resulted in uncertainty in the calculation of the axial load in vertically stiff bearings.
・ Reduction in construction cost.
For better distribution of load to the bearings, diaphragms are included in the box girder at the abutment and pier locations above the isolators. An additional 596 kN weight at each diaphragm location is introduced by the addition of these diagrams. The bridge is considered to have three traffic lanes. Loadings were determined based on AASHTO LRFD Specifications (2001) [4] with live load consisting of truck, lane and tandem and wind load being representative of typical sites in the Western United States.
Figure 5 shows a model for the analysis of the bridge. The model may be used in static and multimode analysis.
The cross sectional properties of the bridge and weights are presented in Table 1. The modulus of elasticity of concrete is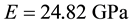 . Foundation spring constants are presented in Table 2.
. Foundation spring constants are presented in Table 2.
2.1. Analysis of Bridge for Dead, Live, Brake and Wind Loadings
The weight of the seismically isolated bridge superstructure is 22,650 kN. The difference is due to the presence now of diaphragms at the abutment and pier locations in order to transfer loads to the bearings. Kim (2007) [5] presents calculations for the bearing loads and rotations due to dead, live, braking and wind forces. Table 3 presents a summary of bearing loads and rotations. On the basis of the results in Table 3, the bearings do not experience uplift or tension for any combination of dead and live loadings.
![]()
Figure 4. Plan view of bridge isolated with lead-rubber bearings.
![]()
Figure 5. Model of bridge for single- and multimode analysis.
![]() *: Coordinates X, Y and Z refer to the local member coordinate system; **: Cracked section properties (0.7 Ig); ***: Add 596 kN concentrated weight at each bent and abutment location; ****: Total weight of footing divided by length of 0.53 m.
*: Coordinates X, Y and Z refer to the local member coordinate system; **: Cracked section properties (0.7 Ig); ***: Add 596 kN concentrated weight at each bent and abutment location; ****: Total weight of footing divided by length of 0.53 m.
Table 1. Cross sectional properties and weights in bridge model.
![]()
Table 2. Foundation spring constants in bridge model.
![]() V: Vertical reaction; T: Transverse reaction; +: Compressive force; −: Tensile force.
V: Vertical reaction; T: Transverse reaction; +: Compressive force; −: Tensile force.
Table 3. Bearing loads and rotations due to dead, live, brake and wind loads.
2.2. Seismic Loading
Seismic loading is defined per Caltrans Seismic Design Criteria (2004) [6] to be the 5%-damped response spectrum of Magnitude 7.25, 0.7 g acceleration and soil profile C. The horizontal response spectra for acceleration and displacement are shown in Figure 6. This earthquake is considered to be the Maximum Earthquake. Calculations are performed only for this earthquake level and isolator safety checks are performed on the basis of the calculated response at this level. The vertical earthquake is assumed to be described by the spectra of Figure 6 after multiplication by factor 0.70.
![]()
Figure 6. Horizontal 5%-damped response spectra for earthquake of magnitude 7.25 and soil profile type C (Adapted from Clatran Seismic Design Criteria (2004) [6] ).
3. Design Analysis of Lead-Rubber Isolation System
This case study is developed as an alternative to the combined lead-rubber and elastomeric bearing isolation system (Constatinou, et al., 2007 [7] ). The combined system may not be desirable because two different isolator types are used in an application with only eight bearings. An all lead-rubber bearing system is simpler and requires less testing.
3.1. Single Mode Analysis
Criteria for applicability of single mode analysis are presented in Table 4. Kim (2007) [5] presents the calculations for the analysis and safety check of the isolation system. The all pier abutment and pier bearings are lead-rubber bearings with 200 mm diameter lead core. All bearings are of identical construction and of identical materials. Drawing of the bearings is shown in Figure 7. The bearings need not be installed pre-deformed in order to accommodate displacements due to post-tensioning and shrinkage. The bearings are safe for a service displacement of 75 mm (includes shrinkage and post-tensioning effects) and 455 mm seismic displacement.
Table 5 presents a summary of the calculated displacement and force demands, the effective properties of the isolated structure and the effective properties of each type of bearing. These properties are useful in response spectrum, multi-mode analysis. The effective stiffness was calculated using
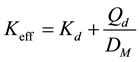 (1)
(1)
where (a) for abutment bearing, 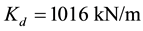 and
and 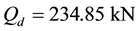 for lower bound and
for lower bound and
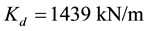 and
and ![]() for upper bound, and (b) for each pier bearing,
for upper bound, and (b) for each pier bearing, ![]() and
and ![]() for lower bound and
for lower bound and ![]() and
and ![]() for upper bound.
for upper bound.
![]()
Table 4. Applicability criteria for methods of analysis.
![]()
Table 5. Applicability criteria for methods of analysis.
1Based on one-directional excitation in longitudinal bridge direction; 2Based on three-directional excitation using 100% - 30% - 30% rule, and multiplying by Factor 1.1; 3Value is for 100% vertical + 30% transverse + 30% longitudinal combination (maximum axial load); 4Value is for 100% transverse + 30% vertical + 30% longitudinal combination (worst case for lead-rubber bearing safety check-combined with maximum bearing displacement).
![]()
Figure 7. Principle structure and size of LRB for bridge example.
3.2. Multimode Response Spectrum Analysis
Figure 8 shows the bridge model used for response spectrum analysis. For this analysis, each isolator is modeled as a vertical 3-dimentional beam element-rigidly connected at its two ends-of length![]() , area
, area![]() , moment of inertia about both bending axes
, moment of inertia about both bending axes ![]() and torsional constant
and torsional constant![]() . The element length is the height of the bearing,
. The element length is the height of the bearing, ![]() (average height of bearings) and the area is calculated as described below in order to represent the vertical bearing stiffness. Note that the element is intentionally used with rigid connections at its two ends so that
(average height of bearings) and the area is calculated as described below in order to represent the vertical bearing stiffness. Note that the element is intentionally used with rigid connections at its two ends so that ![]() effects are properly distributed to the top and bottom parts of the bearing. The vertical bearing stiffness was calculated using the theory presented in Section 9 of the report (Constantinou, et al., (2007) [7] ). Particularly, the vertical stiffness in the laterally un-deformed configuration is given by
effects are properly distributed to the top and bottom parts of the bearing. The vertical bearing stiffness was calculated using the theory presented in Section 9 of the report (Constantinou, et al., (2007) [7] ). Particularly, the vertical stiffness in the laterally un-deformed configuration is given by
![]() (2)
(2)
In Equation (2), ![]() is total rubber thickness,
is total rubber thickness, ![]() is the bonded rubber area (however adjusted for the effects of rubber cover by adding the rubber thickness to the rubber bonded diameter),
is the bonded rubber area (however adjusted for the effects of rubber cover by adding the rubber thickness to the rubber bonded diameter), ![]() is the bulk modulus of rub- ber (assumed to be 2000 MPa). Moreover,
is the bulk modulus of rub- ber (assumed to be 2000 MPa). Moreover, ![]() is the compression modulus given by
is the compression modulus given by
![]() (3)
(3)
where ![]() is the shear modulus of rubber,
is the shear modulus of rubber, ![]() is the shape factor and
is the shape factor and ![]() is given by Equation (4) below with
is given by Equation (4) below with ![]() and
and ![]() being the outside and inside bonded diameters of the bearing. Note that for the calculation of the vertical stiffness of the lead-rubber bearing we consider that the lead core does not exist and treat the bearing as one without a hole for which parameter
being the outside and inside bonded diameters of the bearing. Note that for the calculation of the vertical stiffness of the lead-rubber bearing we consider that the lead core does not exist and treat the bearing as one without a hole for which parameter![]() . Also, we used the nominal value of shear modulus
. Also, we used the nominal value of shear modulus ![]() under static conditions in order to obtain a minimum value of vertical stiffness that can also be used in the bearing performance specifications.
under static conditions in order to obtain a minimum value of vertical stiffness that can also be used in the bearing performance specifications.
![]() (4)
(4)
Torsional constant is set ![]() or a number near zero since the bearing has insignificant torsional resistance. Moreover, shear deformations in the element are de-activated. The moment of inertia of each element is calculated by use of the following equation
or a number near zero since the bearing has insignificant torsional resistance. Moreover, shear deformations in the element are de-activated. The moment of inertia of each element is calculated by use of the following equation
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 8. First three modes of vibration of isolated bridge with lead-rubber bearing system in lower bound analysis. (a) First mode: T1 = 2.67 sec; (b) Second mode: T2 = 2.61 sec; (c) Third mode: T3 = 2.21 sec.
![]() (5)
(5)
Response spectrum analysis was performed using the response spectrum of Figure 8 for 0.7 g which is 5%-damped spectrum after division by parameter B for periods larger or equal to 0.8 TM, where TM is the effective period and B is the parameter that relates the 5%-damped spectrum to the spectrum at the effective damping. Quantities TM, B and the effective damping are presented in Table 5. It should be noted that these quantities are given in Table 5 for the upper and lower bound cases, both of which are analyzed. Values of 0.8 TM are 1.3 sec for upper bound analysis and 2.0 sec for lower bound analysis. Values of parameters used in response spectrum analysis of lead-rubber bearing isolation system are presented in Table 6. Besides, values of spectral acceleration used in the analysis are presented in Table 7.
Eigenvalue and response spectrum analysis were performed in program SAP2000 [8] . Figure 8 presents the mode shapes of the first three modes of vibration of the isolated bridge in the lower bound analysis. They are two modes dominated by translational displacements in two orthogonal directions, and a third torsional mode of vibration. The results are qualitatively the same as those for the combined lead-rubber and elastomeric bearing system with the first mode characterized by deformation of both the isolators and the piers along the weak direction of the pier. The period matches nearly exactly the period that is calculated in simplified analysis accounting for the effects of substructure flexibility (T = 2.67 sec). The second mode is deformation along the strong axis of the pier and accordingly it consists primarily of isolator deformation. This period matches nearly the period calculated neglecting the effect of substructure flexibility (T = 2.58 sec).
Analysis was performed by separately applying the earthquake excitation in the longitudinal, transverse and vertical bridge directions. The vertical response spectrum was taken as a 70% portion of the horizontal 5%- damped spectrum without any modification for increased damping.
The results of these analyses are presented in Table 8 in terms of the bearing displacements; isolation shear force and bearing axial forces (only part due to earthquake). Table 8 presents a comparison of key response quantities obtained by the single and multimode-response spectrum methods of analysis. In each type of analysis, quantity DTM was calculated as the vectorial sum of bearing displacements due to longitudinal and transverse earthquake components combined using the 100% - 30% rule and then multiplying by Factor 1.1. The results demonstrate very good agreement in the calculated bearing displacement demands and isolation shear forces between the two methods of analysis.
Axial bearing forces are underestimated by the single mode analysis method due, primarily, to neglect of the skew in the calculations. Consideration of the skew angle is not difficult but the underestimation in the calculation of loads to have any significance in the safety of the bearings. Calculations show that the bearings have capacity to sustain the calculated loads in the maximum earthquake.
![]()
Table 6. Values of parameters h, A, I and E used in response spectrum analysis of lead-rubber bearing isolation system.
![]() *Vertical excitation spectrum is 0.7 times the 5%-damped horizontal spectrum.
*Vertical excitation spectrum is 0.7 times the 5%-damped horizontal spectrum.
Table 7. Spectral acceleration values used in response spectrum analysis of isolated bridge with lead-rubber bearing system.
![]() Note: (P) denotes the pier bearings and (A) denotes the abutment bearings.
Note: (P) denotes the pier bearings and (A) denotes the abutment bearings.
Table 8. Key response quantities obtained by multimode analysis isolated bridge with lead-rubber bearing system.
4. Conclusions
The examples presented in this paper demonstrate that single-mode and multi-mode analysis methods, when properly implemented, provide results in close agreement. On the basis of the results obtained in this study, the single mode method of analysis is sufficiently accurate and conservative to be used in analysis and design.
Examples of specifications which are consistent with the assumptions made in the analysis have been presented in this study. Table 9 presents a summary of key response quantities for the two example designs of this paper as obtained by the single mode method of analysis. These quantities are the total maximum dis-
![]() *Constantinou, et al. (2007).
*Constantinou, et al. (2007).
Table 9. Comparison of key response quantities for two examples as obtained by single mode method of analysis (W = 22,650 kN).
1) Total displacement ![]() on design for all Lead-Rubber bearings case is reduced comparing with combined lead-rubber and elastomeric bearing system
on design for all Lead-Rubber bearings case is reduced comparing with combined lead-rubber and elastomeric bearing system![]() . As a result, this represents substantial reduction in cost because of reduction of expansion joint.
. As a result, this represents substantial reduction in cost because of reduction of expansion joint.
2) In lower bound analysis, the benefit of all LRB versus Elastomeric bearing/LRB is almost 2% reduction in shear force at pier. When ![]() ratio is reduced, the force at pier is reduced by increasing stiffness.
ratio is reduced, the force at pier is reduced by increasing stiffness.
3) Furthermore, while previous design requires tests for two types of bearing, another benefit is that construc- tion and testing is needed to only one type of bearing.
Acknowledgements
The authors would like to gratefully acknowledge Professor Michael C. Constantinou for his advice to this study. This research was supported by research fund, Kumoh National Institute of Technology.
NOTES
*Corresponding author.