The Mathematics of Harmony. Proclus’ Hypothesis and New View on Euclid’s Elements and History of Mathematics Starting since Euclid ()
1. Preface
Algebra and Geometry have one and the same fate. The very slow successes followed after the fast successes at the beginning. Mathematicians left science in a state very far from perfect. It happened, probably, because Mathematicians drew all their attention on the Advanced Parts of Analysis, by neglecting the origin of Mathematics and not wishing to dig in the field, which they already went through and had left behind.
Nikolay Lobachevsky
2. Introduction
Euclid’s Elements is the greatest mathematical work of the ancient Greek era. This scientific work was created by Euclid (Figure 1) in the 3d century BC and contained the foundations of ancient mathematics: elementary geometry, number theory, algebra, theory of proportions and relations, methods of determining areas and volumes, and others. In this work Euclid presented the result of the Greek mathematics development during 3 centuries and created a powerful foundation for further development of mathematics.
Euclid’s Elements is an inexhaustible source of new mathematical findings. Lobachevsky’s geometry, which arose as a result of the deep mathematical analysis of Euclid’s V-th postulate (the “postulate about parallel lines”) is a brilliant example of this.
This article reveals another secret of Euclid: for what purpose Euclid introduced the “problem of the division of a line segment in extreme and mean ratio”? In modern science, this division is called the “golden section”. Euclid introduced the “golden section” in the Book II (Proposition II.11). Euclid then considered the “golden section” in the Book VI. The most often the Propositions, concerning to the “golden section,” are found in the Book XIII, which is devoted to the geometric theory of regular polyhedra (“Platonic solids”).
Modern historians of mathematics are not very often discuss the role of the “golden section” in Euclid’s Elements and prefer to keep silent about this and, unfortunately, they do not answer the question: what was the purpose of Euclid to introduce the “golden section” in his famous mathematical work. The purpose of this article is to uncover one of the greatest mysteries of Euclid’s Elements, associated with the “golden section”.
Greek philosopher and mathematician Proclus Diadochus (410-485) was one of the first brilliant commentators of Euclid’s Elements. He was first thinker, who tried to uncover this secret. He put forward the most unusual hypothesis in the history of mathematics. The essence of Proclus’ hypothesis consists in the fact that the main purpose of Euclid when writing the Elements was to build a complete geometric theory of Platonic solids. This theory has been placed in the Book XIII, that is, in the concluding Book of the Elements. Because the most important material of scientific book is usually placed in the final part of the book, the fact that the theory of Platonic solids was placed by Euclid in the Book XIII, that is, the concluding book of the Elements, is an indirect confirmation of Proclus’ hypothesis.
Because the Platonic solids were associated in ancient Greek science with the “Universe Harmony”, it follows from this fact that Euclid’s Elements were written under the direct influence of the “harmonic ideas” of Pythagoras and Plato. This is the main secret of Euclid’s Elements. From these reasonings, it follows another interesting conclusion: Euclid’s Elements are historically the first attempt to create the “Mathematical Principles of the Universe Harmony”. And since mathematics as a science was formed under the powerful influence of Euclid’s Elements, we must admit that the main goal of mathematics is to discover the mathematical
laws of the Universe Harmony. From these considerations it follows another important conclusion: the role of the “golden section” and the Platonic solids should be increased in mathematics and especially in mathematics education. Modern mathematicians have not yet grasped these important conclusions.
According to the author, the “golden section” was introduced by Euclid in his Elements not accidental. Euclid was in need of the “golden section” to construct the geometric theory of “dodecahedron”, one of the main Platonic Solids. That’s why the Book XIII, the concluding Book of the Elements, contains the largest number of Proposals relating to the “golden section”.
In modern science, interest in the “golden section” and the Platonic solids increased significantly. Two scientific discoveries of modern science (fullerenes and quasi-crystals), based on the “golden section” and Platonic solids, has been awarded the Nobel Prize in chemistry. That is, the modern theoretical natural sciences make an extensive use of the well-known geometric discoveries of the ancient Greeks―the “golden section” and Platonic solids.
The author’s book The Mathematics of Harmony. From Euclid to Contemporary Mathematics (World Scientific, 2009) http://www.worldscientific.com/worldscibooks/10.1142/6635, which in its origins dates back to Euclid’s Elements, is a reflection of one of the most important trends in the development of modern science― the revival of “harmonic ideas” Pythagoras, Plato and Euclid. Proclus hypothesis plays a central role in this revival.
3. The Idea of the Universe Harmony in the Ancient Greek Science
3.1. What Is the Harmony?
As pointed out by the Russian philosopher VP Shestakov in the book “Harmony as an Aesthetic Category” [1] “the history of aesthetic doctrines puts forward a variety of types of understanding harmony. The very concept of “harmony” is used very widely and has many meanings. It signified the natural construction of nature and cosmos, the beauty of the physical and moral world of a man, the principles of the construction of art works, and the laws of aesthetic perception.”
Shestakov identifies three basic understandings of harmony, prevailing in the development of science and aesthetics:
1). Mathematical understanding of harmony or mathematical harmony. In this sense, harmony is understood as equality or proportionality of parts with each other and part with the whole. In the Great Soviet Encyclopaedia, we find the following definition of harmony, which expresses the mathematical understanding of harmony:
“Harmony is a proportionality of parts with the whole, the confluence of the various components of the object into a single organic whole. In the harmony, the internal ordering and the measure of being get the external manifestation.”
2). Aesthetic harmony. In contrast to the mathematical understanding of the harmony, the aesthetic understanding is not only quantitative but also qualitative, and expresses the inner nature of things. The aesthetic harmony associated with aesthetic experiences, with an aesthetic evaluation. Most clearly this type of harmony is manifested in the perception of the nature beauty.
3). Artistic harmony. This type of harmony is associated with art. The artistic harmony is the actualization of the principle of harmony in the material of art itself.
Most importantly, it follows from the arguments, given in [1] , that the “harmony” is a universal concept that is relevant not only to mathematics and science but also to arts.
3.2. Numerical Harmony of the Pythagoreans
Pythagoras (Figure 2) and Heraclitus (Figure 3) are Greek thinkers whose names are usually attributed to the beginning of the philosophical doctrine of the harmony. According to many authors, the key idea of the harmony as a commensurate unity of opposites belongs to Pythagoras. Pythagoreans first proposed the idea of the harmonic organization of the world, including not only man and nature, but also the entire cosmos. According to the Pythagoreans, “the harmony represents the internal relationship of things, without which the cosmos could not exist.” Finally, according to Pythagoras, the harmony has a numeric expression, that is, it is integrally linked to the concept of number.
Pythagoreans created the doctrine about constructive essence of a number. Aristotle in his “Metaphysics”
![]()
Figure 2. Pythagoras (approx. 570-c. 500 BC).
notes this particular feature of the Pythagorean doctrine as follows:
“The so-called Pythagoreans, by exploring the mathematical sciences, for the first time advanced them forward and, by taking them as the basis, began to consider them the principle of all things... Since all the rest is explicitly likened to the numbers by the essence, therefore the numbers occupied the first place in the whole nature, therefore the elements of numbers, named the elements of all things and the whole universe, were recognized by harmony and number.”
3.3. Heraclitus’ Contribution to the Development of the Harmony Doctrine
From antiquity up to the present day, the name of Heraclitus remains one of the most popular in the history of philosophy.
Heraclitus believed that everything is constantly changing. Heraclitus connects an assertion about the general variability with the idea of the inner division of things and processes on opposite parts, with their constant interaction. Heraclitus believed that everything in life arises from opposites and is cognized through them. The idea of perpetual motion was embodied by Heraclitus in the image of ever-flowing river. The postulate about the general changeability of the world, as one of the cornerstones of the entire dialectics, was formulated by Heraclitus in the famous formula: “One can not enter twice in the same river.”
The moment of evaluation is characteristic for Heraclitus’ aesthetics. Especially clearly such evaluation expressed in the doctrine about the two kinds of harmony: the “hidden” and “explicit”. Heraclitus gives preference for the “hidden” harmony. It is widely known the following saying of Heraclitus: “The hidden harmony is stronger explicit”.
Cosmos, as the supreme and perfect beauty, is an example of the “hidden” harmony. Only at first glance the world seems chaos. In fact, “the marvelous harmony” is hiding for the game of elements and randomness.
3.4. Pythagorean Musical Harmony and Music of the Spheres
Pythagoreans made remarkable discoveries in music. Pythagoras discovered that the most pleasant hearing harmonies―consonances―are obtained only in the case where the length of the strings, which produce these sounds, relate as the first natural numbers 1, 2, 3, 4, 5, 6, that is, 1:1, 1:2 (an unison and an octave), 2:3, 3:cv 4 (a fifth and a fourth), 4:5, 5:6 (a third), etc. This discovery shocked Pythagoras. This discovery first pointed out on the existence of numerical regularities in nature and was the starting point in the development of Pythagorean philosophy, based on the thesis: “Everything is a number”. Therefore, the day when Pythagoras discovered the law of consonances, the German physicist Arnold Sommerfeld called the birthday of theoretical physics.
The discovery of mathematical regularities in musical consonances became the first “experimental” proof of Pythagoras’ doctrine of numbers. From that moment, the music and the associated with it doctrine of the harmony begin to occupy a central place in the Pythagorean system of knowledge. The Pythagorean idea of musical relations soon acquired the “cosmic scale” and grew into the idea of the universal or global, harmony.
Pythagoreans began to claim that the Universe is arranged on the basis of simple numerical relations and that the moving planets produce “music of the heavenly spheres”, but the traditional music is merely a reflection of the prevailing everywhere “universal harmony”. Thus, music and astronomy were reduced by the Pythagoreans to the analysis of numerical laws, that is, to the arithmetic and geometry. Thus, all four disciplines are mathematical and called by one word―“Mathematics”.
3.5. Plato’s Cosmology
The Greeks made the first attempt to “mathematize harmony”, that is, to express the harmony in numerical and geometric form. According to Edward Soroko [2] , “the ancient Greeks associated the idea about the “universal harmony” of the Universe with its implementation in the Platonic solids.” In other words, the regular polyhedra, called Platonic solids after the prominent Greek philosopher Plato (Figure 4), were considered as the indicators of the geometric harmony of the Universe.
There are only five Platonic solids (this was proved in Euclid’s Elements): tetrahedron, hexahedron or cube, octahedron, dodecahedron, and icosahedron (Figure 5).
According to Plato, the first four of the five regular solids (tetrahedron, icosahedron, cube and octahedron) embodied in themselves the main four “elements” (fire, water, land, air). Tetrahedron symbolized the fire, because its apex directed upwards; icosahedron symbolized the water, because it is the most “streamlined” polyhedron; cube symbolized the land, because it is the most “sustainable” polyhedron; octahedron symbolized the air as the most “air” polyhedron. The fifth polyhedron, the dodecahedron, embodied in itself “all things”, “Universal Mind”, was a symbol of the ether and was considered the main geometrical figure of the Universe.
Pythagorean doctrine about the numerical harmony of the Universe had a huge creative force and had a great influence on the development of all subsequent doctrines on the nature and essence of harmony, in particular, it was the basis of Plato’s cosmology. In his works, Plato develops the Pythagorean doctrine, especially emphasizing the cosmic significance of harmony. He is firmly convinced that the harmony of the world can be expressed in numerical proportions. The influence of the Pythagoreans is especially evident in Plato’s “Timaeus”, where after the Pythagoras, Plato developed the theory of proportions and analyzed the role of regular polyhedra (“Platonic solids”), from which, in his opinion, God created the world.
The main conclusion, which follows from Pythagoras and Plato’s doctrines, consists in the fact that the
![]()
Figure 4. Plato (428/427 or 424/423 BC-348/347 BC).
![]()
Figure 5. Platonic solids: tetrahedron, octahedron, cube, dodecahedron, icosahedrons.
harmony is objective phenomenon, it exists independently of our consciousness and is expressed in the harmonious organization of everything, starting with the Cosmos and ending by microcosm. But if the harmony is objective, it should be the subject of mathematical research.
This idea underlies Alexey Stakhov’s (2009) book “The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science” [3] . The main purpose of this book is to develop and generalize the mathematical concepts that are relevant to the harmony and emerged in science for several millennia. The next goal of the book is to show perspectives of the applications of the “mathematics of harmony” for the solution of the vital problems of modern science.
3.6. About the Term of “the Mathematics of Harmony”
For the first time, the term of “the Mathematics of Harmony” was used in the article “Harmony of spheres”, published in “The Oxford dictionary of philosophy” [4] :
Harmony of spheres. A doctrine often traced to Pythagoras and fusing together mathematics, music, and astronomy. In essence the heavenly bodies being large objects in motion, must produce music. The perfection of the celestial world requires that this music be harmonious, it is hidden from our ears only because it is always present. The mathematics of harmony was a central discovery of immense significance to the Pythagoreans.
Thus, the concept of the “Mathematics of Harmony” is associated here with the “harmony of the spheres”, which is also called the “harmony of the world” (Latin “harmonica mundi”) or world music (Latin “musical mundane”). The harmony of the spheres [4] is the ancient and medieval doctrine about the musical-mathemati- cal organization of Cosmos that goes back to the Pythagorean and Platonic philosophical tradition.
Another mention about the “Mathematics of Harmony”, as the ancient Greek great discovery, we find in the book by Vladimir Dimitrov, A new kind of social science. Study of self-organization of human dynamics [5] . Let us consider the quote from the book:
Harmony was a key concept of the Greeks, a conjunction of three strands of meaning. Its root meaning was aro, join, so harmonia was what joined. Another meaning was proportion, the balance of things that allowed an easy fit. The quality of joining and proportion then came to be seen in music and other arts.
The precondition for harmony for the Greeks was expressed in the phrase “nothing to much”. It also had a mysterious positive quality, which became the object of enquiry of their finest minds. Thinkers such as Pythagoras sought to capture the mystery of harmony as something both inexpressible yet also illuminated by mathematics. The mathematics of harmony explored by the ancient Greeks is still an inspiring model for contemporary scientists. Crucial to it is their discovery of its quantitative expression in astonishing diversity and com-
plexity of nature through the golden mean (golden ratio), Ф (phi):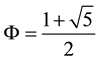 , which is approximately equal to
, which is approximately equal to
1.618. It is described by Euclid in book five of his Elements: “A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to greater, so is greater to the less”.
Thus, in the book [5] the concept of the “Mathematics of Harmony” is directly associated with the golden ratio―the most important ancient mathematical discovery in the field of harmony, which at that time was called the division of the line segment in extreme and mean ratio.
Finally, it is pertinent to mention that this term was used in Stakhov’s speech “The Golden Section and Modern Harmony Mathematics”, made at the 7th International Conference “Fibonacci Numbers and Their Applications” (Austria, Graz, 1996) [6] .
4. The Golden Section in Euclid’s “Elements”
4.1. Proposition II.11
In Euclid’s Elements we meet the task, which later had played a great role in the development of science. This task is called the “division of line segment in extreme and mean ratio”. In the Elements this task occurs in two forms. The first form is formulated in the Proposition 11 of the Book II.
Proposition II.11. Divide a given line segment  into two unequal parts
into two unequal parts  and
and  so that the area of the square, which is built on the larger segment
so that the area of the square, which is built on the larger segment 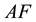 would be equal to the area of the rectangle, which is built on the segment
would be equal to the area of the rectangle, which is built on the segment 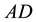 and the smaller segment
and the smaller segment .
.
Depict this problem geometrically (Figure 6).
Thus, according to the Proposition II.11, the area of the square AGHF should be equal to the area of the rectangle ABCD. If we denote the length of the larger segment AF through b (it is equal to the side of the square
![]()
Figure 6. A division of a line segment in extreme and mean ratio (the “golden ratio”).
AGHE), and the side of the smaller segment FD through a (it is equal to the vertical side of the rectangle ABCD), then the condition for the Proposition II.11 can be written as follows:
 . (1)
. (1)
In Euclid’s Elements, we meet another form of the “golden ratio”. This form follows from the first one, given by (1), if we make the following transformations. Dividing both parts of (1) at first by a, and then by b, we get the following proportion:
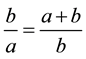 . (2)
. (2)
The proportion (2) has the following geometric interpretation (Figure 7). Divide the segment AB in the point C in such a relation when the larger part CB relates to the smaller part AC, as the segment AB to its larger part CB (Figure 7), that is,
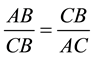 . (3)
. (3)
This is the definition of the “golden ratio”, used in modern science.
We denote the proportion (3) through x. Then, taking into consideration, that![]() , the proportion (3) can be written as follows:
, the proportion (3) can be written as follows:
![]() . (4)
. (4)
The following algebraic equation follows from (4):
![]() . (5)
. (5)
From the “physical meaning” of the proportion (5), it implies that we should use the positive root of the Equation (5). We denote this root through F:
![]() . (6)
. (6)
4.2. Mordukhai-Boltovsky’s Comments about the “Golden Section”
Euclid’s Elements are translated into many languages. The most authoritative Russian edition [7] -[9] is Euclid’s Elements in the translation and commentaries of the famous Russian historian of mathematics Prof. D.D. Mordukhai-Boltovsky (Figure 8).
Consider Mordukhai-Boltovsky’s comments about the “golden section”:
Now look at the place of the golden section in Euclid’s Elements. First of all, it should be noted that it arises in two forms, the difference between them is almost imperceptible to us, but was very significant in the eyes of the Greek mathematician of V-VI-th century BC. The first form, the prototype of which we have seen in Egypt, appears in the Book II of the Elements, namely in the Proposition 11 together with its preceding Proposals 5 and 6; here the golden ratio is defined as such ratio, for which the square, built on the larger segment, is equal to the rectangle, built on the whole line and the smaller segment. We can find the second form in the definition 3 of the Book VI, wherein the golden ratio is determined as the proportion of the whole line to the larger segment, and a larger segment to the smaller one and is called the division in extreme and mean ratio; in this form the golden section could be known only since Eudoxus’ time…
In the book XIII, the golden ratio is presented in the above two forms, namely in the first form in the Propositions 1 - 5, and in the second dorm in the Propositions 8 - 10…
![]()
Figure 8. D.D. Mordukhai-Boltovsky (1876-1952).
All this allows to think that Propositions 4, 7, 8 of the Book II and Propositions 1 - 5 of the book XIII represent the remains of one of the oldest in the history of Greek geometry document, which dated probably to the first half of the V century and emerged in the Pythagorean school, on the grounds of the material, which was brought from Egypt. Relative antiquity of this document can be ascertained from the fact that Propositions 4 and 7 of the Book II are used in it to prove a generalization of the Pythagorean theorem [the square of the side against acute and obtuse angle (Propositions 12 and 13 of the book II)], which, of course, was known to Hippocrates of Chios.”
Valentin Bunin in the book [10] also draws attention to “the Egyptian trace” in the origin of the “golden section”: “It is worth recalling that the original geometric meaning of the ‘golden section’ is very simple and has been associated with the annual redistribution of land area, flooded by Nile. In this case, the following problem was considered: to find the side of the rectangle, the area of which was equal to the area of the square, and the ratio of sides would provide ease of layout.”
4.3. The Origin of the Term of the “Golden Section”
Sometimes the introduction of the name of the “golden section” (“sectio aurea”) attributed to Leonardo da Vinci. However, it is believed that the great Leonardo was not the first. According to the statement of Edward Soroko [2] , the term goes back to Ptolemy’s book “On the harmony”. However, in the book [11] , devoted to the history of the “golden number”, there is stated that the German mathematician Martin Ohm first coined the term “golden section” (“goldene shnitt”) in 1835 in the book “Die reine Elementar-Mathematik”.
The designation of the “golden section” by the Greek letter F (the number of PHI) is not accidental. This letter is the first letter in the name of the famous Greek sculptor Phidias, who is widely used the “golden section” in his sculptural works.
4.4. Citations of Alexey Losev and Johannes Kepler
What is the main idea, which underlies the ancient Greek science? The vast number of researchers is inclined to the following answer: the idea of Harmony, associated with the “golden section”. As is known, in ancient Greek philosophy the Harmony is opposed to the Chaos and means organization of the Universe.
The outstanding Russian philosopher Alexey Losev (Figure 9), a researcher at the aesthetics of antiquity and the Renaissance, assesses the main achievements of the ancient Greeks in this field as follows:
“From Plato’s point of view, and in general from the point of view of the whole ancient cosmology, the world is presented as a certain proportional whole, which obeys to the law of harmonic division, the golden section… Their system of cosmic proportions in the literature often is presented sometimes as a curious result of unrestrained and wild imagination. In such explanations we can see the antiscientific helplessness of those, who this assert. However, the understanding of this historical and aesthetic phenomenon can only be in connection with a holistic understanding of history, that is, by using a dialectical materialist view on culture and by looking for answers in the peculiarities of ancient social life.”
In this statement Alexey Losev convincingly formulated the “golden” paradigm of ancient cosmology. It is based on the most important ideas of ancient science, which in modern science is sometimes interpreted as a “curious result of unrestrained and wild imagination”. First of all, this is the Pythagorean idea of the numerical harmony of the Universe and Plato’s cosmology, based on the Platonic solids. By turning to the geometric structure of the Universe and the arithmetic relations, expressing the harmony, the Pythagoreans anticipated the emergence of mathematical natural sciences, which began to develop rapidly in the 20th century. The idea of Pythagoras and Plato about the numerical harmony of the Universe proved to be immortal.
Thus, in the center of the created by the ancient Greeks mathematical doctrine of Nature was “the concept of harmony”, and mathematics itself of the ancient Greeks was the “Mathematics of Harmony”, which was directly related to the “golden section”, the most important mathematical discovery of ancient science in the field of harmony.
Here is another well-known statement, concerning the “golden section”. It belongs to the brilliant astronomer Johannes Kepler (Figure 10), the author of the three famous “Kepler’s laws”.
Kepler expressed his admiration for the “golden section” in the following words:
“Geometry has two great treasures: one is the Theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first, we may compare to a measure of gold; the second we may name a precious stone.”
Recall that the antique problem of the division of the line segment into extreme and mean ratio, which is referred to in this statement, is the “golden section”!
4.5. The Golden Section in the Dodecahedron and Icosahedron
The dodecahedron and the dual to it icosahedron occupy a special place among the Platonic solids (Figure 5). First of all, it is necessary to emphasize that the geometry of the dodecahedron and icosahedron is directly related to the “golden section”.
Indeed, the regular pentagon, based on the “golden section”, are the faces of the dodecahedron (Figure 5). If we look closely at the icosahedron (Figure 4), we can see that in each of its vertices the five triangles come together and their outer sides form the regular pentagon. Already these facts are enough to make sure that the golden ratio plays a decisive role in the construction of these two Platonic solids.
But there are the deeper mathematical confirmations of the fundamental role, played by the golden section in the icosahedron and dodecahedron. It is known that these Platonic solids have three characteristic spheres. The first (inner) sphere is inscribed in the Platonic solid and touches its faces. We denote the radius of the inner sphere through![]() . The second or middle sphere touches its ribs. We denote the radius of this sphere through
. The second or middle sphere touches its ribs. We denote the radius of this sphere through![]() .
.
Finally, the third (outer) sphere is described around the Platonic solid and passes through its vertices. We denote its radius through. In geometry, it is proved that the values of the radii of these spheres for the dodecahedron and icosahedron, which have the ribs of unit length, expressed in terms of the golden ratio (Table 1).
Note, that the ratio of the radii ![]() is the same for the icosahedron and dodecahedron. Thus, if
is the same for the icosahedron and dodecahedron. Thus, if
the dodecahedron and icosahedron have the same inscribed spheres, then their described spheres are equal. The proof of this mathematical result is given in Euclid’s Elements.
4.6. Ancient Greeks’ Mathematical Doctrine about Nature
According to the eminent American historian of mathematics Morris Kline [12] , the main ancient Greeks’ contribution, “which had a decisive influence on all subsequent culture, consists in the fact that they begun to study the laws of Nature.” The main conclusion to be drawn from Morris Kline’s book [12] is the fact that the ancient Greeks offered the innovative concept of the Cosmos, where everything was subordinated to mathematical laws. The question arises: when this concept was developed? The answer to this question is also found in the book [12] .
In the book [12] it is assumed that the innovative concept of the Cosmos has been developed by the ancient Greeks during VI-III c. BC.
But according to the prominent Russian mathematician A.N. Kolmogorov [13] , in the same period (VI-III c. BC.) in the ancient Greece “there arises mathematics as an independent science with a clear understanding of
![]()
Table 1. The Golden Ratio in the spheres of the dodecahedron and icosahedrons.
the uniqueness of its method and the need for systematic development of its basic concepts and proposals in a rather general way.”
But then the question arises: whether there is any relationship between the process of creating a mathematical doctrine about the Nature what is considered as the most important achievement of the ancient Greek science [12] , and the process of creation of mathematics, which was developed in the ancient Greece in the same period? Or those are different processes? It turns out that such a relationship existed definitely. Moreover, it can be argued that these processes actually coincided. This means that mathematics, created by the ancient Greeks, and their doctrine of Nature, based on mathematical and “harmonic” principles, are one and the same scientific objects. Euclid’s Elements, written in the III c. BC, is the most striking embodiment of the process of the “Mathematization of Harmony” in the ancient Greece
5. Proclus’ Hypothesis
5.1. What Was the Purpose of Euclid to Create His Elements?
At first glance, it seems that the answer to this question is very simple: The main objective of Euclid was to present the main achievements of the Greek mathematicians 300 years before Euclid, using the “axiomatic method”. This view of the Elements is the most common in modern mathematics.
However, apart from “axiomatic” point of view, there is another point of view on Euclid’s motives in writing the Elements. This point of view is expressed by the Greek philosopher and mathematician Proclus Diadoxus (412-485), one of the first commentators of Euclid’s Elements.
Among Proclus’ mathematical works the “Commentary on the first book of Euclid’s Elements” is the most known. In his Commentary he suggested the following unusual hypothesis.
As is known, the Book XIII, that is, the final book of the Elements, is devoted to the geometric theory of the five regular polyhedra, which played a major role in Plato’s Cosmology and are known in modern science as Platonic solids. This fact drew Proclus’ attention. As pointed out by well-known Belarusian philosopher Eduard Soroko [2] , according to Proclus, Euclid “created the Elements not for the purpose to present geometry itself, but to give a full systematic theory for constructing the five ‘Platonic solids’, highlighting in passing some of the latest achievements of ancient Greeks’ mathematics.”
5.2. How Did Euclid Use the “Golden Section”?
The question arises: why Euclid introduced in the Elements different forms of the “golden ratio”, which we can find in the Books II, VI and XIII? To answer this question, we again return back to the Platonic solids (Figure 5). As is known, only three types of regular polygons can be the faces of the Platonic solids: equilateral triangle (tetrahedron, octahedron, icosahedron), square (cube) and a regular pentagon (dodecahedron). In order to construct the Platonic solids, we must, first of all, be able to build the faces of Platonic solids geometrically (that is, by using a ruler and compass).
Euclid knew, how to construct an equilateral triangle and a square, but he met some difficulties at constructing of the regular pentagon, which underlies the dodecahedron (Figure 11(a)). The icosahedron in Figure 11(b) is geometric figure dual to the dodecahedron.
![]()
![]() (a) (b)
(a) (b)
Figure 11. Dodecahedron (a) and icosahedron (b).
It is for this purpose, Euclid had introduced in the Book II the “golden ratio” (Proposition II.11), which is presented in the Elements in two forms. By using the “golden ratio”, Euclid constructs the “golden” isosceles triangle, whose angles at the base are equal to the doubled angle at the vertex (Figure 12(a)).
At first, we construct the “golden” isosceles triangle by using a ruler and compass (see Figure 12(a)). The triangle ABD has the equal sides AB and AD and the equal angles B and D at the base BD. These angles are equal to the doubled angle at the vertex A.
By using the “golden” isosceles triangle ABD (Figure 12(a)), we construct the regular pentagon in Figure 12(b).
And then we should do only one step to the geometric construction of the dodecahedron (Figure 11(a)), one of the most important regular polyhedra, which symbolized the Ether or Universal Mind in Plato’s cosmology.
Pentagon and pentagram. Note that the regular pentagon (Figure 13), which is the base of the dodecahedron, was very important geometric figure of Greek science because the golden ratio is a basis of the regular pentagon. The word of “pentagon” is derived from the Greek word of “pentagonon”.
If we draw in a pentagon all diagonals, then we get the pentagonal star, also known as a pentagram or pentacle. The name of “pentagram” is derived from the Greek word “pentagrammon” (pente―five and grammon― line).
It is proved that the points F, G, H, K, L of the intersection of pentagon’s diagonals are always the points of the golden ratio. At the same time, they form a new regular pentagon FGHKL. In the new pentagon we can draw new diagonals. The points of their intersection adduce to the new regular pentagon and this process can be continued indefinitely. Thus, the pentagon ABCDE consists of an infinite number of regular pentagons, which are formed each time by the points of the diagonals intersection. This endless repetition of the same geometric figure (the regular pentagon) creates a sense of rhythm and harmony, which is fixed by our unconscious mind.
The Pythagoreans were delighted with the pentagram, which was considered as their main distinctive symbol.
5.3. Three “Key” Problems of the Ancient Mathematics
The prominent Russian mathematician academician Kolmogorov in the book [13] had identified the two main,
![]()
![]() (a) (b)
(a) (b)
Figure 12. The “golden” isosceles triangle (a) and the pentagon (b).
![]()
Figure 13. The regular pentagon and pentagram.
that is, “key” problems, which stimulated the development of mathematics at the stage of its origin: the counting problem and the measurement problem. However, it follows from “Proclus’ hypothesis” that one more “key” problem, the problem of harmony, which underlies Euclid’s Elements, stimulated the development of mathematics at the stage of its origin.
Thus, not two but three “key” problems, the counting problem, the measurement problem, and the harmony problem, underlie mathematics at the stage of its origin (see Figure 14).
The first two “key” problems resulted in the creation of two fundamental notions of mathematics―natural number and irrational number, which underlie the Classical Mathematics. The problem of harmony, connected with the division of line segment in extreme and mean ratio (the “golden ratio”) (Proposition II.11 of Euclid’s Elements) resulted in the Mathematics of Harmony, which is interpreted now as a new interdisciplinary direction of contemporary science and mathematics [3] .
This approach is unexpected for many mathematicians. It turns out, that in parallel with the Classical Mathematics, another mathematical direction, the Mathematics of Harmony, was developing in mathematics starting since ancient science.
Similarly to the Classical Mathematics, the Harmony Mathematics takes its origin in Euclid’s Elements. However, the Classical Mathematics focuses on the axiomatic approach and other ancient achievements (number theory, theory of irrationalities and so on), while the Mathematics of Harmony is based on the golden ratio (Proposition II.11) and Platonic solids, described in Book XIII of Euclid’s Elements. Thus, Euclid’s Elements is a source of the two independent mathematical directions: the Classical Mathematics and the Mathematics of Harmony.
5.4. The Historical Significance of Proclus’ Hypothesis for Mathematics
The main conclusion from Proclus’ hypothesis consists in the fact that Euclid’s Elements, the greatest Greek mathematical work, was written by Euclid under the direct influence of the ancient idea of Harmony, which was associated with the Platonic solids.
Thus, the Proclus’ hypothesis allows suggesting that the well-known in the ancient science Pythagorean doctrine of numerical harmony of the Universe and Plato’s cosmology, based on regular polyhedra, were embodied in the greatest mathematical work of Greek mathematics, Euclid’s Elements.
From this reasoning’s, we can consider Euclid’s Elements as the first attempt to create the “Mathematical Theory of the Universe Harmony”, associated in ancient science with Platonic solids. This is the main secret of Euclid’s Elements that leads us to the revision of the history of the mathematics, starting since Euclid.
![]()
Figure 14. Three “key” problems of the ancient mathematics.
5.5. A Role of the Mathematics of Harmony for School Mathematical Education
For many centuries, the creation of the Classical Mathematics, the Tsarina of science, was the main focus of mathematicians. However, starting from Pythagoras, Plato, Euclid, Fibonacci, Pacioli, Kepler, the intellectual forces of many prominent mathematicians and thinkers were directed towards the development of the basic concepts and applications of the Mathematics of Harmony. We don’t have a right to ignore this important historical fact.
Unfortunately, these two important mathematical directions (Classical Mathematics and Mathematics of Harmony) evolved separately from one another. A time came to unite these important mathematical directions. This unusual union can lead to new scientific discoveries in mathematics and theoretical natural sciences.
A new approach to the origin of mathematics (see Figure 11) is very important for school mathematical education. The prominent Ukrainian mathematician academician Yuri Mitropolsky (Figure 15) wrote in his review [14] :
“One may wonder what place in the general theory of mathematics is occupied by Mathematics of Harmony created by Prof. Stakhov? It seems to me, that in the last centuries, as Nikolay Lobachevsky said, ‘mathematicians turned all their attention to the Advanced Parts of Analytics, neglecting the origins of Mathematics and not willing to dig the field that already been harvested by them and left behind.’ As a result, this created a gap between ‘Elementary Mathematics’―basis of modern mathematical education, and ‘Advanced Mathematics’. In my opinion, the Mathematics of Harmony developed by Prof. Stakhov fills up that gap. i.e, ‘Mathematics of Harmony’ is a big theoretical contribution, first of all to the development of ‘Elementary Mathematics’ and as such should be considered of great importance for mathematical education.”
Mitroplsky’s proposal introduces, in very natural manner, the idea of harmony and the golden ratio into school mathematical education. This provides for pupils the natural access to ancient science and to its main achievement―the idea of Harmony―and to tell them about the most important architectural and sculptural works of the ancient arts based upon the golden ratio (including pyramid of Khufu (Cheops), Nefertiti, Parthenon, Doryphoros, Venus and so on).
5.6. A Discussion of Proclus’ Hypothesis in the Historical-Mathematical Literature
The analysis of Proclus’ hypothesis is found in many mathematical sources. Consider some of them [15] -[17] . In the book [15] we read: “According to Proclus, the main objective of the ‘Elements’ was to present the geometric construction of the so-called Platonic solids.”
![]()
Figure 15. Academician Yuri Mitropolsky (1917-2008).
In the book [16] , this idea got a further concrete development: “Proclus, by mentioning all previous mathematicians of Plato’s circle, said: Euclid lived later than the mathematicians of Plato’s circle, but earlier than Eratosthenes and Archimedes... He belonged to Plato’s school and was well acquainted with Plato’s philosophy and his cosmology; that’s why he put a creation of the geometric theory of the so-called Platonic solids as the main purpose of the Elements.”
This comment is very important and draws our attention to the connection of Euclid with Plato. Euclid fully shared Plato’s philosophy and cosmology, based on Platonic solids, that is why, Euclid put forward the creation of the geometric theory of Platonic solids as the main purpose of the Elements.
In the book [17] , there is discussed the influence of Plato and Euclid’ ideas on Johannes Kepler at designing of Kepler’s Cosmic Cup (Figure 16) in his first book “Mysterium Cosmographicum”:
“Kepler’s project in ‘Mysterium Cosmographicum’ was to give ‘true and perfect reasons for the numbers, quantities, and periodic motions of celestial orbits.’ The perfect reasons must be based on the simple mathematical principles, which had been found by Kepler in the Solar system, by using multiple geometric demonstrations. The general scheme of his model was borrowed by Kepler from Plato’s Timaeus, but the mathematical relations for the Platonic solids (pyramid, cube, octahedron, dodecahedron, icosahedron) were taken by Kepler from the works by Euclid and Ptolemy. At that, Kepler followed to Proclus and believed that ‘the main goal of Euclid was to build a geometric theory of the so-called Platonic solids.’ Kepler was completely fascinated by Proclus, he often quotes him and calls him ‘Pythagorean’.”
From this quote, we can conclude that Kepler used the Platonic solids to create the Cosmic Cup, but all the mathematical relations for the Platonic solids were borrowed by him from Book XIII of the Elements, that is, he united in his studies Plato’s Cosmology with Euclid’s Elements. At that, he fully believed in Proclus’ hypothesis that the main goal of Euclid was to give the complete geometric theory of Platonic solids, which were used by Kepler in his geometric model of the Solar system (Figure 16).
5.7. Icosahedron as the Main Geometrical Object of Mathematics
In the late of the 19th century, the great German mathematician Felix Klein (Figure 17) drew attention to the Platonic solids. He predicted an outstanding role of the Platonic Solids, in particular, the icosahedron for the future development of science and mathematics. In 1884 Felix Klein published the book “Lectures on the Icosahedron” [18] , dedicated to the geometric theory of the icosahedron.
According to Klein, the tissue of mathematics widely and freely extends like the sheets of the different mathematical theories. But there are geometric objects, which unites many mathematical theories. Their geometry binds these mathematical theories and allows embracing a general mathematical sense of the miscellaneous theories. In Klein’s opinion, the icosahedron is precisely such mathematical object. Klein treats the regular
![]()
Figure 16. “Cosmic Cup”―Kepler’s model of the Solar system based on Platonic solids.
icosahedron as the mathematical object, from which the branches of the five mathematical theories follow, namely, geometry, Galois’ theory, group theory, invariants theory and differential equations.
Thus, the prominent mathematician Felix Klein after Pythagoras, Plato, Euclid, and Johannes Kepler could estimate a fundamental role of the Platonic Solids, in particular, of the icosahedron, for the development of science and mathematics. Klein’s main idea is extremely simple [18] : “Each unique geometrical object is somehow or other connected to the properties of the regular icosahedron”.
Unfortunately, Klein’s contemporaries could not understand and appreciate a revolutionary importance of Klein’s idea, suggested by him in 19th century. However, its significance was appreciated one century after, when the Israeli scientist Dan Shechtman discovered in 1982 a special alloy called quasi-crystals and the outstanding researchers Robert F. Curl, Harold W. Kroto and Richard E. Smalley discovered in 1985 a special kind of carbon called fullerenes. It is important to emphasize that the quasi-crystals are based on the Platonic icosahedron and the fullerenes on the Archimedean truncated icosahedron. This means that Felix Klein in the 19th century made a brilliant prediction of the two outstanding scientific discoveries of modern science: fullerenes (Nobel Prize in chemistry-1996) and quasi-crystals (Nobel Prize in chemistry-2011).
6. Conclusions
1) For several millennia the prominent thinkers and scientists: Pythagoras, Plato, Euclid, Fibonacci, Pacioli, Kepler, Binet, Lucas, Klein, and in the 20th century Coxeter, Vorobyev, Hoggatt, Vajda and other famous mathematicians participated in the development of the “Mathematics of Harmony”.
2) It is clear that, if the truth will prevail and Proclus’ hypothesis will be recognized by modern historians of mathematics as it was done in [15] -[17] , it will be a prerequisite for the introduction of the Ancient Concept of Harmony into modern mathematics and mathematical education.
3) In this case, the Idea of Harmony introduces into mathematics the main applied goal, for which the ancient Greeks have created the Mathematical Theory of Nature [12] , namely, the creation of the useful mathematical models of the Universe Harmony.
4) It is clear that Platonic solids, “golden section”, Fibonacci numbers and their generalizations should underlie these models [3] . These outstanding mathematical discoveries of ancient and medieval mathematics should no longer play the role of a sort of “rogue” in mathematics and mathematical education and they will occupy here the worthy place, which they certainly deserve.
5) This process, which is named in [19] the “Harmonization of Mathematics” and has been embodied in author’s book “The Mathematics of Harmony” (World Scientific, 2009) [3] , can become the beginning of the “golden” revolution in mathematics and can lead to the merger of mathematics with theoretical natural sciences. Morris Klain in the final chapter, “The Authority of Nature,” of his wonderful book [12] is proclaiming this goal.