Three Generations of Particles Are Necessary for Our Universe as Well as the Next Level of Matter ()
1. Introduction
We have not a good explanation why in the Standard model three generations of particles with the same properties take place. We have not a good understanding from which particles of dark matter is made. Till now we do not sure, that quarks, leptons and gauge bosons are fundamental particles. If observable elementary particles are composite particles then these and a part of other problems of cosmology may be solved. The first generation of particles gives the whole observable world. The second and third generations (their existence) are responsible to dark matter (the latest reviews on dark matter can be found in papers [1] -[3] ). Structuring of dark matter and the consequent structuring of the baryon component of our Universe produced of particles (familons) that originated if one considers the horizontal symmetry among generations. For opportunity of structuring of the Universe at least three generations of particles are necessary compulsorily. Only in the preon model of elementary particles the fractality in the distribution of material components of the Universe is a natural phenomenon caused by phase transitions [4] . The inevitable of phase transitions is evidently during the Universe evolution (a sharp downfall of temperature after it birth). Also the preon model provides a natural explanation of dark matter which may consist of pseudo-Goldstone bosons of familon type with a mass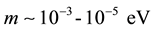 . In a medium of familons created by the upper and lower quarks of different generations and leptons must be phase transitions at different temperatures leading to formation of “distinguished scales” in the Universe to the fractal distribution. Owing to gravitation, the baryonic component repeated this picture forming galaxies, clusters and super-clusters of galaxies.
. In a medium of familons created by the upper and lower quarks of different generations and leptons must be phase transitions at different temperatures leading to formation of “distinguished scales” in the Universe to the fractal distribution. Owing to gravitation, the baryonic component repeated this picture forming galaxies, clusters and super-clusters of galaxies.
The observational data tell us that at least the baryon large-scale structure has formed at a red shift z ~ 6 - 8 or even earlier [5] . For the standard ΛCDM model, the existence of structures at such red shifts is the difficulty because there is too little time for the primordial perturbations to develop into observable structures against the background of the expanding Universe. And, if baryonic structures have formed at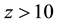 , then a key role in such process may play dark matter particles which prepared the medium for baryon condensation. In the standard cosmological model, one of the DM components is light perfect gas particles with masses
, then a key role in such process may play dark matter particles which prepared the medium for baryon condensation. In the standard cosmological model, one of the DM components is light perfect gas particles with masses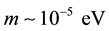 , practically not interacting with the particles of usual matter. They are called axions. These particles have not yet been discovered due to their super weak interaction with baryons and leptons. There is another likely component of “cold” dark matter: neutralinos. Neutrinos make a “hot” dark matter component. Dark matter particles, familons in our case (familons are a kind of axions), at a certain stage of the Universe evolution, as a result of relativistic phase transitions, lost their residual U(1) symmetry and formed a large-scale structure of dark matter, i.e., prepared the medium for baryon condensation. In other words, the dark matter particles, “homogeneously” filling space, in a result of phase transitions formed a certain structure, which we call, in the case of baryons, the large-scale structure of the Universe. Density perturbations in dark matter had a fractal nature because only a critical phenomenon (phase transition) could create a fractal nature in the distribution of density fluctuations. And, if a fractal nature of the baryonic large-scale structure is ultimately proved, then our model can become a basic model explaining this phenomenon. Thus, besides the fractal distribution of material components of the Universe, three generations of elementary particles and distinguished scales in the Universe indicate on a more deep level of matter. In this publication, we want to show this. Of course, many people try to follow this trend [6] [7] since any reasons are absent to descent to the next level of fundamentality. Besides, our interest to the preon model of elementary particles is related as to the important cosmological consequences as and to the HERA experiment [8] [9] , whose result is interpreted as a lepto-quark resonance (although there is another interpretation of this experiment). Note that according to inflationary theory, all elementary particles populating the Universe were created during the process of reheating of the Universe after inflation. After inflation, the scalar field
, practically not interacting with the particles of usual matter. They are called axions. These particles have not yet been discovered due to their super weak interaction with baryons and leptons. There is another likely component of “cold” dark matter: neutralinos. Neutrinos make a “hot” dark matter component. Dark matter particles, familons in our case (familons are a kind of axions), at a certain stage of the Universe evolution, as a result of relativistic phase transitions, lost their residual U(1) symmetry and formed a large-scale structure of dark matter, i.e., prepared the medium for baryon condensation. In other words, the dark matter particles, “homogeneously” filling space, in a result of phase transitions formed a certain structure, which we call, in the case of baryons, the large-scale structure of the Universe. Density perturbations in dark matter had a fractal nature because only a critical phenomenon (phase transition) could create a fractal nature in the distribution of density fluctuations. And, if a fractal nature of the baryonic large-scale structure is ultimately proved, then our model can become a basic model explaining this phenomenon. Thus, besides the fractal distribution of material components of the Universe, three generations of elementary particles and distinguished scales in the Universe indicate on a more deep level of matter. In this publication, we want to show this. Of course, many people try to follow this trend [6] [7] since any reasons are absent to descent to the next level of fundamentality. Besides, our interest to the preon model of elementary particles is related as to the important cosmological consequences as and to the HERA experiment [8] [9] , whose result is interpreted as a lepto-quark resonance (although there is another interpretation of this experiment). Note that according to inflationary theory, all elementary particles populating the Universe were created during the process of reheating of the Universe after inflation. After inflation, the scalar field  (inflaton) oscillates near the minimum of its effective potential and produces elementary particles. This process completes when all (or almost all) the energy of the classical scalar field
(inflaton) oscillates near the minimum of its effective potential and produces elementary particles. This process completes when all (or almost all) the energy of the classical scalar field 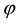 transfers to the thermal energy of elementary particles [10] .
transfers to the thermal energy of elementary particles [10] .
2. The Preon Structures of Particles
12 known elementary particles (or 24 with antiparticles) display their own repeated picture giving a reason to suppose that they are not truly fundamental but consist of still smaller particles (preons). The Standard model postulates the existence of two classes of indivisible particles: fermions and bosons. Fermions are quarks and leptons (spin 1/2), while gauge bosons (spin 0) are particles―carriers of forces between interacting fermions. In 2012 we witnessed the discovery of the Higgs boson at the Large Hadron Collider (LHC) [11] [12] , it was the last missing link of the Standard model. Table 1, which contains the fermions and gauge bosons, has a meaning similar to that of Mendeleev’s table of chemical elements. It contains three columns showing three generations of particles. It is important to note that experiments have revealed decays of heavier quarks into the lightest ones 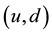 since in the second and third generations the quarks are heavier than in the first one, and in the third generation
since in the second and third generations the quarks are heavier than in the first one, and in the third generation 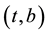 they are heavier than in the second one
they are heavier than in the second one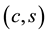 . The electron also has heavier partners, the muon
. The electron also has heavier partners, the muon  and the taon
and the taon 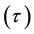 which are much heavier than the electron; in addition, there are three sorts of rather light uncharged neutrinos, and one can speak of decays of heavier leptons into lighter ones
which are much heavier than the electron; in addition, there are three sorts of rather light uncharged neutrinos, and one can speak of decays of heavier leptons into lighter ones , but such decays have not yet been observed.
, but such decays have not yet been observed.
The limits on the neutrino masses as well as the masses of all particles have been taken from [13] . Following [14] [15] , let us suppose that there are preons of two types: preon “+” with the electric charge +1/3 and preon “0”, without an electric charge. An antipreon “−” has the electric charge −1/3, and a neutral antipreon will be designated as “□”. Then the whole set of elementary particles can be described in the preon version according to Table 2.
A natural question emerges: why does one need three generations of particles while it would be sufficient to have only the first one, whose particles give rise to the whole baryonic component of the Universe? It is somehow implicitly assumed that the second and third generations of particles are excited states of those of the first generation. Besides, particles of the second and third generations are unstable, i.e., they consist of combinations of the same preons and antipreons as and the particles of the first generation. Let us note that both preons and
![]()
Table 1. Standard model of elementary particles.
![]()
Table 2. The preon composition of elementary particles.
antipreons are fermions. From Table 2 it is evident that all elementary particles consist of three preons while the interaction carriers (gauge bosons) of six preons, and at that the 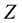 boson can consist of four combinations of preons. The same building blocks can form gluons, strong interaction carriers. A hint that quarks and leptons are composite particles can be seen in the radioactivity, when a nucleus decays into another nucleus, emitting charged particles and gamma quanta. We have only discussed the preon composition of particles of the first generation, and if those of the second and third generations are excitations of the first generation, then, with some limitations, one can agree that a certain mechanism connects the preons with each other in such way that activates the formation of a diversity of particles from the same initial blocks. Such a “declaration” is certainly nonphysical because the problem of generations is not yet quite clear. Let us note that the preons may have an electric charge equal to 1/6 rather than 1/3, and the quarks and leptons may consist of 5 preons. However, preons have not been observed experimentally (though there were such attempts). In the Standard model of particle physics, quarks, leptons and gauge bosons are point objects, having no internal structure of their own. It is implied that they have zero size. On the other hand, we know that protons and neutrons have a size of
boson can consist of four combinations of preons. The same building blocks can form gluons, strong interaction carriers. A hint that quarks and leptons are composite particles can be seen in the radioactivity, when a nucleus decays into another nucleus, emitting charged particles and gamma quanta. We have only discussed the preon composition of particles of the first generation, and if those of the second and third generations are excitations of the first generation, then, with some limitations, one can agree that a certain mechanism connects the preons with each other in such way that activates the formation of a diversity of particles from the same initial blocks. Such a “declaration” is certainly nonphysical because the problem of generations is not yet quite clear. Let us note that the preons may have an electric charge equal to 1/6 rather than 1/3, and the quarks and leptons may consist of 5 preons. However, preons have not been observed experimentally (though there were such attempts). In the Standard model of particle physics, quarks, leptons and gauge bosons are point objects, having no internal structure of their own. It is implied that they have zero size. On the other hand, we know that protons and neutrons have a size of 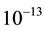 cm, but what is the true size of the quarks and leptons we do not know, and if we learn that, it will be possible to directly judge about their internal structure. These are the nearest tasks at the LHC and Fermilab. Besides, an internal structure of quarks, leptons and gauge bosons would be indicated by a discovery of, firstly, the fourth generation of particles, and, secondly, rare decays of the leptons
cm, but what is the true size of the quarks and leptons we do not know, and if we learn that, it will be possible to directly judge about their internal structure. These are the nearest tasks at the LHC and Fermilab. Besides, an internal structure of quarks, leptons and gauge bosons would be indicated by a discovery of, firstly, the fourth generation of particles, and, secondly, rare decays of the leptons  as well as some fine experiments (a measurement of the muon’s magnetic moment and others [13] ). Upgrading of the LHC in 2014 will lead to an increased energy of the proton beam, which will increase the number of detected collisions by a factor of 5. This will bring us to smaller scales, and what is required for a preon search. Formally, even a subpreon model can be realized, where preons themselves are composite particles [16] .
as well as some fine experiments (a measurement of the muon’s magnetic moment and others [13] ). Upgrading of the LHC in 2014 will lead to an increased energy of the proton beam, which will increase the number of detected collisions by a factor of 5. This will bring us to smaller scales, and what is required for a preon search. Formally, even a subpreon model can be realized, where preons themselves are composite particles [16] .
3. A General Discussion and Structure of the Preon Vacuum
Here we would like to study in more detail the structure of the preon nonperturbative vacuum emerging as a result of a correlation of non-Abelian fields at two scales![]() , the scale of metacolor confinement, and 150 MeV, the quantum chromodynamics scale). In [17] we have revealed that in the excitation spectrum of the nonperturbative preon vacuum there are pseudo-Goldstone modes. A spontaneous breakdown of the horizontal symmetry of quark-lepton generations results in emergence of familons. We consider these particles as the basic component of dark matter. A distinguishing feature of these particles is the existence of a residual U(1) symmetry and the opportunity of its spontaneous breakdown at
, the scale of metacolor confinement, and 150 MeV, the quantum chromodynamics scale). In [17] we have revealed that in the excitation spectrum of the nonperturbative preon vacuum there are pseudo-Goldstone modes. A spontaneous breakdown of the horizontal symmetry of quark-lepton generations results in emergence of familons. We consider these particles as the basic component of dark matter. A distinguishing feature of these particles is the existence of a residual U(1) symmetry and the opportunity of its spontaneous breakdown at ![]() as a result of a relativistic phase transition.In a phenomenological framework, one can assume that the values of primordial fluctuations of dark matter are not related to CMB fluctuations. In this case, in principle, the choice of initial values of dark matter fluctuations can be provided by any moment for the structure formation. The authors of articles [18] [19] considered dark matter as a gas of pseudo-Goldstone bosons, in which it is possible to have a phase transition at super low temperatures as compared to the collider temperatures. A strong nonlinearity was also supposed, that is, the dark matter particles should strongly interact with each other. Pseudo-Goldstone bosons emerge as particles as a result of breaking the continuous symmetry of vacuum. Four kinds of pseudo-Goldstone boson are distinguished: axions, arions, familons, and majorons. The small mass of pseudo-Goldstone bosons manifests itself as a result of a super weak interaction of Goldstone fields with nonperturbative vacuum condensates. The values of these masses are constrained by astrophysical and laboratory data [20] [21] :
as a result of a relativistic phase transition.In a phenomenological framework, one can assume that the values of primordial fluctuations of dark matter are not related to CMB fluctuations. In this case, in principle, the choice of initial values of dark matter fluctuations can be provided by any moment for the structure formation. The authors of articles [18] [19] considered dark matter as a gas of pseudo-Goldstone bosons, in which it is possible to have a phase transition at super low temperatures as compared to the collider temperatures. A strong nonlinearity was also supposed, that is, the dark matter particles should strongly interact with each other. Pseudo-Goldstone bosons emerge as particles as a result of breaking the continuous symmetry of vacuum. Four kinds of pseudo-Goldstone boson are distinguished: axions, arions, familons, and majorons. The small mass of pseudo-Goldstone bosons manifests itself as a result of a super weak interaction of Goldstone fields with nonperturbative vacuum condensates. The values of these masses are constrained by astrophysical and laboratory data [20] [21] :
![]() (1)
(1)
An astrophysical estimate has been obtained from the assumption that pseudo-Goldstone bosons affect the Universe expansion dynamics. The emergence of massive terms in the Goldstone field Lagrangian corresponds, in the formal mathematical sense, to the emergence of mass of pseudo-Goldstone bosons. Depending on the type of these particles and on the nonperturbative vacuum structure, the massive term can emerge both with a “correct” and an “incorrect” sign. This sign predetermines the fate of a residual symmetry of the pseudo-Goldstone fields. In the case of the “incorrect sign”, at low temperatures![]() , a Goldstone condensate inevitably forms, and then the symmetry of the vacuum state is broken spontaneously. The condensate emergence at
, a Goldstone condensate inevitably forms, and then the symmetry of the vacuum state is broken spontaneously. The condensate emergence at ![]() or at lower temperatures is a relativistic phase transition from a highly symmetric phase to a lower symmetric phase of the pseudo-Goldstone boson gas. We note that the general theory of cosmological phase transitions was formulated by D.A. Kirzhnitz and A.D. Linde as early as in the 80 s. The familon symmetry breakdown manifests itself in the different values of particle masses in the three generations. Some models have been suggested (see, e.g., [19] ), where the familon symmetry is a horizontal symmetry broken by a Higgs condensate. This hypothesis is natural since it is based on the general idea of unification of all particle interactions. An important issue for us is the fact that familons possess a residual U(1) symmetry which takes place if some Goldstone degrees of freedom are not transferred to vector states. The properties of any pseudo-Goldstone bosons (as well as pseudo-Goldstone bosons of familon type) depend on the realization function of the Goldstone modes. These modes can emerge from the fundamental Higgs fields, as has been already suggested in [19] , as well as from collective excitations of a heterogeneous nonperturbative vacuum condensate, which is in our case more complicated than the quark-gluon condensate. The second opportunity is realized in theories where leptons, quarks and gauge bosons are composite objects, i.e., in the preon model of elementary particles. The phase transition in the cosmological familon gas is a 1st order phase transition with wide temperature range of phase coexistence. A numerical simulation of such relativistic phase transition has shown that a spatial interchange of high-symmetry and low-symmetry phases took place in the Universe with the density contrast
or at lower temperatures is a relativistic phase transition from a highly symmetric phase to a lower symmetric phase of the pseudo-Goldstone boson gas. We note that the general theory of cosmological phase transitions was formulated by D.A. Kirzhnitz and A.D. Linde as early as in the 80 s. The familon symmetry breakdown manifests itself in the different values of particle masses in the three generations. Some models have been suggested (see, e.g., [19] ), where the familon symmetry is a horizontal symmetry broken by a Higgs condensate. This hypothesis is natural since it is based on the general idea of unification of all particle interactions. An important issue for us is the fact that familons possess a residual U(1) symmetry which takes place if some Goldstone degrees of freedom are not transferred to vector states. The properties of any pseudo-Goldstone bosons (as well as pseudo-Goldstone bosons of familon type) depend on the realization function of the Goldstone modes. These modes can emerge from the fundamental Higgs fields, as has been already suggested in [19] , as well as from collective excitations of a heterogeneous nonperturbative vacuum condensate, which is in our case more complicated than the quark-gluon condensate. The second opportunity is realized in theories where leptons, quarks and gauge bosons are composite objects, i.e., in the preon model of elementary particles. The phase transition in the cosmological familon gas is a 1st order phase transition with wide temperature range of phase coexistence. A numerical simulation of such relativistic phase transition has shown that a spatial interchange of high-symmetry and low-symmetry phases took place in the Universe with the density contrast![]() . In the phase coexistence period [17] , the characteristic scale of such block-phase structure is determined by the horizon size at the time of the relativistic phase transition, i.e., in other words, there forms a large-scale structure of dark matter. To explain the hierarchy of baryonic structures, our model realizes at least three relativistic phase transitions. For the numerical agreement of our model with the observable data it is necessary to assume that relativistic phase transitions took place in dark matter in the post-recombination epoch at
. In the phase coexistence period [17] , the characteristic scale of such block-phase structure is determined by the horizon size at the time of the relativistic phase transition, i.e., in other words, there forms a large-scale structure of dark matter. To explain the hierarchy of baryonic structures, our model realizes at least three relativistic phase transitions. For the numerical agreement of our model with the observable data it is necessary to assume that relativistic phase transitions took place in dark matter in the post-recombination epoch at![]() . We have already mentioned that the familon symmetry breakdown is only indicated by the quark and lepton mass splitting, i.e., a discussion on familon production should be reduced to a discussion of the origin of particle masses. There are two mechanisms of mass generation: the Higgs mechanism (where the masses emerge due to an interaction between chiral fermion fields with a c-number Higgs condensate which is linear on the scalar field), and an essentially nonperturbative mechanism, in which mass generation is a result of an interaction of fermion fields with vacuum condensates of quark-gluon type (in the simplest case they are quadratic on the fields). In quantum chromodynamics the second mechanism is connected with the emergence of masses of the u and d-quarks. The numerical values of the gluon and quark condensates are known from the experimental data [18] :
. We have already mentioned that the familon symmetry breakdown is only indicated by the quark and lepton mass splitting, i.e., a discussion on familon production should be reduced to a discussion of the origin of particle masses. There are two mechanisms of mass generation: the Higgs mechanism (where the masses emerge due to an interaction between chiral fermion fields with a c-number Higgs condensate which is linear on the scalar field), and an essentially nonperturbative mechanism, in which mass generation is a result of an interaction of fermion fields with vacuum condensates of quark-gluon type (in the simplest case they are quadratic on the fields). In quantum chromodynamics the second mechanism is connected with the emergence of masses of the u and d-quarks. The numerical values of the gluon and quark condensates are known from the experimental data [18] :
![]() (2)
(2)
The main characteristic of quantum-chromodynamic vacuum is the gluon condensate, representing nonperturbative fluctuations of the gluon fields emerging in the processes of gluon vacuum tunneling between states degenerate by energy but possessing different quantum numbers. Fluctuations of the initially massless quark fields are induced, they appear as a response of the vacuum quark fields to gluon field fluctuations. The masses of heavy![]() ,
, ![]() ,
, ![]() ,
, ![]() quarks do not have a similar interpretation in the framework of quantum chromodynamics. Therefore, to explain the mass spectrum of heavy quarks, it is necessary to invoke additional physical arguments. These masses can be introduced phenomenologically by using the Higgs mechanism of mass generation but there is one more opportunity, which we would like to consider. The research groups H1 and ZEUS, working at the HERA collider, have reported, independently of each other, the discovery of a leptoquark with the mass
quarks do not have a similar interpretation in the framework of quantum chromodynamics. Therefore, to explain the mass spectrum of heavy quarks, it is necessary to invoke additional physical arguments. These masses can be introduced phenomenologically by using the Higgs mechanism of mass generation but there is one more opportunity, which we would like to consider. The research groups H1 and ZEUS, working at the HERA collider, have reported, independently of each other, the discovery of a leptoquark with the mass ![]() [8] [9] . One of possible explanations of its existence is given by the preon theory. Consider the simplest boson-fermion-preon model of left chiral quarks and leptons. The basic elements of this model are the chiral fermion preons
[8] [9] . One of possible explanations of its existence is given by the preon theory. Consider the simplest boson-fermion-preon model of left chiral quarks and leptons. The basic elements of this model are the chiral fermion preons![]() ,
, ![]() and the scalar preons of quark
and the scalar preons of quark ![]() type and lepton
type and lepton ![]() type. In this model, the internal structure of elementary particles is
type. In this model, the internal structure of elementary particles is
![]() (3)
(3)
In the leptoquark case our model gives
![]() (4)
(4)
Here and henceforth ![]() is the color index of quantum chromodynamics,
is the color index of quantum chromodynamics, ![]() ,
, ![]() ,
, ![]() , 2, 3;
, 2, 3;![]() ,
, ![]() ,
, ![]() , 2, 3 is the number of quark and lepton generations,
, 2, 3 is the number of quark and lepton generations, ![]() is the metacolor index, corresponding to the new metachromodynamic interaction that connects preons into quarks and leptons. Inside quarks and leptons, the metagluonic fields
is the metacolor index, corresponding to the new metachromodynamic interaction that connects preons into quarks and leptons. Inside quarks and leptons, the metagluonic fields ![]() and the scalar preon fields are in the state of confinement. This effect is similar by its physical nature to the confinement of quarks and gluons inside hadrons, providing the existence of nonperturbative metagluonic and preon condensates. These condensates are described by the following relations:
and the scalar preon fields are in the state of confinement. This effect is similar by its physical nature to the confinement of quarks and gluons inside hadrons, providing the existence of nonperturbative metagluonic and preon condensates. These condensates are described by the following relations:
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Here ![]() is the energy scale of preon confinement,
is the energy scale of preon confinement, ![]() nd
nd ![]() are the condensate matrices. The condensates (5) and (6), together with the gluonic condensates
are the condensate matrices. The condensates (5) and (6), together with the gluonic condensates ![]() and the quark condensates
and the quark condensates ![]() provide a quark mass creation mechanism for all three particle generations. In [17] , we have illustrated the mass creation mechanism for all three particle generations by a special figure. Here we would like to elucidate that in the matrices in which additional indexes are included (see [17] )
provide a quark mass creation mechanism for all three particle generations. In [17] , we have illustrated the mass creation mechanism for all three particle generations by a special figure. Here we would like to elucidate that in the matrices in which additional indexes are included (see [17] )
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
for the sake of simplicity, the gluon and metagluon condensates, playing the role of sources of nonperturbative preon fluctuations, are not indicated. In the process of mass creation of the upper quarks of the 2nd and 3rd generations, the element (8) of this structure takes part. The element (9) takes part in the mass creation process for the lower quarks of the 2nd and 3rd generations, and the element (10) of this structure is necessary for mass creation in the 2nd and 3rd generations of charged leptons.
We proceed from the assumption that the first-generation quark masses are created according to the pure quantum chromodynamic mechanism. Formally mathematically, the matrices (8)-(10) are complex 2 × 2 matrices of a general form, that is, each of them contains eight numbers. We are considering in this case those vacuum states in which these matrices are parametrized by only two numbers, are real and diagonal. It is then easy to calculate that the number of parameters contained in the real diagonal matrices (8)-(10) is precisely equal to the number of particle masses in the 2nd and 3rd quark and lepton generations. Familons as physical objects are collective excitations of the heterogeneous nonperturbative condensates (8)-(10). The three types of nonperturbative condensates correspond to the three families of familon fields. Evidently the number of familons in a family is equal to 8, i.e., it coincides with the maximum number of parameters in the condensate matrices.
A very small (as compared to![]() ) rest mass of the Goldstone modes is gained due to interactions with the pure quark condensates, and they acquire in this case the status of pseudo-Goldstone bosons. In the framework of this theory, dark matter is a system of familon collective excitations of the heterogeneous nonperturbative vacuum. This system consists of three subsystems: familons of upper-quark type, familons of lower-quark type, and familons of lepton type. At stages of the cosmological evolution which are far from the quarkonization time and that of leptogenesis in the preon plasma
) rest mass of the Goldstone modes is gained due to interactions with the pure quark condensates, and they acquire in this case the status of pseudo-Goldstone bosons. In the framework of this theory, dark matter is a system of familon collective excitations of the heterogeneous nonperturbative vacuum. This system consists of three subsystems: familons of upper-quark type, familons of lower-quark type, and familons of lepton type. At stages of the cosmological evolution which are far from the quarkonization time and that of leptogenesis in the preon plasma![]() , heavy unstable familons are obviously already absent. At these stages, the familon subsystem is described by five field degrees of freedom. The fate of each subsystem of the low-energy familon gas crucially depends on the sign of the squared rest masses created by the interaction of familons with quark condensates. The idea on the physical nature of familons is unambiguously formalized in the field-theoretic model. For simplicity, let us consider the model of a single familon subsystem corresponding to the upper quarks of the second and third generations
, heavy unstable familons are obviously already absent. At these stages, the familon subsystem is described by five field degrees of freedom. The fate of each subsystem of the low-energy familon gas crucially depends on the sign of the squared rest masses created by the interaction of familons with quark condensates. The idea on the physical nature of familons is unambiguously formalized in the field-theoretic model. For simplicity, let us consider the model of a single familon subsystem corresponding to the upper quarks of the second and third generations![]() . A chiral nature of the quarks is a fact known from the experiment, and the symmetry group can be here only the chiral-familon group SU(2)L × SU(2)R . Familon excitations should be described by the 8-dimensional (by the number of components of the matrix (8)) reducible representation of this group, decomposed into two irreducible representations
. A chiral nature of the quarks is a fact known from the experiment, and the symmetry group can be here only the chiral-familon group SU(2)L × SU(2)R . Familon excitations should be described by the 8-dimensional (by the number of components of the matrix (8)) reducible representation of this group, decomposed into two irreducible representations ![]() and
and![]() , which differ from each other by the spatial parity sign. The model Lagrangian has the form:
, which differ from each other by the spatial parity sign. The model Lagrangian has the form:
![]() (11)
(11)
The terms with the mass parameters![]() ,
, ![]() have been introduced into (11) with “wrong” signs in order to provide a spontaneous breakdown of the familon symmetry at the metacolor confinement scale. The condensate contains mean values of the scalar fields (but not the pseudoscalar ones),
have been introduced into (11) with “wrong” signs in order to provide a spontaneous breakdown of the familon symmetry at the metacolor confinement scale. The condensate contains mean values of the scalar fields (but not the pseudoscalar ones),
![]() (12)
(12)
and this provides parity conservation in the strong interactions. A detailed study of the La-grangian (11) has shown that these vacuum mean values violate the original chiral familon symmetry up to the residual U(1) symmetry, i.e., SU(2)L × SU(2)R → U(1). The scalar field condensates (12) create, according to the structure of the two last terms in (11), a split spectrum of quark masses:
![]() (13)
(13)
As it is evident from Equations (13) for![]() ,
, ![]() the experimentally observed quark mass values
the experimentally observed quark mass values ![]() and
and ![]() are realized only at small values of the constants
are realized only at small values of the constants![]() ,
, ![]() of the quark-familon interactions. The smallness of these constants provides a hyperweak interaction of familons with usual matter. The preon model helps one to understand the cause of this smallness. As it is evident from Equations (6) and (7), the complex heterogeneous condensate, responsible for quark mass generation, emerges as a result of a correlation of fluctuating fields belonging to different levels. The chromodynamic fluctuations at the scale
of the quark-familon interactions. The smallness of these constants provides a hyperweak interaction of familons with usual matter. The preon model helps one to understand the cause of this smallness. As it is evident from Equations (6) and (7), the complex heterogeneous condensate, responsible for quark mass generation, emerges as a result of a correlation of fluctuating fields belonging to different levels. The chromodynamic fluctuations at the scale ![]() should be correlated with the metachromodynamic fluctuations at the scale of
should be correlated with the metachromodynamic fluctuations at the scale of ![]() . It is clear that the phenomenological constants
. It is clear that the phenomenological constants ![]() and
and ![]() are proportional to the probability of these correlations, and their smallness reflects the small probability of correlations at different scales of fluctuations. The equations for vacuum mean values, fixing a spontaneous break-down of the familon symmetry, contain the quark vacuum condensate:
are proportional to the probability of these correlations, and their smallness reflects the small probability of correlations at different scales of fluctuations. The equations for vacuum mean values, fixing a spontaneous break-down of the familon symmetry, contain the quark vacuum condensate:
![]() (14)
(14)
Equation (14) are used for separation of the quantum components of the familon fields from the Lagrangian (11). However, we are above all interested in the familon mass spectrum. The spontaneous breakdown of the SU(2)L × SU(2)R symmetry converts the six-parameter group into a single-parameter one. According to Goldstone’s theorem, five degrees of freedom must be practically massless at the scale of![]() , consequently, the full model must contain three heavy familons. Two of them are represented by the energy density perturbations of the condensates (12) and are described by orthogonal superpositions of the quantum components of the scalar fields
, consequently, the full model must contain three heavy familons. Two of them are represented by the energy density perturbations of the condensates (12) and are described by orthogonal superpositions of the quantum components of the scalar fields ![]() and
and![]() . The third heavy familon is identified with one of the two orthogonal superpositions of the pseudoscalar fields
. The third heavy familon is identified with one of the two orthogonal superpositions of the pseudoscalar fields ![]() and
and![]() . Let us now proceed to a description of the pseudo-Goldstone modes. They can be presented in the form of
. Let us now proceed to a description of the pseudo-Goldstone modes. They can be presented in the form of
1) a real pseudoscalar field with the mass
![]() (15)
(15)
2) a complex pseudoscalar field with the mass
![]() (16)
(16)
3) and a complex scalar field whose squared mass is negative
![]() (17)
(17)
These masses are estimated by order of magnitude as follows
![]() (18)
(18)
![]() (19)
(19)
Naturally these light pseudo-Goldstone particles should be contained in the composition of dark matter. As to the negative squared mass of the complex scalar field, it means that at low temperatures,
![]() (20)
(20)
the vacuum of pseudo-Goldstone particles is unstable, and in such vacuum, at a temperature ![]() a relativistic phase transition must take place, resulting in a state with a spontaneously broken residual U(1) symmetry. The other two familon subsystems are studied in a similar way. For the lower-quark familon subsystem we have
a relativistic phase transition must take place, resulting in a state with a spontaneously broken residual U(1) symmetry. The other two familon subsystems are studied in a similar way. For the lower-quark familon subsystem we have
![]() (21)
(21)
which means that this familon subsystem is also unstable at low temperatures, and at
![]() (22)
(22)
it should undergo a relativistic phase transition to a state with a spontaneously broken U(1) symmetry. The subsystem of leptonic familons has the same instability, and it undergoes a relativistic phase transition at ![]() though here we are facing the experimentally unstudied lepton condensates. From the mass formulas (15)-(17), (21) it follows that dark matter consisting of pseudo-Goldstone bosons of familon type is a multicomponent heterogeneous system evolving along a complicated thermodynamic way. The dark matter composition contains particles with 9 different rest masses. In the course of evolution, this system has undergone three relativistic phase transitions which took place at different temperatures. Thus, in dark matter consisting of pseudo-Goldstone bosons, there can be both a “hot” (relativistic) component consisting of massless particles of three types, and “cold” (non-relativistic) components consisting of massive particles.
though here we are facing the experimentally unstudied lepton condensates. From the mass formulas (15)-(17), (21) it follows that dark matter consisting of pseudo-Goldstone bosons of familon type is a multicomponent heterogeneous system evolving along a complicated thermodynamic way. The dark matter composition contains particles with 9 different rest masses. In the course of evolution, this system has undergone three relativistic phase transitions which took place at different temperatures. Thus, in dark matter consisting of pseudo-Goldstone bosons, there can be both a “hot” (relativistic) component consisting of massless particles of three types, and “cold” (non-relativistic) components consisting of massive particles.
4. Thermodynamics of a Phase Transition
It is appropriate to recall here that dark matter consisting of pseudo-Goldstone bosons of familon type has some specific properties: a super weak interaction with usual matter and a sufficiently strong interaction of the familons with each other. The reason is clear from qualitative arguments: the preon vacuum is a strongly nonlinear medium formed by strong chromodynamic and metachromodynamic interactions. Therefore, a large inherent nonlinearity of perturbations in this medium seems to be obvious, which provides a relativistic phase transition with spontaneous breakdown of the residual symmetry of familon fields and makes it possible to describe the relativistic phase transition using the thermodynamic method. Indeed, if the coupling constants ![]() in the Lagrangian (11) are not anomalously small, then the familon gas emerging in the course of cosmological evolution at the moment when there appear metachromodynamic and preon condensates, should rapidly relax to a thermodynamic equilibrium state. Of course, the thermodynamic temperature of the familon gas does not necessarily coincide with the thermodynamic temperature of all other subsystems of the Universe. In the modern epoch this fact can manifest itself in that the temperature of the familon gas as a part of dark matter can differ from the CMB temperature. Thus, the task is to construct the thermodynamics of a relativistic phase transition of the field system with the Lagrangian (11) using the methods of temperature quantum field theory. We have formulated the thermodynamics of the Lagrangian system (11) in the self-consistent field approximation in our paper [20] . The main problem is to build the non-equilibrium Landau functional, free energy density. For strongly nonlinear systems like the one under consideration, it is hard to write down the Landau functional in an explicit form. Implicitly, in the self-consistent field approximation, it is given by a functional depending on proper and improper values of the order parameters [20] . Fortunately, a calculation of all observed quantities and determination of the phase stability conditions can be carried out with the aid of a simpler functional which does not contain improper order parameters. The improper order parameters are represented by additional vacuum shifts of heavy familon fields induced by the proper order parameters η. This functional has the form
in the Lagrangian (11) are not anomalously small, then the familon gas emerging in the course of cosmological evolution at the moment when there appear metachromodynamic and preon condensates, should rapidly relax to a thermodynamic equilibrium state. Of course, the thermodynamic temperature of the familon gas does not necessarily coincide with the thermodynamic temperature of all other subsystems of the Universe. In the modern epoch this fact can manifest itself in that the temperature of the familon gas as a part of dark matter can differ from the CMB temperature. Thus, the task is to construct the thermodynamics of a relativistic phase transition of the field system with the Lagrangian (11) using the methods of temperature quantum field theory. We have formulated the thermodynamics of the Lagrangian system (11) in the self-consistent field approximation in our paper [20] . The main problem is to build the non-equilibrium Landau functional, free energy density. For strongly nonlinear systems like the one under consideration, it is hard to write down the Landau functional in an explicit form. Implicitly, in the self-consistent field approximation, it is given by a functional depending on proper and improper values of the order parameters [20] . Fortunately, a calculation of all observed quantities and determination of the phase stability conditions can be carried out with the aid of a simpler functional which does not contain improper order parameters. The improper order parameters are represented by additional vacuum shifts of heavy familon fields induced by the proper order parameters η. This functional has the form
![]() (23)
(23)
Here ![]() and
and ![]() are the effective masses of real pseudoscalar fields emerging in the low-symmetry phase at the decay of the complex
are the effective masses of real pseudoscalar fields emerging in the low-symmetry phase at the decay of the complex ![]() field (in the high-symmetry phase
field (in the high-symmetry phase![]() ),
), ![]() and
and ![]() are similar masses of the real scalar fields emerging in the low-symmetry phase at the decay of the complex field f (in the high-symmetry phase
are similar masses of the real scalar fields emerging in the low-symmetry phase at the decay of the complex field f (in the high-symmetry phase![]() ),
), ![]() is the effective mass of the real pseudoscalar field
is the effective mass of the real pseudoscalar field ![]()
![]() (24)
(24)
![]() , 2, 3,
, 2, 3, ![]() , 12, 3, 21, 22.
, 12, 3, 21, 22. ![]() are the characteristic integrals through which the observed quantities are expressed. All branches of the solutions to Equations (23) are tested for stability by the sufficient condition of a maximum:
are the characteristic integrals through which the observed quantities are expressed. All branches of the solutions to Equations (23) are tested for stability by the sufficient condition of a maximum:
![]() (25)
(25)
It has turned out that a solution for the low-symmetry phase exists in the temperature range![]() , i.e.,
, i.e., ![]() is the upper thermodynamic stability bound of the low symmetry phase. The same set of equations was independently integrated for the high-symmetry phase at
is the upper thermodynamic stability bound of the low symmetry phase. The same set of equations was independently integrated for the high-symmetry phase at![]() . We have found that the high- ymmetry phase exists at
. We have found that the high- ymmetry phase exists at![]() , i.e.,
, i.e., ![]() is the lower stability bound of the high-symmetry phase. Thus, the coexistence domain of the high- and low-symmetry phases is realized in the broad temperature range
is the lower stability bound of the high-symmetry phase. Thus, the coexistence domain of the high- and low-symmetry phases is realized in the broad temperature range ![]() (to see more detail in [20] ). The energy density dependences in the phase coexistence domain are shown in the Figure 1, where one can see that the equilibrium of phases in their coexistence domain is only possible with an abrupt density contrast. The cosmological familon gas evolves from the stability domain of the high-symmetry phase to the stability domain of the low-symmetry phase. The numerical modeling of this relativistic phase transition has shown that the average contrast of density in the block-phase structure
(to see more detail in [20] ). The energy density dependences in the phase coexistence domain are shown in the Figure 1, where one can see that the equilibrium of phases in their coexistence domain is only possible with an abrupt density contrast. The cosmological familon gas evolves from the stability domain of the high-symmetry phase to the stability domain of the low-symmetry phase. The numerical modeling of this relativistic phase transition has shown that the average contrast of density in the block-phase structure
![]()
Figure 1. The energy density as function of pressure in region of phase coexistence.
![]() . The size domains and masses of baryon and dark matter component inside domains depend on the value of the parameter
. The size domains and masses of baryon and dark matter component inside domains depend on the value of the parameter ![]() of the preon confinement which is unknown today well. At the temperatures
of the preon confinement which is unknown today well. At the temperatures ![]() in the familon gas, which is mostly in the high-symmetry phase, there begin to emerge seeds of the low-symmetry phase. However, these seeds are unstable up to the phase equilibrium temperature
in the familon gas, which is mostly in the high-symmetry phase, there begin to emerge seeds of the low-symmetry phase. However, these seeds are unstable up to the phase equilibrium temperature![]() . We also note that the spontaneous birth and death of the seeds in this temperature range is the process of density inhomogeneities generation (a certain fractality) whose development should lead to a developing gravitational instability of dark matter. The familon gas is becoming much stronger structured in the temperature range
. We also note that the spontaneous birth and death of the seeds in this temperature range is the process of density inhomogeneities generation (a certain fractality) whose development should lead to a developing gravitational instability of dark matter. The familon gas is becoming much stronger structured in the temperature range![]() . Here the seeds of the low-symmetry phase are stable, and they coexist with the remnants of the high-symmetry phase in the regime of a strong density contrast. Thus, in the domain of a relativistic phase transition in the familon gas, there happen catastrophic phenomena, one of whose consequences is a temporal coexistence of a block-phase structure, i.e., a spatial interchange of domains with high- and low-symmetry phases. From general considerations it is clear that the characteristic scale of such a structure is determined by the distance from the horizon by the time of the relativistic phase transition. It is this scale that determines the characteristic size in the baryonic subsystem structure which gravitationally responds to the dark matter structuring. Taking into account the heterogeneity of the familon gas (the existence of three familon subsystems), one can assume that the above-described phenomenon is repeated in the Universe at least three times at different temperatures of the familon gas, i.e., at different sizes of the horizon. Thus, one can expect that the suggested mechanism of dark matter structuring will enable us to elucidate the origin of the scale hierarchy in the baryon component. Besides, a fractality in the distribution of the baryon subsystem is a natural phenomenon here.
. Here the seeds of the low-symmetry phase are stable, and they coexist with the remnants of the high-symmetry phase in the regime of a strong density contrast. Thus, in the domain of a relativistic phase transition in the familon gas, there happen catastrophic phenomena, one of whose consequences is a temporal coexistence of a block-phase structure, i.e., a spatial interchange of domains with high- and low-symmetry phases. From general considerations it is clear that the characteristic scale of such a structure is determined by the distance from the horizon by the time of the relativistic phase transition. It is this scale that determines the characteristic size in the baryonic subsystem structure which gravitationally responds to the dark matter structuring. Taking into account the heterogeneity of the familon gas (the existence of three familon subsystems), one can assume that the above-described phenomenon is repeated in the Universe at least three times at different temperatures of the familon gas, i.e., at different sizes of the horizon. Thus, one can expect that the suggested mechanism of dark matter structuring will enable us to elucidate the origin of the scale hierarchy in the baryon component. Besides, a fractality in the distribution of the baryon subsystem is a natural phenomenon here.
5. Summary
Thus, the suggested model is unambiguously connected with the preon model of elementary particles which has a nice perspective of experimental verification at the colliders. No doubt that this model can be given an experimental status only after the discovery of familons. Authors [21] discussed already a possible search for composite quarks, leptons and gauge bosons on the basis of studying the dimuon mode in pp collisions at the LHC (the CMS detector). After acquiring the experimental status, adoption of this model in cosmology will be inevitable. Its advantages are already clear: it clarifies the role of particle generations in the Universe. For the very opportunity of structuring of the Universe at least three generations of particles are necessary (the first generation gives the observable baryon world, the second and third generations (their existence) give all dark matter). In this model, the second and third generations are excitations of the first generation. The “weak” place of the preon model is a lepto-boson condensate which is only mentioned and which is unknown till now in contrast to the quark-gluon condensate. Only in the preon model of elementary particles the fractality in the distribution of material components of the Universe is a natural phenomenon caused by phase transitions. In general, fractality extends the notion of homogeneity, which, from the mathematical simplicity considerations, has become a basis for cosmology of the 20th century. If proved, a fractality of the large-scale structure can lead to unexpected consequences, and who knows: can we not expect a radical revision of the standard cosmological model? However, unfortunately, for the moment there is no good proof of a fractality [22] -[24] . Indications of a fractality have been recently found in the gamma bursts distribution by scientists from Saint-Petersburg University, but so far there is not publication. There also emerges one more question since the fractality may be a “trace” of fractional extra dimensions, but it is so far practically impossible to give an answer. In any case, further studies are necessary, including both a proof of the preon model and a study of fractality in cosmology. And there certainly remains the necessity of verifying the familon composition of dark matter, although it is not an easy task. Besides, in the preon model 3 “distinguished scales” for material component (baryons and dark matter) in the Universe (galaxies, cluster of galaxies and super-clusters of galaxies) may have the natural explanation.
A part of this article was carried out 10 years ago by our team [17] [20] . The key person in these researches was G. Vereshkov.